ГДЗ Алгебра 11 клас Мерзляк
підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Завантажити (скачать) відповіді: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
КР №6. Тема. Інтеграл та його застосування
Варіант 2
Приклад 1. Обчисліть інтеграл:
1) 
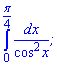
Розв'язання: Інтеграл від одиниці розділеної на косинус квадрат рівний тангенсу, тому залишається підставити межі інтегрування
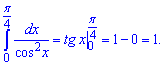
В результаті інтегрування отримали одиницю.
2) 
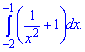
Розв'язання: Записуємо перший доданок у вигляді показникової функції та інтегруємо
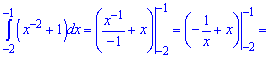
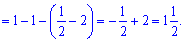
Як бачите, нічого надзвичайного в інтегруванні немає, головне знати правила.
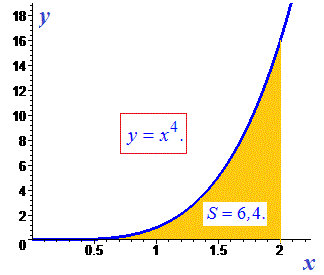
Приклад 2. Знайдіть площу фігури, обмеженої графіком функції у = х4 та прямими у = 0, х =2.
Розв'язання: Зобразимо функції на графіку
Щоб знайти межу інтегрування прирівняємо функції
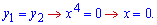
Площу знаходимо інтегруванням різниці функцій
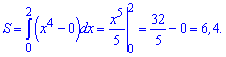
Площа рівна 6,4 одиниці квадратні.
Приклад 3. Знайдіть для функції
f(x)=5x^4+3x^2-7
первісну, графік якої проходить через точку А (1; - 4).
Розв'язання: Знаходимо первісну функції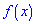 
інтегруванням
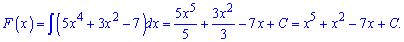
В формулу первісної входить невідома C, яку знаходимо з умови проходження первісної через точку А (1; - 4).
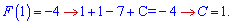
Підставляємо знайдену сталу у рівняння первісної
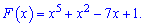
Приклад 4. Обчисліть інтеграл:
1) 
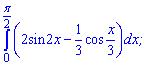
Розв'язання: При інтегруванні слід враховувати, що функції є складеними
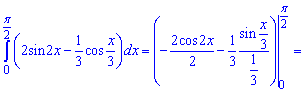
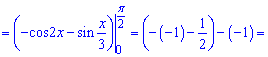
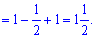
Решта обчислень зводиться до знання синусів та косинусів.
2) 
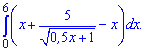
Розв'язання: Легко помітити, що 2 доданки скорочуються. Можливо в авторів невелика помилка у завданні. Представимо корінь у знаменнику через показникові функцію та візьмемо інтеграл
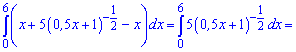
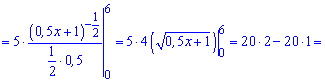
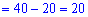
Ітеграл рівний 20.
Приклад 5. Знайдіть площу фігури, обмеженої графіком функції y=x^2+1 та прямою у = х + 3.
Розв'язання: Для наочності намалюємо обидві криві
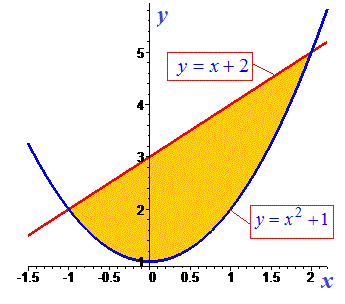
Бачимо, що пряма знаходиться вище параболи. Знаходимо точки перетину кривих
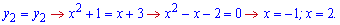
Від верхньої кривої віднімаємо нижню та знаходимо площу інтегруванням
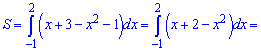
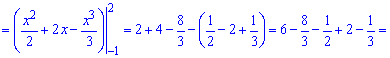
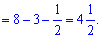
Площа рівна 4,5 одиниці квадратні.
Приклад 6. Використовуючи геометричний зміст інтегралу, обчисліть
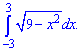
Розв'язання: Запишемо корінь у вигляді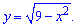 
Зведемо функцію до канонічного вигляду, для цього піднесемо її до квадрату
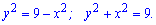
Це рівняння кола з центром в (0;0), і радіусом R=3. Його площа рівна
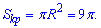
Нас цікавить тільки площа верхньої половини, тому знайдене значення ділимо на два
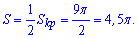
Графік функції та заштрихованої площі наведено нижче.
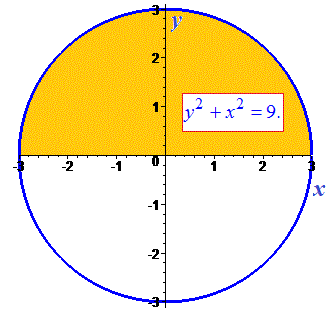
Площа рівна 4,5*Pi одиниці квадратні.
Відповідь: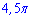 
.
На цьому типова контрольна робота для одинадцятих класів розв'язана. Вибирайте цікавий для себе матеріал та аналізуйте.
Переглянути контрольну роботу
