підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Завантажити (скачать) відповіді: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
КР № 2. Тема: Застосування похідної
1 Варіант
Приклад 1. Знайдіть проміжки зростання і спадання та точки екстремуму функції:
1)f(x)=x3-x2-5x-3
Розв'язання: Областю визначення функції є множина дійсних чисел D(f)=R.
Обчислюємо похідну функції
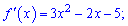
та з умови рівності нулю похідної визначаємо критичні точки
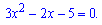
Дискримінант прийме значення
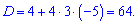
Обчислюємо корені квадратного рівняння
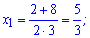
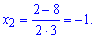
Перевіряємо знак похідної підстановкою
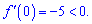
Похідна менша нуля між коренями, отже на цьому проміжку
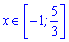
функція спадає, а за його межами зростає
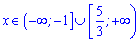 .
.
Відповідно в першому корені функція досягає локального максимуму, а в другому – мінімуму.
Ординату точок екстремуму обчислюємо підстановкою абсциси у функцію
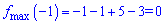
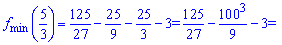
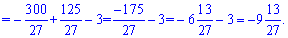
Знайшли точку максимуму 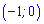 та точку мінімуму
та точку мінімуму 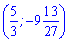 .
.
Графік функції наведено нижче
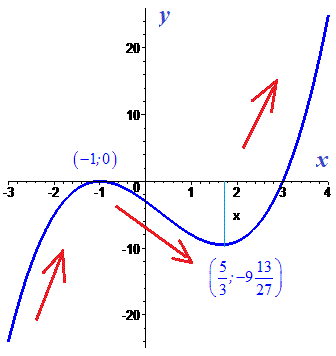
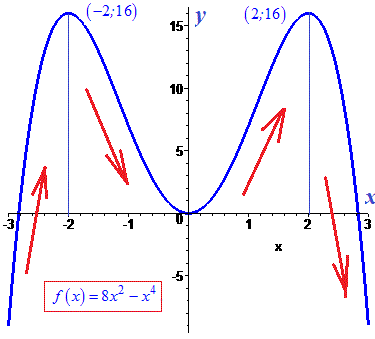
2)f(x)=8x2-x4
Розв'язання: Областю визначення є вся дійсна множина - D(f)=R.
Обчислюємо похідну функції
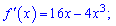
та прирівнюємо її до нуля
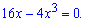
Отримали кубічне рівняння, яке вдається розділити на множники
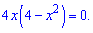
Його коренями є наступні значення
х=0; х=2; х=-2.
За знаком похідної
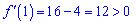
встановлюємо проміжки зростання функції
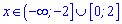
та проміжки спадання
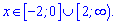
Обчислюємо ординати точок максимуму
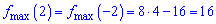
та мінімуму
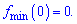
Записуємо точки максимуму (-2;16) і (2;16) та мінімуму (0;0).
Графік функції має вигляд
Приклад 2. Знайдіть найбільше і найменше значення функції
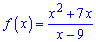
на проміжку [-4; 1].
Розв'язання: Область визначення функції обмежена знаменником
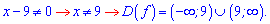
Похідна від частки прийме значення
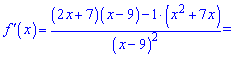
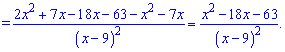
Нулі похідної знаходимо з квадратного рівняння
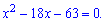
Через дискримінант
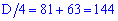
обчислюємо корені рівняння
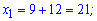
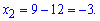
Перший корінь не належить розглядуваному проміжку
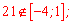
Другий підходить для обчислень
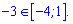
Обчислюємо значення функції в точці х=-3 і на кінцях проміжку
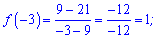
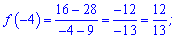
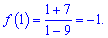
На основі знайдених значень виписуємо максимум та мінімум на проміжку
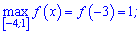
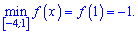
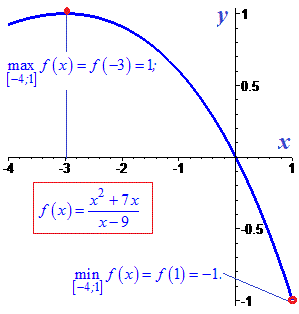
Графік функції на вказаному проміжку має вигляд
Приклад 3. Доведіть, що функція
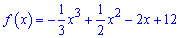 спадає на множині дійсних чисел.
спадає на множині дійсних чисел.
Розв'язання: Функція визначена на всій множині - D(f)=R.
Похідна від поліному наступна
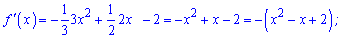
Прирівнюємо її до нуля
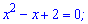
і обчислюємо дискримінант
D=1-8=-7<0.
Він менший нуля, а отже похідна або всюди додатна або від'ємна. Перевіримо знак похідної підстановкою
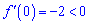
Оскільки похідна від'ємна то функція спадаюча на всій області визначення, що і треба було довести.
Графік функції має вигляд
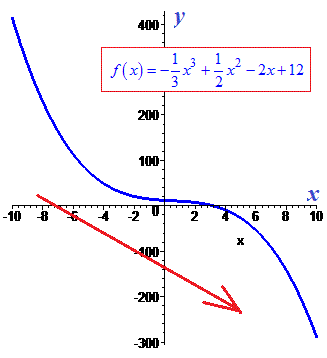
Приклад 4. Дослідіть функцію f(x)=x3-3x2 та побудуйте її графік.
Розв'язання: Функція визначена на множині дійсних чисел D(f)=R.
Перевірка на парність
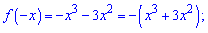
показує, що функція ні парна ні непарна.
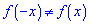 і
і 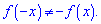
Це можна визначити і по вигляду функції, якщо вона містить тільки непарні степені то функція непарна, парні степені – парна.
Знаходимо нулі функції з кубічного рівняння
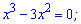
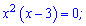
x=0; x=3- нулі функції.
Поведінку досліджуваної функції визначаємо через похідну
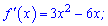
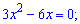
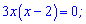
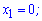
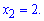
Перевіряємо знак похідної підстановкою, наприклад одиниці
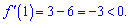
Функція зростає поза коренями 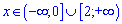 і спадає між ними [0;2].
і спадає між ними [0;2].
Обчислюємо значення функції в критичних точках
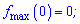
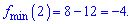
На основі виконаного аналізу проводимо побудову графіку функції.
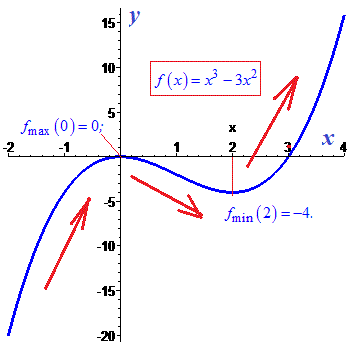
Для деталізації графіку можете обчислити значення функції в потрібних точках.
Приклад 5. Число 24 подайте у вигляді суми трьох додатних чисел так, що перше число відноситься до другого як 1:2, а сума кубів першого і другого та квадрата третього набуває найменшого значення.
Розв'язання: Позначимо перший доданок х, тоді другий - 2х,
і третій знаходимо через різницю відомих - 24-(х+2х)=24-3х.
Складемо функцію, задачу на мінімум якої потрібно розв'язати
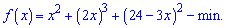
Розпишемо функцію, піднісши дужки до відповідних степенів
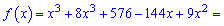
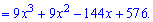
Отримали кубічну функцію, критичні точки якої визначаємо через похідну
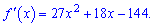
Прирівнюємо похідну до нуля
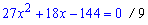
і розв'язуємо квадратне рівняння
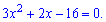
Знаходимо дискримінант
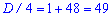
та корені
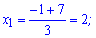
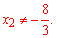
Другий корінь суперечить змісту задачі. На основі першого розраховуємо інші два числа
2x=4; 24-3x=24-6=18.
Отже, 2, 4, 18 – шукані числа.
Відповідь: 2, 4, 18.
На цьому обчислення типових прикладів даної теми завершені. Добре перегляньте схеми досліджень та цікаві Вам приклади та використовуйте здобуті знання в навчанні.
Переглянути контрольну роботу



