підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Завантажити (скачать) відповіді: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
КР №5. Тема. Елементи теорії ймовірностей і математичної статистики
Варіант ІІ
Приклад 1. Оркестру потрібні скрипаль, альтист і піаніст. На місце скрипаля є 6 кандидатів, на місце альтиста — 4, а на місце піаніста — 3. Скільки існує варіантів нового складу оркестру?
Розв'язання: Оскільки вибір кожного кандидата є подією незалежною, то новий склад оркестру можна вибрати
6*4*3=72 способами.
Мовою комбінаторики це матиме запис
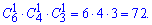
Приклад 2. У ящику лежать 8 кульок, три з яких зелені. Яка ймовірність того, що вибрані навмання три кульки будуть зеленими?
Розв'язання: Нехай подія А полягає в тому, що вибрані навмання 3 кульки будуть зеленими. Всього 8 кульок, тому першу можна вибрати трьома способами з 8. Після цього залишається 7 кульок, серед яких 2 зелені, звідси ймовірність вийняти другу зеленого кольору рівна 2/7. І наостанок, залишається одна зелена кулька серед шести, ймовірність 1/6. Оскільки кожна наступна подія можлива при виконанні попередньої, то ймовірність витягнути усі три зелені кульки рівна добутку ймовірностей
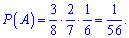
Через формули комбінаторики ймовірність рівна або
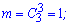
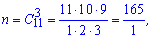
тоді
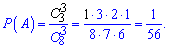
Відповідь: 1/56.
Приклад 3. Дано вибірку: 4; 7; 3; 9; 7; 5; 6; 7; 3; 8. Знайдіть її моду, медіану і середнє значення.
Розв'язання: Упорядкуємо вибірку 3;3;4;5;6;7;7;7;8;9. Мода рівна найбільш частотному значенню у вибірці. В заданому прикладі 7 зустрічається тричі, 3 двічі, тому мода рівна 7.
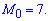
Медіана розбиває кількість елементів вибірки на рівні частини. Але в нас є 10 елементів, тому обчислюємо середнє арифметичне п'ятого і шостого (середніх)
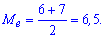
Середнє значення вибірки знаходимо за формулою
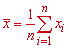
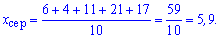
Добре запам'ятайте, як шукати ці характеристики вибірки.
Приклад 4. У коробці лежать 48 карток, пронумерованих числами від 1 до 48. Яка ймовірність того, що на навмання взятій картці буде записано число, яке:
1) кратне 6;
2) не кратне ні числу 4, ні числу 3?
Розв'язання:
1) Випишемо числа, які кратні
6: 6;12;18;24;30;36;42;48.
Їх всього 8 серед 48 всього, тому ймовірність рівна відношенню (1/6)
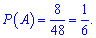
2) Записуємо усі числа, які не кратні
3 та 4: 1; 2; 5; 7; 10; 11; 13; 14; 17; 19; 22; 23; 25; 26; 29; 31; 34; 35; 37; 38; 41; 43; 46; 47.
Їх рівно половина від усіх чисел, тому і ймовірність рівна 0,5.
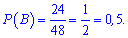
Приклад 5. У коробці лежать кульки, з яких 20 — чорні, а решта — білі. Скільки в коробці білих кульок, якщо ймовірність того, що вибрана навмання кулька виявиться білою, становить 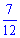 ?
?
Розв'язання: Нехай в коробці лежать х білих кульок, тоді всього 20+х, тоді ймовірність витягнути білу рівна
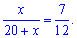
З цього відношення знаходимо кількість білих кульок
12х=140+7х; 5х=140; х=28.
Відповідь: 28 білих кульок.
Приклад 6. Скільки існує чотирицифрових чисел, усі цифри яких парні і відмінні від нуля? Розв'язання: Запишемо парні числа 2;4;6;8. Якщо можна, щоб цифри в числі повторялися то на 1, 2,3,4 місці можна поставити любу із записаних цифр. Таких чисел буде
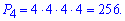
Суть Ви напевно зрозуміли.
Приклад 7. На картках написано парні числа від 2 до 16. Навмання вибирають дві з них. Яка ймовірність того, що добуток чисел, написаних на вибраних картках, є степенем двійки?
Розв'язання: Парними числами в цих межах будуть наступні
2;4;6;8;10;12;14;16.
Випишемо сприятливі добутки
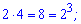
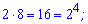

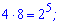
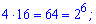
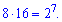
До цього запису мабуть найбільше у всіх запитань. Таких всього т=6. Загальна кількість добутків двох чисел рівна
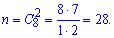
Ймовірність знаходимо через відношення значень
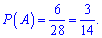
і вона рівна 3/14.
Переглянути контрольну роботу



