ГДЗ Алгебра 11 клас Мерзляк
підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Завантажити (скачать) відповіді: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
КР №3. Тема: Показникова функція. Показникові рівняння і нерівності
1 Варіант
Приклад 1. Порівняйте числа m і n, якщо:
1) 
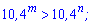
Розв'язання: При перевірці використовуйте правило: Якщо основа більша одиниці, то при розкритті нерівності знак між показниками зберігається, якщо менша одиниці – знак змінюємо на протилежний. В даному завданні основа більша одиниці тому відповідь наступна m>n
2) 
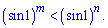
Розв'язання: Одиниця в радіанах це фактично1/3.14 частинка від Pi. Синус приймає значення між нулем і одиницею, а отже основа показникової нерівності менша одиниці. На основі цього знак між степенями міняємо на протилежний
Приклад 2. Розв'яжіть рівняння:
1) 
;
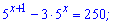Розв'язання: Розпишемо перший доданок у вигляді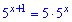 
. Тоді показникові рівняння спроститься до наступного
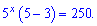
Розв'язати таке рівняння може кожен школяр
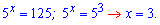
x=3 – розв'язок рівняння.
2) 
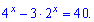
Розв'язання: Показникові рівняння заміною змінних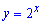 
зводимо до квадратного
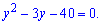
Згідно теореми Вієта розв'язки приймуть значення
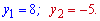
Повертаємося до заміни і визначаємо невідому
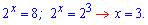
Другий корінь не має фізичного змісту, оскільки
Отже, x=3 – єдиний розв'язок показникового рівняння.
Приклад 3. Знайдіть множину розв'язків нерівності
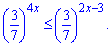
Розв'язання: Основа при показнику менша одиниці, тому при розкритті нерівності знак змінюємо на протилежний
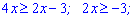
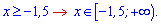
Нерівність нестрога, тому край входить в розв'язок. За цим постійно треба слідкувати.
Приклад 4. Розв'яжіть рівняння
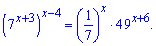
Розв'язання: Перетворюємо праву частину показникового рівняння
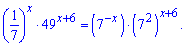
Оскільки маємо одну і ту ж основу
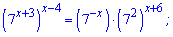
то прирівнюємо показники
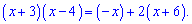
Після розкриття дужок та групування доданків отримаємо квадратне рівняння для визначення невідомих показників
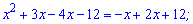
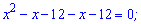
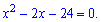
Коренями за теоремою Вієта будуть числа
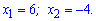
Ці два значення і є розв'язками показникового рівняння.
Приклад 5. Розв'яжіть нерівність:
1) 
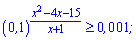
Розв'язання: Перетворимо праву сторону нерівності так, щоб справа і зліва була однакова основа
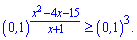
Оскільки основа 0,1<1, то знак при розкритті нерівності змінюємо на протилежний
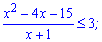
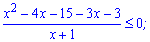
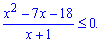
Знаходимо нулі чисельника і знаменника
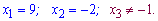
Перевіряємо знак на інтервалах підстановкою точки, для прикладу x=0
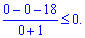
Отже на двох інтервалах
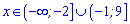
нерівність виконується
Відповідь: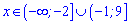 
2) 
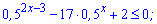
Розв'язання: Вводимо заміну змінних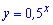 
, яка дозволить звести показникові нерівність до квадратичної
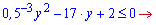
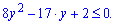
Знаходимо дискримінант
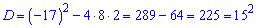
та корені рівняння
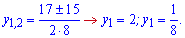
Перевіркою в нулі
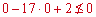
переконуємося, що нерівність виконується між коренями.
Повертаємося до заміни і визначаємо показники
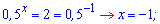
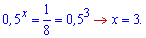
Оскільки нерівність нестрога, то розв'язком показникової нерівності буде проміжок
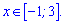
Приклад 6. Розв'яжіть рівняння
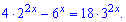
Розв'язання: Розділимо рівняння на множник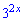 
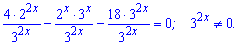
В такий спосіб вдається звести показникові рівняння до простого вигляду
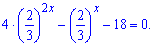
Заміною змінних
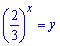
перетворюємо рівняння до квадратного
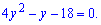
Обчислюємо дискримінант
D=1-4*4*(-18)=1+288=289
та корені
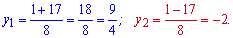
Повертаємося до заміни і визначаємо шуканий показник
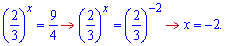
Другий корінь немає змісту розглядати, оскільки число в показнику не буває від'ємним
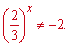
Зажди пам'ятайте про це і відсікайте зайві корені. Єдиним коренем рівняння є x=-2.
Відповідь: x=-2
На цьому ознайомлення з можливими завданнями контроьної роботи з теми "Показникові рівняння та нерівності" добігає кінця. Використовуйте даний матеріал з користю для навчання, вдосконалюйте практичний рівень обчисленням подібних завдань самостійно. Адже як не крути, а досвід приходить з пратикою.
Переглянути контрольну роботу
