ГДЗ Алгебра 11 клас Мерзляк
підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Завантажити (скачать) відповіді: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
КР №4.Тема: Логарифмічна функція. Логарифмічні рівняння і нерівності. Похідна показникової і логарифмічної функцій
1 Варіант
Приклад 1. Знайдіть область визначення функції
у = lg(4х -1).
Розв'язання: За означенням логарифма функція в дужках має бути додатною. Звідси виписуємо умову на область визначення логарифма
4х -1>0; 4х >1;x>1/4.
Область визначення складається з одного інтервалу
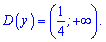
Приклад 2. Розв'яжіть рівняння:
1) 
;
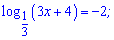Розв'язання: Розкриваємо логарифм
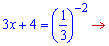
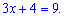
Отримали лінійне рівняння відносно невідомої. Розв'язок знайти під силу кожному
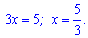
2) 
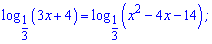
Розв'язання: Основи логарифмічного рівняння рівні, тому прирівнюємо функції в дужках.
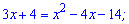
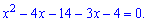
Дужки спрощуються до квадратного рівняння
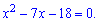
За теоремою Вієта маємо наступні корені
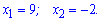
Але не спішіть виписувати у відповідь обидва корені. Досі не перевірена область визначення логарифмів. Після перевірки
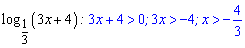
отримаємо, що лише x=9 задовільняє цю умову (є розв'язком).
Відповідь: 9.
Приклад 3. Розв'яжіть нерівність
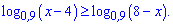
Розв'язання: Маємо нерівність в якій з двох сторін задано логарифми. Оскільки основа 0,9 < 1, то при розкритті нерівності слід змінити знак на протилежний
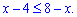
До цієї умови додаємо дві умови на область визначення логарифмів та об'єднуємо їх у систему нерівностей
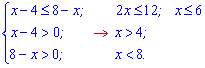
Перетином усіх інтервалів буде лише один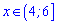 
– він і є розв'язком нерівності.
Відповідь: (4;6].
Приклад 4. Обчисліть значення виразу
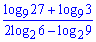
Розв'язання: Використовуючи ряд властивостей логарифма знаходимо значення виразу
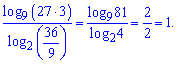
Думаю у викладенні Вам усе зрозуміле і дані властивості Ви знаєте.
Відповідь:1.
Приклад 5. Знайдіть корені рівняння:
1) 
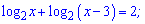
Розв'язання: ОДЗ x>3. Основи в логарифмів однакові, тому може згрупувати їх під один
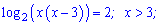
Розкриваємо логарифм і отримуємо квадратне рівняння відносно невідомої
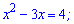
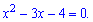
Воно достатньо просте тому корені знаходимо за теоремою Вієта
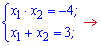
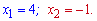
Область визначення відкидає один корінь і остаточно маємо x=4.
Відповідь: 4.
2) 
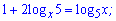
Розв'язання: За властивістю логарифма маємо дві умови
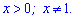
Також перетворимо один із доданків, використавши властивість логарфма
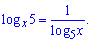
Логарифмічне рівняння перетвориться до вигляду
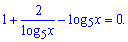
З вигляду бачимо, яку заміну слід робити
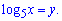
Помножимо на неї рівняння
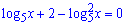
та запишемо у вигляді квадратного рівняння
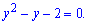
Його корені приймають значення
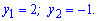
Повертаємося до заміни і знаходимо розв'язки
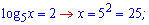
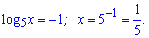
Кожен з них задовільняє наведені вище умови.
Відповідь: 25; 1/5.
Приклад 6. Розв'яжіть нерівність
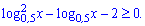
Розв'язання: Вводимо заміну змінних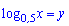 
та розв'язуємо нерівність відносно неї
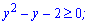
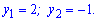
Нерівність виконується за межами знайдених коренів. Тепер повертаємоя до заміни і розписуємо дві нерівності
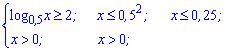
Розв'язком є два інтервали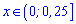 
і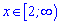 
.
Відповідь: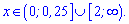 
Приклад 7. Складіть рівняння дотичної до графіка функції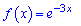 
у точці з абсцисою x0=0.
Розв'язання: Знайдемо спочатку складові рівняння дотичної. Для цього обчислимо похідну функції
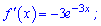
та підставимо задану точку
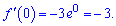
Обчислимо значення функції в точці
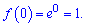
Підставляємо в формулу дотичної
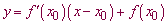
у=-3(х-0)+1=-3х+1.
Графік функції з дотичної наведено нижче
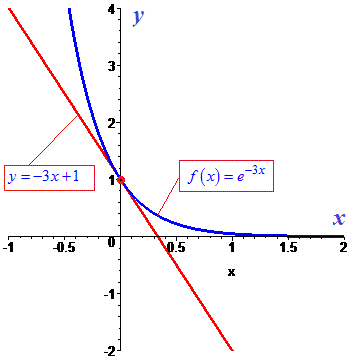
Відповідь: у=-3х+1.
Приклад 8. Побудуйте графік функції
Розв'язання: Почнемо аналіз від кореня – підкоренева функція повинна бути невід'ємною
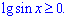
Логарифм десятковий від синуса повинен бути більший рівний нулю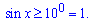 
Це можливо коли синус досягає свого максимального значення – одиниці.
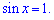
Розв'язком останнього є точки
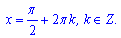
Графічно це має вигляд
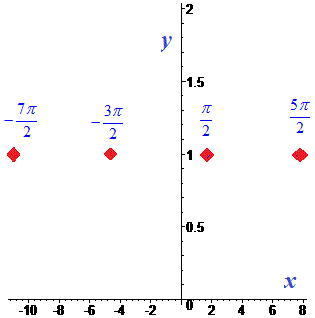
Досить проста контрольна дозволяє в короткий час перевірити знання властивостей логарифма. Добре розберіть відповіді до завдань та спробуйте подібні завдання самостійно. Це дозволить сміливо себе почувати при проходженні тестів, самостійних, ЗНО.
Переглянути контрольну роботу
