ГДЗ Алгебра 11 клас Мерзляк
підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
КР №7. Тема. Узагальнення і систематизація знань учнів
Приклад 1. Знайдіть похідну функції
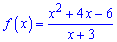
та обчисліть її значення в точці x0=-2.
Розв'язання: За правилом розписуємо похідну від частки функцій.
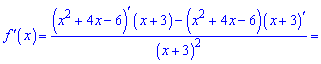
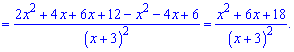
Після цього підставляємо точку
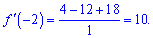
Головне в цьому прикладі і подібних – не помилитися при обчисленні похідної.
Відповідь: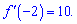 
Приклад 2. Обчисліть інтеграл:
1) 
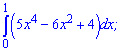
Розв'язання: Застосовуємо одну з найпростіших формул інтегрування та підставляємо межі
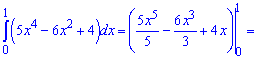
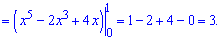
Відповідь: 3.
2) 
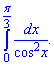
Розв'язання: Інтеграл від функції обчислюємо за табличною формулою інтегрування рівний тангенсу
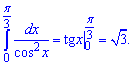
Відповідь: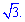 
Приклад 3. Знайдіть рівняння дотичної до графіка функції
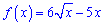
у точці з абсцисою x0=9.
Розв'язання: Обчислюємо похідну функції
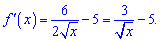
Знаходимо кутовий коефіцієнт дотичної підстановкою точки x0=9
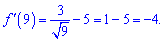
Обчислюємо значення функції в точці дотику
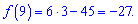
Знайдені величини підставляємо в формулу дотичної
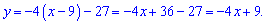
Графік функції і дотичної наведено нижче
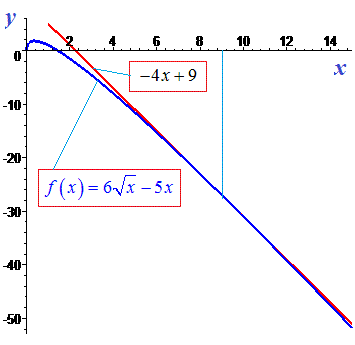
Відповідь: -4x+9.
Приклад 4. Розв'яжіть рівняння:
1) 
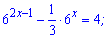
Розв'язання: Показникове рівняння записуємо у вигляді
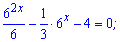
та множимо на 6 для зручності
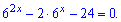
Далі вводимо заміну змінних
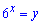
яка перетворює рівняння на квадратне
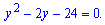
За теоремою Вієта корені рівні
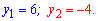
Останній відкидаємо, оскільки він не дає вкладу
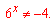
Повертаємося до заміни і знаходимо показник на основі першого кореня
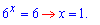
Відповідь: 1.
2) 
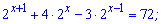
Розв'язання: Розписуємо показникове рівняння
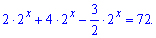
Наступним кроком виносимо множник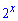 
та групуємо доданки, що залишилися
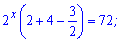
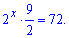
Подальші маніпуляції дозволяють швидко знайти розв'язок
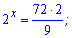
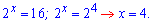
Відповідь: 4
3) 
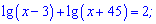
Розв'язання: Почнемо аналіз із встановлення ОДЗ логарифма
За властивістю логарифма суму перетворюємо на добуток
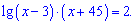
Позбуваємося логарифма в правій і лівій частинах
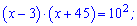
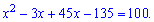
В результаті прийдемо до квадратного рівняння
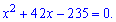
Корені обчислюємо через дискримінант
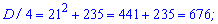
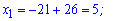
- не належить області визначення.
Отже, x=5 – єдиний розв'язок логарифмічного рівняння.
Відповідь: 5.
4) 
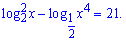
Розв'язання: Перетворимо основу в другому доданку
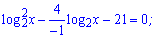
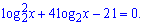
Рівняння розв'язуємо введенням нової змінної
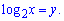
При цьому отримаємо квадратне рівняння
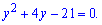
Теорема Вієта дає наступні корені
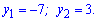
Повертаємося до заміни і визначаємо невідомі x
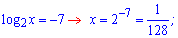
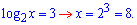
Отримали два розв'язки.
Відповідь: 1/128, 8.
Приклад 5. Розв'яжіть нерівність
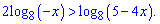
Розв'язання: Маємо логарифмічну нерівність з основою більшою одиниці (8>1). При розкритті знак нерівності зберігається + виписуємо дві умови на ОДЗ логарифма. Все це об'єднуємо в систему нерівностей
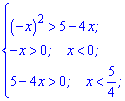
З якої встановлюємо потрібні інтервали
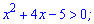
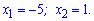
Спільним для усіх умов буде один інтервал
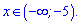
Відповідь: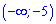 
Приклад 6. Знайдіть на інтервалі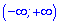 
первісну функції
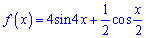
графік якої проходить через точку
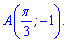
Розв'язання: Для початку знайдемо первісну функції
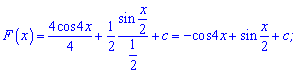
Далі з умови проходження через точку А, знаходимо невідому сталу
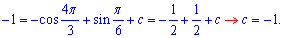
Підставляємо в формулу первісної
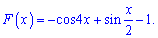
На цьому завдання виконано.
Приклад 7. Дослідіть функцію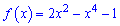 
та побудуйте її графік.
Розв'язання: Почнемо аналіз із ОДЗ -D(f)=R. Перевірка на парність
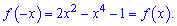
показує, що функція парна. Визначаємо нулі функції
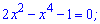
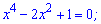
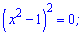
х=1; х=-1 – нулі функції.
В нуі функція рівна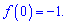
Знаходимо похідну функції
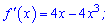
та прирівнюємо її до нуля
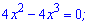
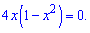
Отримаємо три точки екстремуму
х=0; х=-1; х=1.
Перевіряємо знак похідної
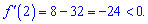
Отже функція спадає на інтервалах
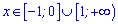
та зростає на наступних
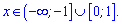
На основі цього виписуємо максимуми функції
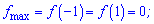
та мінімум
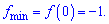
Графік функції має вигляд
Приклад 8. На чотирьох картках записано числа 3, 4, 5 і 6. Яка ймовірність того, що добуток чисел, записаних на двох навмання вибраних картках, буде парним числом?
Розв'язання: Парні добутки запишемо в ряд
3*4, 3*6, 4*5, 4*6, 5*6.
Їх всього т=5.
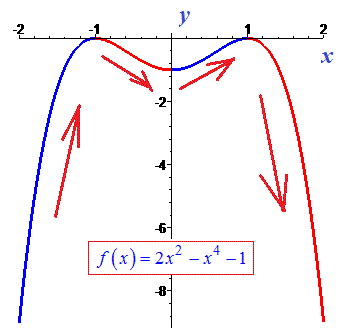
Кількість всього пар рівна
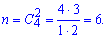
Ймовірність визначаємо через відношення кількості сприятливих пар до загальної їх кількості
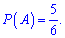
Відповідь: 5/6.
Приклад 9. Розв'яжіть нерівність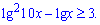 
Розв'язання: ОДЗ логарифма x>0. Перший доданок розпишемо у вигляді
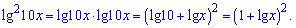
Надіюсь, що Вам усе зрозуміло в перетвореннях логарифма. Далі підставляємо у нерівність та розкриваємо дужки
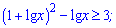
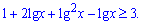
Вводимо заміну змінних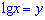 
, та переписуємо нерівність у вигляді квадратичної
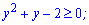
Корені рівні
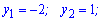
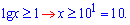
Разом з ОДЗ це дає наступні розв'язки
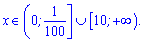
Приклад 10. При яких значеннях b і с парабола у=х^2+bx+с дотикається до прямої у = 4х +1 у точці А (1; 5)?
Розв'язання: За умовою пряма у = 4х +1 є дотичною до параболи. З цього складаємо рівняння на кутовий коефіцієнт дотичної
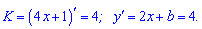
В точці А (1; 5) маємо
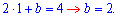
b=2;
Друга умова на значення функції
y(1)=5;
1+b+c=5;
b+c=4;
c=2.
Остаточне рівняння параболи у=х^2+2x+2.
Відповідь: b=2; c=2.
Переглянути контрольну роботу
