ГДЗ Алгебра 11 клас Мерзляк
підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Завантажити (скачати) відповіді (ГДЗ): Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
КР №1. Тема: Похідна. Рівняння дотичної
2 ВАРІАНТ
Приклад 1. Знайдіть похідну функції:
1) 
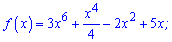
Розв'язання: Обчислюємо похідну функцію за першим правилом диференціювання
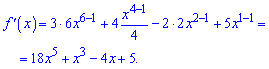
2) 
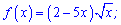
Розв'язання: Застосовуємо правило похідної від добутку функцій
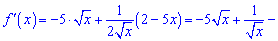
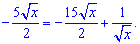
3) 
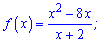
Розв'язання: Знаходимо похідну від частки функцій
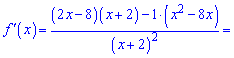
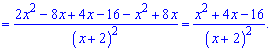
4) 
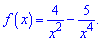
Розв'язання: Перетворимо показники до зручного вигляду
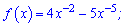
та застосуємо похідну
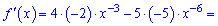
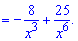
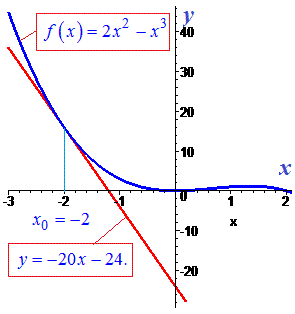
Приклад 2. Знайдіть рівняння дотичної до графіка функції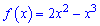 
у точці з абсцисою x0=-2
Розв'язання: Обчислюємо похідну від функції
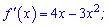
та знаходимо її значення в точці
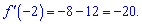
Далі обчислюємо значення функції в заданій точці
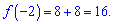
Знайдені значення підставляємо в формулу дотичної
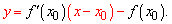
В результаті спрощень отримаємо рівняння дотичної
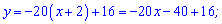
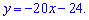
Графік функції разом із дотичною має вигляд
Приклад 3. Знайдіть похідну даної функції та обчисліть її значення в точці x0
1) 
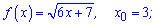
Розв'язання: Знаходимо похідну від кореневої функції. При обчисленнях враховуємо, що підкоренева функція складена
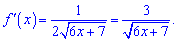
Підставляємо задану точку в похідну
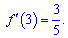
2) 
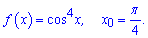
Розв'язання: Похідну від косинуса в 4 степені визначаємо за правилом складеної функції
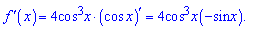
Залишилося підставити Pi/4 в похідну
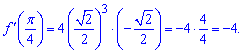
Корені спрощуються і отримуємо похідну рівну -4.
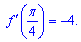
Приклад 4. Тіло рухається прямолінійно за законом
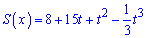
(час t вимірюється в секундах, переміщення s — у метрах). Знайдіть швидкість руху в момент часу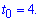 
Розв'язання: Швидкість рівна похідній від шляху
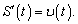
Обчислюємо похідну від закону руху
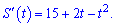
Залишається знайти швидкість в момент часу 4 секунди
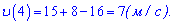
Відповідь: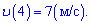 
Приклад 5. Знайдіть рівняння дотичної до графіка функції
,
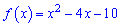яка паралельна прямій y=-6x+7.
Розв'язання: Умова паралельна прямій означає, що у прямих кутові коефіцієнти рівні між собоюь.
Знайдемо кутовий коефіцієнт дотичної
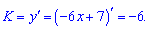
Тепер знайдемо похідну від заданої функції
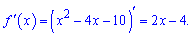
В точці дотику вона рівна K. З цієї умови знаходимо абсцису точки дотику
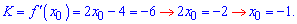
Ординату обчислюємо підстановкою
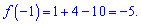
Маємо всі складові рівняння дотичної ому підставляємо їх у формулу
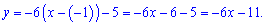
Графік функції та дотичної до неї наведено на рисунку
Відповідь: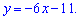 
Наведені вище розв'язки типових задач на тему "Похідна. Рівняння дотичної" стануть в нагоді школярам та студентам на самостійній, контрольній роботі, тестах. Завдання не надто складні і розібравшись в наведених обчисленнях Ви без особливих зусиль зможете розв'язати подібні приклади. Найважливіше в даному матеріалі - знати, як обчислювати похідну функції. Тож вивчайте формули похідних та вчіться їх правильно застосовувати!
Переглянути контрольну роботу
