підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Завантажити (скачать) відповіді: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
КР №6. Тема. Інтеграл та його застосування
1 Варіант
Приклад 1.Обчисліть інтеграл
1) 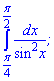
Розв'язання: Застосовуємо табличну формулу неозначеного інтегралу та підставляємо межі
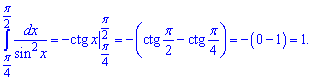
Інтеграл рівний одиниці.
2) 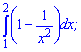
Розв'язання: Перетворимо другий доданок у дужках та виконаємо інтегрування
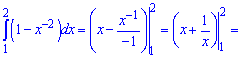
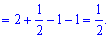
Обчислення не складні, тому Вам повинно бути все зрозумілим.
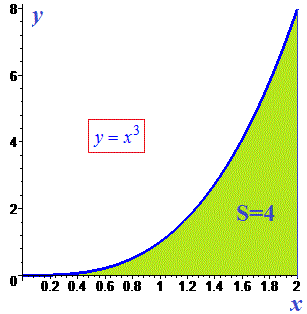
Приклад 2. Знайдіть площу фігури, обмеженої графіком функції 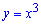 та прямими у=0 і х=2.
та прямими у=0 і х=2.
Розв'язання: Одна межа інтегрування задана і рівна х=2. Другу обчислюємо з умови перетину функцій
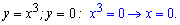
На проміжку [0;2] вище буди йти крива 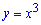 , тому від неї віднімаємо пряму та обчислюємо площу інтегруванням
, тому від неї віднімаємо пряму та обчислюємо площу інтегруванням
Графік функції із заштрихованою областю наведено нижче
Приклад 3. Знайдіть для функції 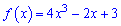 первісну, графік якої проходить через точку А (1; -2).
первісну, графік якої проходить через точку А (1; -2).
Розв'язання: Знайдемо загальний вид первісної
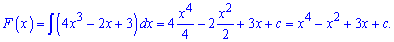
Константу С знаходимо з умови
F(1)=-2; -2=1-1+3+с; с=-5;
Підставляємо сталу у первісну
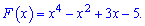
Графік первісної має вигляд
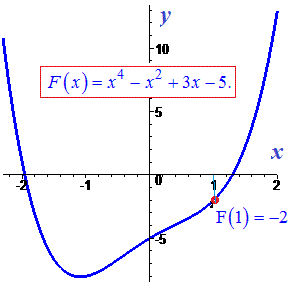
Приклад 4. Обчисліть інтеграл:
1) 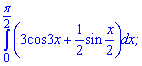
Розв'язання: Підінтегральна функція є складеною і при інтегрування виникають додаткові множники, не забувайте про них
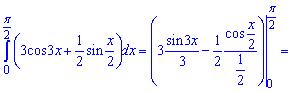
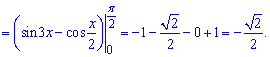
2) 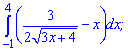
Розв'язання: Перетворимо перший доданок до зручного вигляду та інтегруємо у вказаних межах
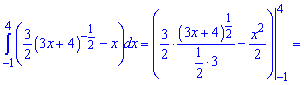
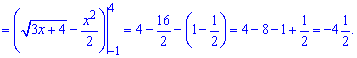
В результаті отримаємо -4,5.
Приклад 5. Знайдіть площу фігури, обмеженої графіком функції 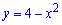 та прямою y=2-x.
та прямою y=2-x.
Розв'язання: Перша крива – це парабола з вітками донизу, друга – пряма. Площа шуканої фігури зображена нижче
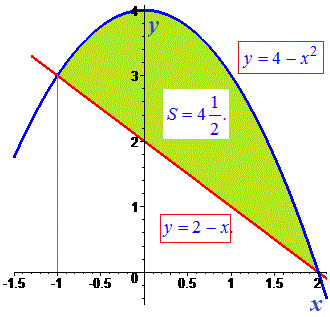
Площа рівна інтегралу від різниці функцій (від верхньої потрібно відняти нижню). Але на практиці можуть бути задані будь-які криві і, припустимо, Ви не знаєте як вони розміщені.
В першу чергу потрібно знайти точки їх перетину
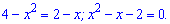
Корені квадратного рівняння за теоремою Вієта рівні 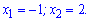
Друге завдання – з'ясувати, яка крива знаходиться вище.
На практиці це вирішується у наступний спосіб: можна підставити будь-яку зручну для обчислень точку в обидві функції і порівняти їх значення.
Візьмемо, наприклад x=0
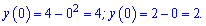
Порівнявши значення бачимо, що парабола проходить вище прямої.
Але і це немає потреби робити, пам'ятайте, що площа за фізичним змістом величина додатна і при інтегруванні, якщо отримали від'ємне число – беріть його за модулем. Від верхньої кривої віднімаємо нижню та інтегруємо
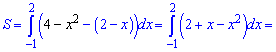
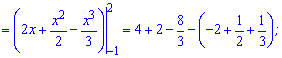
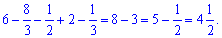
Якщо б від нижньої кривої віднімати верхню та інтегрувати, то інтеграл міняє знак на протилежний.
Площа – завжди додатна, слідкуйте за цим.
Відповідь: 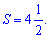
Приклад 6. Використовуючи геометричний зміст інтегралу, обчисліть
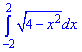
Розв'язання: Запишемо підінтегральну функцію 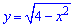 та піднесемо обидві частини до квадрату
та піднесемо обидві частини до квадрату
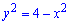 або
або 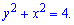
Це рівняння кола радіусом R=2.
Його площа рівна
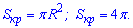
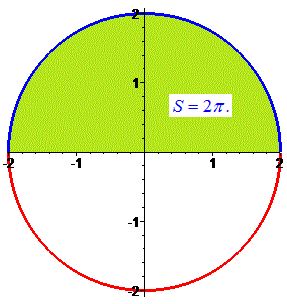
Нас же цікавить лише верхня його половина, тому знайдене значення ділимо
на 2
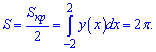
Вивчайте формули інтегрування, користуйтеся ними на практиці і подібні задачі не будуть для Вас складними при проходженні ЗНО, тестах, контрольних.
Переглянути контрольну роботу



