підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Завантажити (скачать) відповіді: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
КР №4.Тема: Логарифмічна функція. Логарифмічні рівняння і нерівності. Похідна показникової і логарифмічної функцій
Варіант 2
Приклад 1. Знайдіть область визначення функції у = lg(6 – 4x).
Розв'язання: Логарифм визначений для додатних змінних. Це накладає наступні обмеження на функцію
6-4x>0; -4x>-6;
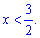
Областю визначення буде множина точок від мінус безмежності до 1,5.
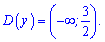
Приклад 2. Розв'яжіть рівняння:
1) 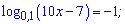
Розв'язання: Позбуваємося логарифма у рівнянні
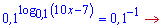
та зводимо до лінійного рівняння
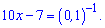
Таке рівняння розв'язати під силу кожному.
10x-7=10; 10x=17; x=1,7.
Відповідь: х=1,7.
2) 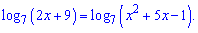
Розв'язання: Почнемо аналіз з області визначення. Функції під логарифмом повинні бути додатні
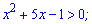
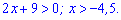
Оскільки основи логарифмів рівні між собою, то прирівнюємо функції
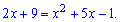
Переносимо доданки в одну сторону від знаку рівності
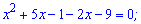
та зводимо до квадратного
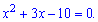
За теоремою Вієта корені рівні

Перший розв'язок відкидаємо, оскільки він не належить ОДЗ.
Відповідь: х=2.
Приклад 3. Розв'яжіть нерівність
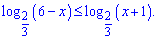
Розв'язання: Маємо логарифмічну нерівність, основи логарифмів якої менші одиниці (2/3<1 ), тому при розкритті нерівності знак змінюємо на протилежний. Крім того, функції під логарифмом мають бути додатними. Усе це записуємо в одну систему рівнянь для розв'язку нерівності
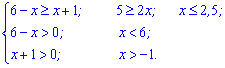
Спільним для них усіх є інтервал
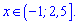
Відповідь: 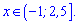
Приклад 4. Обчисліть значення виразу
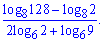
Розв'язання: Розпишемо різницю та суму логарифмів через логарифм частки та добутку. Дальше виконуємо прості спрощення
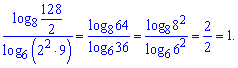
Досить цікавий приклад, який розриває найпростіші властивості логарифма.
Приклад 5. Знайдіть корені рівняння:
1) 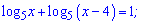
Розв'язання: Записуємо обмеження на функції в логарифмічному рівнянні
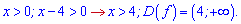
Зводимо доданки під один логарифм
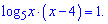
Позбуваємося логарифма
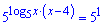
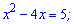
та зводимо рівняння до квадратного
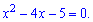
За теоремою Вієта корені рівні
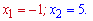
Оскільки перший корінь не належить ОДЗ, то єдиний розв'язок логарифмічного рівняння х=5.
Відповідь: 5.
2) 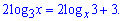
Розв'язання: Враховуючи властивість логарифма перепишемо рівняння у вигляді
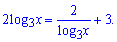
Домножимо праву і ліву частину на 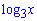
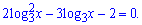
Дальше, думаю, всім зрозуміло, що необхідно виконати заміну змінних
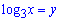
та звести рівняння до квадратного
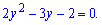
Обчислюємо дискримінант рівняння
D=9+16=25;
та корені
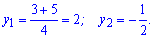
Далі необхідно повернутися до заміни та знайти невідомі x
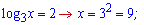
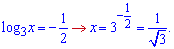
Отримали два розв'язки.
Відповідь: 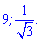
Приклад 6. Розв'яжіть нерівність
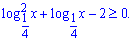
Розв'язання: Зразу виконуємо заміну змінних
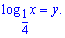
Логарифмічна нерівність перетвориться до квадратичної
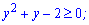
Корені рівняння -2 та 1
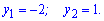
В нулі функція від'ємна, тому нерівність виконується за межами інтервалу між коренями.
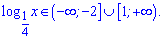
Знайдемо краї області
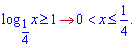
Перше обмеження на логарифм, друге –з нерівності (основа логарифма менша одиниці, знак змінюємо на протилежний).
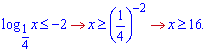
Об'єднавши двіа інтервали отримаємо наступний розв'язок.
Відповідь: 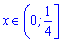 і
і 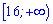
Приклад 7. Складіть рівняння дотичної до графіка функції f(х)=ln(2x+3) у точці з абсцисою х0 = -1.
Розв'язання: Обчислюємо похідну від логарифма
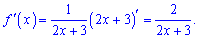
В точці дотику похідна приймає значення
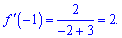
Обчислюємо функцію в цій точці
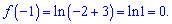
Знайдені величини підставляємо в формулу дотичної
y=2*(x+1)+0=2x+2.
Графік функції разом із дотичною наведено нижче.
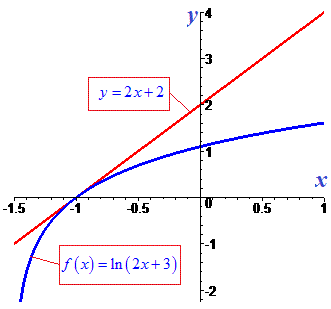
Приклад 8. Побудуйте графік функції 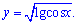
Розв'язання: Подібного роду приклади слід добре проаналізувати. Функція під коренем повинна бути додатною

Логарифм є більший рівний за нуль при змінній більшій одиниці

Оскільки косинус приймає максимум при 0 градусів, який рівний одиниці то слід розв'язувати рівняння
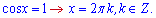
Графік функції зображено на рисунку
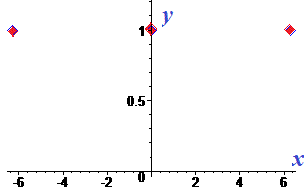
Завдання не надто складні і дозволяють перевірити уміння школярів на практиці. Без знання властивостей логарифма Ви не зможете розв'язати складніших завдань, тож вчіть їх та використовуйте. Тільки тоді тести, ЗНО і подібні перевірки не будуть Вам на заваді.
Переглянути контрольну роботу



