ГДЗ Алгебра 11 клас Мерзляк
підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
КР №3. Тема: Показникова функція. Показникові рівняння і нерівності
Варіант 2
Приклад 1. Порівняйте числа а і b, якщо:
1) 
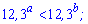
Розв'язання: За властивістю показників, при основах більше одиниці знак нерівності зберігається
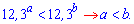
2) 
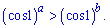
Розв'язання: Косинус 1 радіана це приблизно косинус 1/3,14*180 градусів, тобто менше 90 градусів. Відповідно косинус приймає значення менше одиниці. За властивістю показників при розкритті показникової нерівності у якої основа менша одиниці знак змінюємо на протилежний.
Отже отримаємо
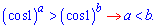
що a<b.
Приклад 2. Розв'яжіть рівняння:
1) 
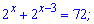
Розв'язання: Другий доданок показникового рівняння розпишемо у вигляді
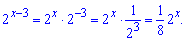
Разом із першим доданком це дозволить спростити рівняння
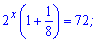
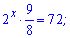
та знайти його розв'язок
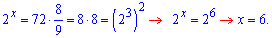
Відповідь: x=6.
2) 
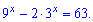
Розв'язання: Корені даного рівняння знаходять введенням заміни змінних
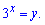
При цьому рівняння перетвориться до квадратного
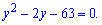
Таке рівняння розв'язувати значно простіше ніж показникові і за теоремою Вієта можемо підібрати корені
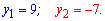
Другий зразу відкидаємо, оскільки показникові функція не може приймати від'ємні значення
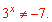
Перший корінь підставляємо у заміну та знаходимо невідомий показник
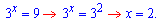
Відповідь: 2.
Приклад 3. Знайдіть множину розв'язків нерівності
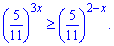
Розв'язання: Основа в показниковій нерівності менша одиниці
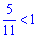
При її розкритті необхідно поміняти знак на протилежний
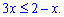
Далі виконуємо прості перетворення з нерівністю
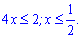
Розв'язок показникової нерівності записуємо у вигляді інтервалу
Відповідь: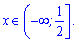 
Приклад 4. Розв'яжіть рівняння
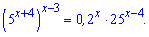
Розв'язання: Для спрощення показникового рівняння зведемо праву частину до основи 5
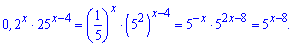
Підставимо отриманий вираз у рівняння
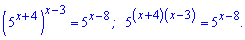
При рівних основах прирівнюємо показники
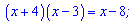
та з отриманого рівняння знаходимо розв'язки
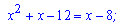
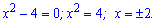
Відповідь: x=-2;x=2.
Приклад 5. Розв'яжіть нерівність:
1) 
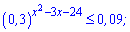
Розв'язання: Зведемо показникові нерівність до однієї основи
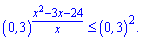
Оскільки основа менша одиниці (0,3< 1), то між показниками знак нерівності буде протилежний
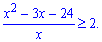
Переносимо двійку в ліву частину
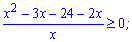
та спрощуємо до вигляду
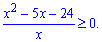
В чисельнику маємо квадратне рівняння, корені якого знаходимо за теоремою Вієта. Знаменник також вносить точку в якій функція міняє знак
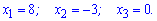
Підстановкою, наприклад одиниці, встановлюємо знаки на інтервалах
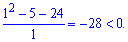
Отримали два інтервали де показникові нерівність виконується
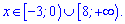
Відповідь: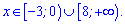 
2) 
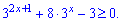
Розв'язання: Дане показникове рівняння слід розв'язувати введенням нової змінної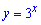 
. Перетворимо рівняння з урахуванням заміни
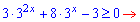
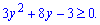
Корені квадратного рівняння знаходимо через дискримінант
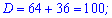
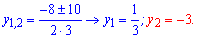
Другий корінь відкидаємо з фізичних міркувань
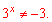
Підстановкою нуля переконуємося
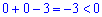
що нерівність виконується за межами коренів
Перший підставляємо у заміну і знаходимо показник
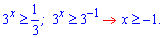
В результаті отримали, що розв'язком показникової нерівності є один інтервал
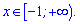
Відповідь: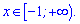 
Приклад 6. Розв'яжіть рівняння
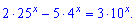
Розв'язання: Запишемо показникові рівняння після перетворень у вигляді
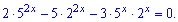
Далі слід його розділити на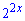 
або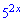 
. Кінцева відповідь від того не поміняється
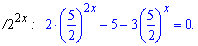
Виконаємо заміну змінних
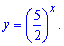
При цьому рівняння зведеться до квадратного
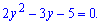
Обчислюємо дискримінант рівняння
D=9+40=49.
та корені
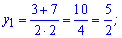
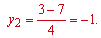
Другий корінь до уваги не беремо, тому що показникові функція не може бути від'ємною
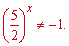
Підставимо перший корінь у заміну і знайдемо показник
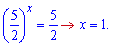
Отже x=1 – єдиний розв'язок показникового рівняння.
Ось такі приблизно приклади Вам доведеться розв'язувати на контрольних, самостійних роботах, тестах. Добре розберіться з методикою обчислень, вона нескладна і досить просто викладена.
Переглянути контрольну роботу
