ГДЗ Алгебра 11 клас Мерзляк
підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
КР № 2. Тема: Застосування похідної
Варіант 2
Приклад 1.Знайдіть проміжки зростання і спадання та точки екстремуму функції:
1) 
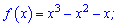
Розв'язання: ОДЗ функції вся дійсна вісь D(f)=R.
Знаходимо похідну полінома
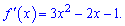
З мови рівності нулю похідної визначаємо критичні точки. Для заданої функції ця умова рівносильна квадратному рівнянню
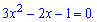
Обчислюємо дискримінант
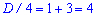
та корені квадратного рівняння
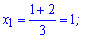
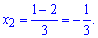
Визначаємо знак похідної підстановкою, наприклад нуля
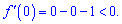
Отже функція спадає між коренями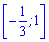 
та зростає на інтервалах 
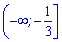і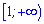 
.
Обчислимо значення функції в критичних точках
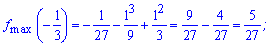
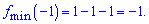
(1;-1 ) – точка мінімуму,
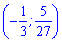- точка максимуму.
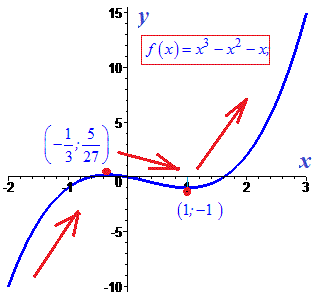
Графік функції має вигляд
2) 
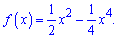
Розв'язання: Областю визначення функції є вся множина дійсних значень D(f)=R.
Знаходимо похідну функції
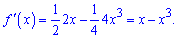
З умови рівності нулю похідної
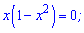
встановлюємо критичні точки
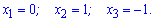
Їх всього три. Щоб встановити проміжки зростання і спадання підставляємо в похідну значення, наприклад 2
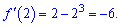
Отже на крайньому правому інтервалі функція спадна, на сусідніх інтервалах знаки функції чергуються Функція зростає на двох ділянках осі
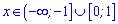
та спадає за їх межами
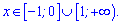
На основі цього можемо порахувати максимуми та мінімуми функції
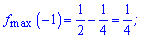
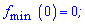
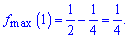
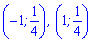- точки максимуму;
(0;0) – точка мінімуму функції.
Графік функції наведено нижче
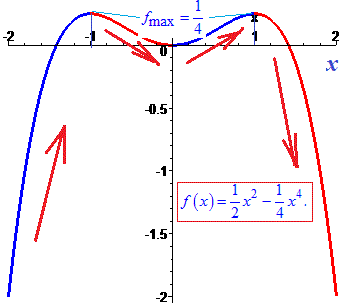
Приклад 2. Знайдіть найбільше і найменше значення функції
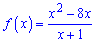
на проміжку [-5; -2].
Розв'язання: ОДЗ функція вся вісь окрім нуля знаменника
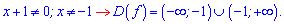
Обчислюємо похідну за правилом частки функцій
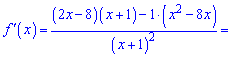
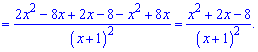
Прирівнюємо її до нуля
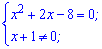
та за теоремою Вієта знаходимо корені квадратного рівняння
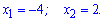
Перший із знайдених коренів належить розглядуваному проміжку, другий – ні
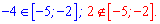
З вигляду похідної функції легко переконатися, що в нулі вона від'ємна,
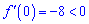
а це означає, що між коренями функція спадає і в точці x=-4 маємо локальний максимум
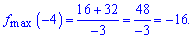
Обчислюємо значення функції на краях проміжку
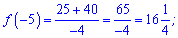
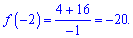
Маємо максимум та вибираємо мінімум на проміжку із знайдених тільки що значень
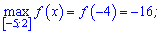
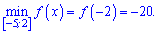
Графік функції наведено нижче
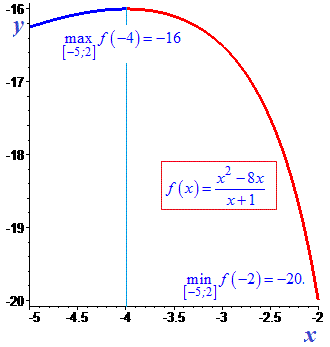
Приклад 3. Доведіть, що функція
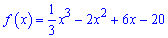
зростає на множині дійсних чисел.
Розв'язання: Функція визначена всюди. Її похідну знаходимо у вигляді
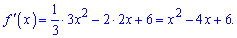
Прирівнявши похідну до нуля отримаємо квадратне рівняння для визначення критичних точок
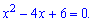
Обчислюємо дискримінант
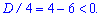
Він менший нуля, тому функція критичних точок немає. Вона або всюди зростаюча, або спадна. Встановимо це за знаком похідної, для цього підставимо нуль
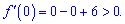
Похідна на всій області визначення додатна, а це означає, що f(x) - зростає на R.
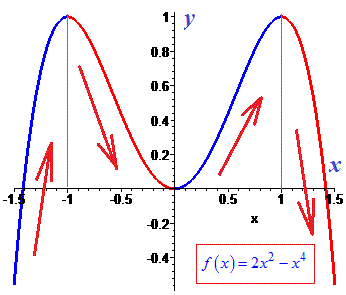
Приклад 4. Дослідіть функцію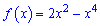 
та побудуйте її графік.
Розв'язання: ОДЗ – вся дійсна вісь D(f)=R.
Перевірка на парність показує, що функція парна
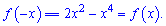
Визначимо нулі функції
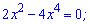
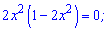
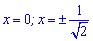- нулі функції. Знаходимо похідну функції
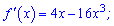
та прирівнюємо її до нуля з метою визначення критичних точок
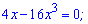
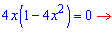
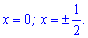
Далі за знаком похідною визначаємо проміжки зростання та спадання функції
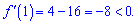
Отже на інтервалі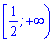 
функція спадає, на сусідніх знаки похідної чергуються. Маємо два інтервали росту функції
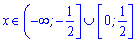
та два інтервали спадання функції
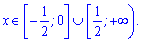
Оскільки функція парна то в максимумах матимемо однакові значення
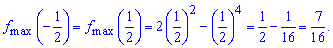
Мінімум обчислюємо досить швидко
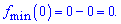
Що може бути простішим.
Графік функції наведено на рисунку
Приклад 5. Число 14 подайте у вигляді суми трьох додатних чисел так, що перше число відноситься до другого як 1:3, а сума куба першого та квадратів другого і третього набуває найменшого значення.
Розв'язання: Складемо пропорції з яких і визначатимемо невідомі числа. За умовою перше число х, друге в три рази більше - 3х, а третє рівне (14-3х-x)=14-4x.
Складемо функцію, мінімум якої необхідно знайти
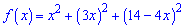
Розкладемо її в степеневий ряд
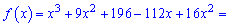
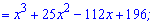
Обчислимо похідну функції
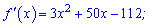
та прирівняємо її до нуля для відшукання точок екстремуму
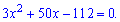
Отримане квадратне рівняння розв'язуємо через дискримінант
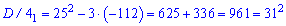
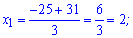
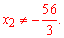
Перше число рівне х=2, тоді друге 3x=6 і третє 14-4x=6.
Дана контрольна стане Вам гарним доповненням знань, а декому, можливо, інструкцією для розв'язання задач з математики.
Переглянути контрольну роботу
