Наприклад. Закони розподілу двох випадкових величин X і Y задані таблицями:

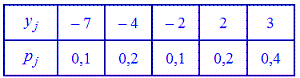
Обчислити математичне сподівання M(X) і M(Y)
Розв'язання. Знаходимо математичне сподівання за формулами
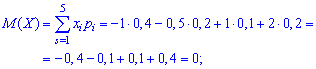
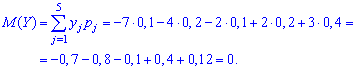
Отримали, що для двох різних законів розподілу математичні сподівання приймають однакові значення (0), при цьому можливі значення для випадкових величин X і Y різняться. Із наведеного прикладу бачимо, що в разі рівності математичних сподівань (M(X)=M(Y)=0) випадкові величини X і Y мають тенденцію до коливань відносно M(X) та M(Y) причому Y має більший розмах розсіювання відносно M(Y) порівняно з випадковою величиною X відносно M(X). Тому математичне сподівання ще називають центром розсіювання. Для визначення розсіювання вводиться числова характеристика, яку називають дисперсією.
Для визначення дисперсії розглядається відхилення випадкової величини X від свого математичного сподівання
(X-M(X))
Математичне сподівання такого відхилення випадкової величини X завжди дорівнює нулю. В цьому легко переконатися із наступного співвідношення
M(X-M(X))=M(X)-M(M(X))=M(X)-M(X)=0
Таки чином, відхилення не може бути мірою розсіювання випадкової величини.
Дисперсією випадкової величини X називають математичне сподівання квадрата відхилення випадкової величини X від свого математичного сподівання (X-M(X))
D(X)=M(X-M(X))2
Для дискретної випадкової величини X дисперсія обчислюється за формулою
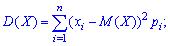
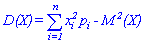
для неперервної знаходять інтегруванням
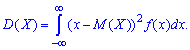
Якщо неперервна величина задана на інтервалі X∈[a,b] то дисперсія рівна інтегралу зі сталими межами інтегрування
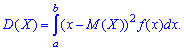
Властивості дисперсії
1. Якщо випадкова величина складається з однієї тотчки С=const — стала величина, то дисперсія рівна нулю D(C)=0.
2. Дисперсія від добутку сталої на випадкову величину рівна квадрату сталої помноженому на дисперсію випадкової величини
D(C*X)=C2D(X)
3. Якщо A і B — сталі величини, то для дисперсії D(A*X+B) справедлива залежність
D(A*X+B)=A2D(X)
Це випливає з двох попередніх властивостей.
Дисперсію можна обчислити за спрощеною формулою:
D(X)=M(X2)-M2(X)
яка у випадку дискретної випадкової величини X має вигляд
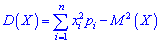
для неперервної визначається залежністю
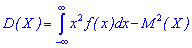
і для неперервної на проміжку X∈[a,b] співвідношенням
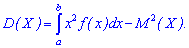
Наведені формули дуже зручні в обчисленнях, і їх, на відміну від попередніх, використовують в навчанні
Також слід пам'ятати, що дисперсія завжди приймає невід'ємні значення D(X≥0). Вона характеризує розсіювання випадкової величини відносно свого математичного сподівання. Якщо випадкова величина виміряна в деяких одиницях, то дисперсія вимірюватиметься в цих самих одиницях, але в квадраті.
Для порівняння зручно зручно користуватися числовими характеристиками однакової розмірності з випадковою величиною. Для цього вводять в розгляд середнє квадратичне відхилення – корінь квадратний із дисперсії. Її позначають грецькою літерою «сігма»
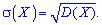
Розглянемо приклади для ознайомлення з практичною стороною визначення цих величин.
Приклади обчислення дисперсії та середнього квадратичного відхилення
Приклад 1. Закон розподілу дискретної випадкової величини X задано таблицею: Обчислити дисперсію D(X) та середнє квадратичне відхилення
Обчислити дисперсію D(X) та середнє квадратичне відхилення 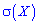 .
.
Розв'язання. Згідно з властивостями дисперсії знаходимо
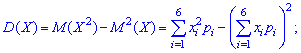
Математичне сподівання обчислюємо за формулою
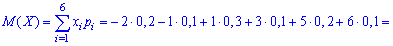
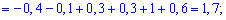
Далі знаходимо M(X2)
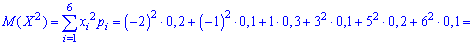
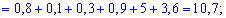
та дисперсію
D(X)=10,7-(1,7)2=10,7-2,89=7,81
Середнє квадратичне відхилення рівне ореню з дисперсії
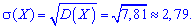
На цьому обчислення завершені і Ви можете переконатися, що знаходження імовірнісних характеристик на практиці доволі просто реалізувати. Кому важко все це рахувати вручну, можна написати програмку в Exel, Pascal. З однієї сторони не важко, з другої - один раз зробии і постійно користуєтеся.
Приклад 2. Маємо чотири електричні лампочки, кожна з яких має дефект з імовірністю q=0,2 (p=1-q=0,8 — імовірність того, що лампочка без дефекту). Послідовно беруть по одній лампочці, вкручують у патрон і вмикають електричний струм. Під час вмикання струму лампочка може перегоріти, і її заміняють на іншу. Побудувати закон розподілу дискретної випадкової величини X — число лампочок, які будуть випробувані. Обчислити середнє квадратичне відхилення 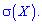
Розв'язання. Дискретна випадкова величина X — число лампочок, які будуть випробувані — набуває таких можливих значень:
x1=1, x2=2, x3=3, x4=4.
Обчислимо відповідні ймовірності:
P(X=1)=p1=0,8;
P(X=2)=p2=pq=0,16;
P(X=3)=p3=pq2=0,032;
P(X=4)=p4=pq3+q4=0,0064+0,0016=0,008.
Останню ймовірність можна трактувати наступним чином: четверта лампочка буде випробувана, коли третя перегорить, а четверта — ні, або коли й четверта перегорить.
У табличній формі закон розподілу X матиме наступний вигляд:
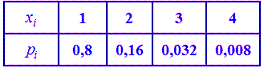
Для знаходження середнього квадратичного відхилення знайдемо спочатку значення дисперсії. Для дискретної випадкової величини знаходимо спершу математичні сподівання:
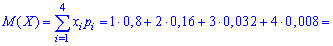
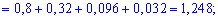
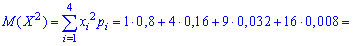
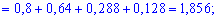
Знаходимо дисперсію випадкової величини
D(X)=M(X2)-M2(X)=1,856-(1,248)2=0,298296.
Середнє квадратичне відхилення знаходимо добуванням кореня квадратного із дисперсії.
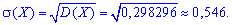
Завдання завершено встановленням усіх потрібних характеристик. Основна хитрість тут у тому, що для середнього квадратичного відхилення хоч не хоч, а потрібно шукати всі попередні величини.
Приклад 3. Закон розподілу ймовірностей дискретної випадкової величини X задано у вигляді функції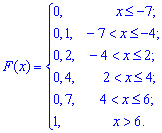 Обчислити середнє квадратичне відхилення D(X) і дисперсію σ(X).
Обчислити середнє квадратичне відхилення D(X) і дисперсію σ(X).
Розв'язання. За допомогою функції розподілу ймовірностей формуємо закон розподілу у вигляді таблиці
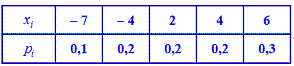
На основі таблиці розподілу обчислюємо просту медіану, медіану квадрату величини.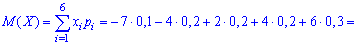
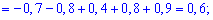
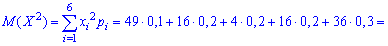
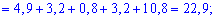
Далі знаходимо дисперсію
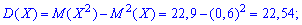
та середнє квадратичне відхилення
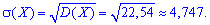
Подібних прикладів можна навести велику кількість, основна їх суть в правильному застосуванні наведених на початку статті формул для обчислення дисперсії та математичного сподівання. Застосовуйте їх там де це необхідно і не допускайте помилок при визначенні дисперсії.
]]>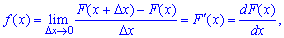
звідки диференціал 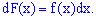
Оскільки приріст визначають залежністю
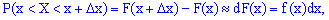
то добуток щільності ймовірностей на приріст випадкової величини f(x)dx відповідає ймовірність того, що випадкова величина X міститиметься у проміжку [x; x+dx], де dx це приріст 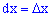 .
.
Геометрично на графіку щільності ймовірностей f(x)dx відповідає площа прямокутника з основою dx і висотою f(x)
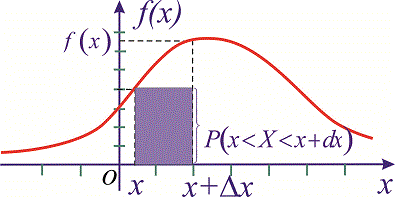
Властивості щільності ймовірностей
1. Щільність ймовірностей приймає додатні значення 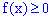 . Ця властивість випливає з означення першої похідної від функції розподілу F(x), яка в свою чергу є неспадною функцією.
. Ця властивість випливає з означення першої похідної від функції розподілу F(x), яка в свою чергу є неспадною функцією.
2. Умова нормування неперервної випадкової величини X
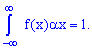
3. Імовірність попадання неперервної випадкової величини в проміжок 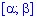 визначається залежністю
визначається залежністю
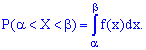
4. Функція розподілу ймовірностей неперервної випадкової величини визначається через щільність розподілу ймовірностей інтегруванням
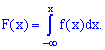
Розглянемо задачі для закріплення матеріалу на практиці.
Приклад 1. Закон розподілу неперервної випадкової величини X задано функцією
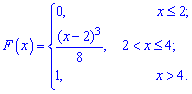
Знайти щільність розподілу ймовірностей f(x) і побудувати графіки обидвох функцій f(x), F(X). Обчислити ймовірність того, що випадкова величина належить проміжку P(2,5<X<3,5).
Розв'язання.Обчислюємо похідні від закону розподілу X
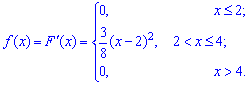
Це і буде щільність розподілу ймовірностей.
Графіки функцій f(x), F(X) зображено на рисунках
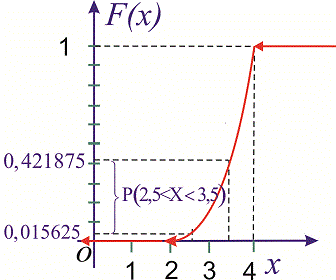
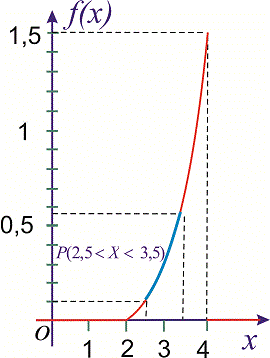
Імовірність події 2,5<X<3,5 обчислимо за формулою
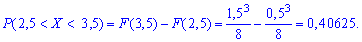
Згідно наведеної вище формули отримаємо
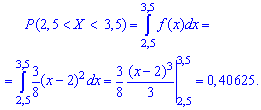
Інтегруванням щільності визначили, що ймовірність попадання веичии в проміжок рівна 0,4.
Приклад 2. За заданою функцією щільністі розподілу ймовірностей
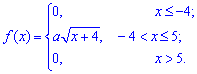
встановити параметр a та функцію розподілу ймовірностей F(x). Побудувати графіки функцій f(x), F(X).
Розв'язання. Значення сталої a визначаємо з умови нормування
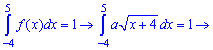
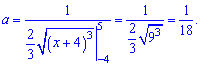
При знайденому значенні a щільність імовірностей матиме вигляд
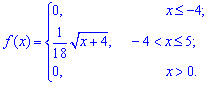
розподіл ймовірностей F(x) визначається інтегруванням щільності:

Записуємо загальний вигляд функції F(x)
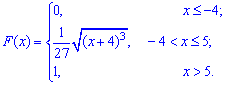
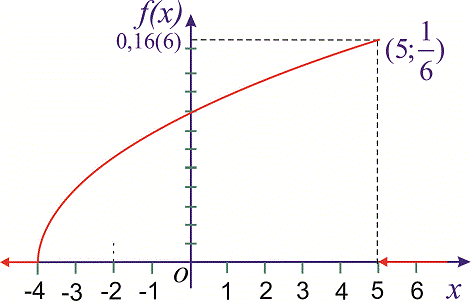
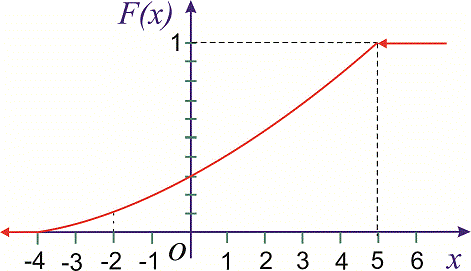
Графіки функцій розподілу ймовірностей та її щільності зображено на рисунках.
Приклад 3. Випадкова величина X має закон розподілу ймовірностей у вигляді трикутника
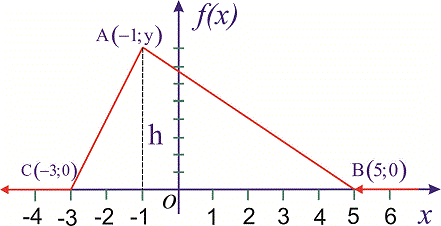
Записати вирази для щільності ймовірностей і функції розподілу ймовірностей, побудувати графік F(x) та обчислити P()<X<3).
Розв'язання. З умови завдання слідує, що щільність імовірностей на проміжках [-3;-1] та [-1;-5] змінюється за лінійним законом вигляду
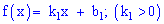
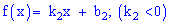
для першої та другої ділянки відповідно. Для знаходження невідомих констант 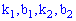 встановимо ординати вершини трикутника A(-1; y). Використаємо умову нормування, згідно з якою площа трикутника
встановимо ординати вершини трикутника A(-1; y). Використаємо умову нормування, згідно з якою площа трикутника 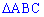 рівна одиниці:
рівна одиниці:
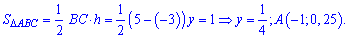
При відомих координатах усіх вершин знаходимо рівняння прямих
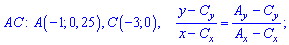
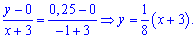
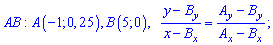
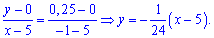
Є інший спосіб знаходження рівняння прямих, який передбачає відшукання по одній константі на рівняння. Якщо відома точка перетину прямої з віссю ординат Ox, то рівняння прямої яка через цю точку проходить наступне
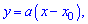
де x0 – ордината перетину з віссю Ox. Підстановкою другої точки прямої знаходять невідому константу a. Для заданих точок отримаємо
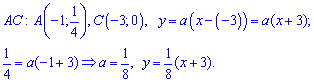
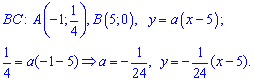
З часом другий метод для Вас стане простішим та практичнішим у використанні Щільність ймовірностей набуде значень
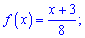
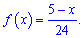
а її функція прийме вигляд
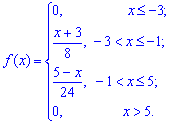
Функцію розподілу ймовірностей F(x) знаходимо інтегруванням:
а) на проміжку [-3;-1]:
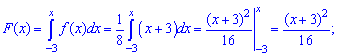
2) на проміжку [-1;5]
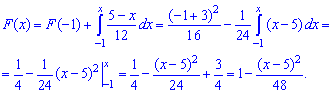
Отже, функція розподілу ймовірностей має вигляд
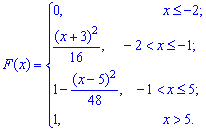
Її графік наведено нижче
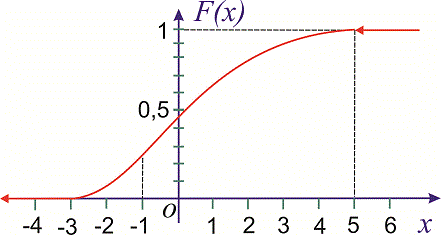
Обчислюємо ймовірність події P(0<X<3) згідно формули
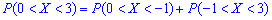
або
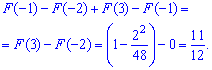
Отже, ймовірність попадання в проміжок рівна
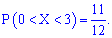
Добре проаналізуйте наведені приклади - це допоможе навчитися швидко знаходити щільність розподілу ймовірностей та виконувати побудову графіка. Будьте уважні при інтегрування та вибирайте зручну для обчислень методику.
- Вас може зацікавити:
- Щільність імовірностей f(x, y) системи двох неперервних випадкових величин
- Як знайти щільність розподілу випадкової величини?
Функція розподілу ймовірностей системи двох випадкових величин. Імовірність попадання в прямокутник - Як знайти закон розподілу та функцію розподілу випадкової величини?
- Математичне сподівання. Приклади
- Мода та медіана. Приклади обчислення
Обчислення середнього квадратичного відхилення, медіани, моди, асиметрії
Завдання 1. Побудувати статистичний розподіл вибірки, записати емпіричну функцію розподілу та обчислити такі числові характеристики:
- вибіркове середнє;
- вибіркову дисперсію;
- підправлену дисперсію;
- вибіркове середнє квадратичне відхилення;
- підправлене середнє квадратичне відхилення;
- розмах вибірки;
- медіану;
- моду;
- квантильне відхилення;
- коефіцієнт варіації;
- коефіцієнт асиметрії ;
- ексцес для вибірки:
Вибірка задана рядом 11, 9, 8, 7, 8, 11, 10, 9, 12, 7, 6, 11, 8, 7, 10, 9, 11, 8, 13, 8.
Розв'язання:
Запишемо вибірку у вигляді варіаційного ряду (у порядку зростання):
6; 7; 7; 7; 8; 8; 8; 8; 8; 9; 9; 9; 10; 10; 11; 11; 11; 11; 12; 13.
Далі записуємо статистичний розподіл вибірки у вигляді дискретного статистичного розподілу частот:
![]()
Емпіричну функцію розподілу визначатимемо за формулою
![]()
де nx – кількість елементів вибірки, що менші за х. Використовуючи таблицю і враховуючи, що обсяг вибірки рівний n=20, запишемо емпіричну функцію розподілу:

Далі обчислимо числові характеристики статистичного розподілу вибірки.
Вибіркове середнє обчислюємо за формулою
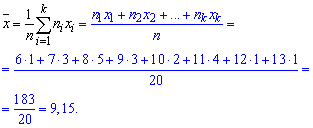
Вибіркову дисперсію знаходимо за формулою
![]()
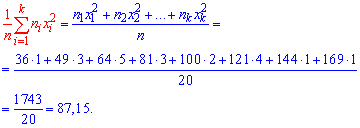
Вибіркове середнє, що фігурує в формулі у квадраті знайдено вище. Залишається все підставити у формулу
![]()
Підправлену дисперсію обчислюємо за формулою
![]()
Вибіркове середнє квадратичне відхилення обчислюємо за формулою
![]()
Підправлене середнє квадратичне відхилення обчислюємо за формулою
![]()
Розмах вибірки обчислюємо як різницю між найбільшим і найменшим значеннями її варіант, тобто:
![]()
Медіану обчислюють за формулами:
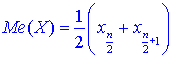 якщо число n – парне;
якщо число n – парне;
![]() якщо число п – непарне.
якщо число п – непарне.
Тут беремо індекси в xi згідно з нумерацією варіант у варіаційному ряді.
У нашому випадку п=20, тому
![]()
Мода – це варіанта, яка у варіаційному ряді трапляється найчастіше, тобто
![]()
Квантильне відхилення знаходять за формулою
![]()
де ![]() – перший квантиль,
– перший квантиль, ![]() – третій квантиль.
– третій квантиль.
Квантилі отримуємо при розбитті варіаційного ряду на 4 однакові частини.
Для заданого статистичного розподілу квантильне відхилення прийме значення
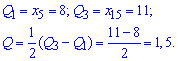
Коефіцієнт варіації рівний процентному відношенню підправленого середнього квадратичного до вибіркового середнього
![]()
Коефіцієнт асиметрії обчислюємо за формулою
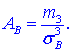
Тут m3 - центральний емпіричний момент 3-го порядку,
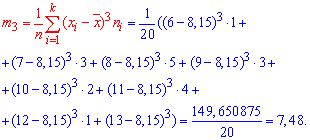
Підставляємо у формулу коефіцієнта асиметрії
![]()
Ексцесом ![]() статистичного розподілу вибірки називається число, яке обчислюється за формулою:
статистичного розподілу вибірки називається число, яке обчислюється за формулою:
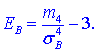
Тут m4 - центральний емпіричний момент 4-го порядку. Знаходимо момент
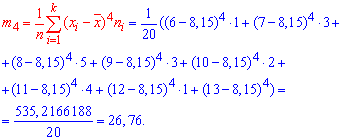
а далі ексцес
![]()
Тепер Ви маєте усі потрібні формули і знаєте, як знайти числові характеристики статистичного розподілу. Решта розв'язків індивідуальних завдань Ви знайдете в наступних матеріалах.
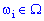 у відповідність ставиться число x або вектор
у відповідність ставиться число x або вектор 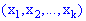 , тобто на множині
, тобто на множині  є певна функція
є певна функція 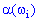 , яка для кожної елементарної події
, яка для кожної елементарної події 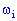 знаходить елемент одновимірного простору R1 або n - вимірного простору Rn.
знаходить елемент одновимірного простору R1 або n - вимірного простору Rn.
Цю функцію називають випадковою величиною. У випадку, коли 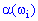 відображає множину
відображає множину  на одновимірний простір R1, випадкову величину називають одновимірною. Якщо відображення здійснюється на Rn, то випадкову величину називають n -вимірною (системою n випадкових величин або n -вимірним випадковим вектором).
на одновимірний простір R1, випадкову величину називають одновимірною. Якщо відображення здійснюється на Rn, то випадкову величину називають n -вимірною (системою n випадкових величин або n -вимірним випадковим вектором).
Величина називається випадковою, якщо внаслідок проведення досліду під впливом випадкових факторів вона набуває того чи іншого можливого числового значення з певною ймовірністю.
Якщо множина можливих значень випадкової величини є зліченною, то її називають дискретною. У протиежному випадку її називають неперервною.
Випадкові величини для зручності позначають великими літерами латинського алфавіту X, Y, Z,..., а їх можливі значення – малими x, y, z,....
Для встановлення випадкової величини необхідно знати не лише множину можливих її значень, а й вказати, з якими імовірностями вона набуває того чи іншого можливого значення.
З цією метою вводять поняття закону розподілу ймовірностей – залежність, що встановляє зв'язок між можливими значеннями випадкової величини та відповідними їм імовірностями.
Закон розподілу дискретної випадкової величини  найчастіше задають в табличній формі, функцією, або графічно за допомогою ймовірнісного многокутника.
найчастіше задають в табличній формі, функцією, або графічно за допомогою ймовірнісного многокутника.
У разі табличної форми запису закону вказується множина можливих значень випадкової величини X розміщена у порядку їх зростання в першому рядку, та відповідних їм імовірностей в наступному:
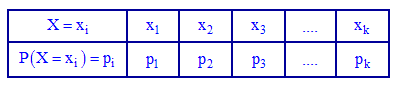
Випадкові події мають бути попарно несумісними та утворювати повну групу, тобто задовільняти умову:
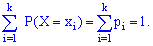
Наведену залежність називають умовою нормування для дискретної випадкової величини X, а таблицю розподілу – рядом розподілу.
Функція розподілу ймовірностей та її властивості
Закон розподілу ймовірностей можна подати у вигляді функції розподілу ймовірностей випадкової величини F(x), яка вже придатна як для дискретних, так і для неперервних випадкових величин
Функцію аргументу x, що встановлює ймовірність випадкової події X<x називають функцією розподілу ймовірностей:![]() Її слід розуміти як функцію, яка встановлює ймовірність випадкової величини, яка може приймати значення, менші за x .
Її слід розуміти як функцію, яка встановлює ймовірність випадкової величини, яка може приймати значення, менші за x .
Функція розподілу володіє наступними властивостями:
1. Вона завжди додатня із значеннями в межах від нуля до одиниці 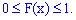
2. Функція є монотонно зростаючою, а саме значення функції зростають 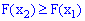 , якщо аргументи зротають x2>x1.
, якщо аргументи зротають x2>x1.
Із цієї властивості отримують наведені висновки:
a) Імовірність набуття випадковою величиною X можливих значень з проміжку  рівна приросту її інтегральної функції F(x) на цьому проміжку:
рівна приросту її інтегральної функції F(x) на цьому проміжку:
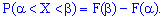 б) Імовірність, що неперервна випадкова величина X набуде конкретного можливого значення, завжди дорівнює нулю
б) Імовірність, що неперервна випадкова величина X набуде конкретного можливого значення, завжди дорівнює нулю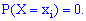 Для неперервної випадкової величини
Для неперервної випадкової величини  справджуються такі рівності:
справджуються такі рівності: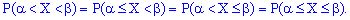 3. На крайніх точках неперервна випадкова величина приймає значення.
3. На крайніх точках неперервна випадкова величина приймає значення.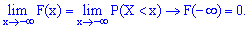
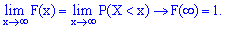
Із цих границь випливає, що для дискретної випадкової величини X з можливими значеннями з обмеженого проміжку [a;b] маємо
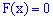 для
для 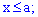
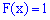 для
для 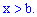
Наведемо розв'язки задач на відшукання функції розподілу.
Приклад 1. Закон розподілу дискретної випадкової величини Х задано таблицею:
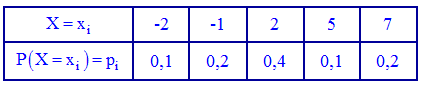
Побудувати функцію розподілу F(x) та її графік.
Розв'язання. Згідно з властивостями функції F(x) отримаємо наведені дальше значення.
1) 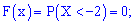
2) 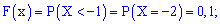
3) 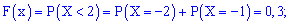
4) 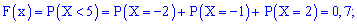
5) 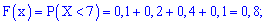
6) 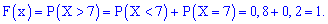
Компактно F(x) матиме запис
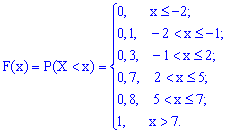
Графік функції F(x) зображено на рисунку нижче
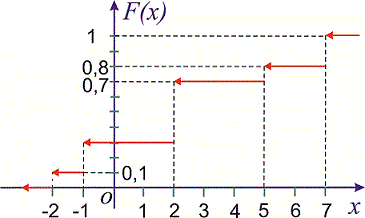
Наведений аналіз є повною відповіддю до завдання.
Приклад 2. Маємо три коробки з кульками. У першому міститься 6 жовтихих і 4 сині кульки, у другому – 7 жовтиих і 3 сині, а в третьому — 2 жовті і 8 синіх. Із кожної коробки навмання беруть по одній кульці. Побудувати закон розподілу ймовірностей дискретної випадкової величини X – появи числа синіх кульок серед трьох навмання взятих; визначити закон розподілу F(x) та побудувати графік цієї функції.
Розв'язання. Серед трьох навмання взятих кульок число синіх може бути 0; 1; 2; 3.
У табличній формі закон розподілу дискретної випадкової величини має вигляд:

Обчислимо ймовірності p1, p2, p3, p4. Із цією метою позначимо A1 випадкову подію, що полягає відповідно в появі жовтої кульки і B1 – появі синьої з першої коробки. Подібним чином для решти коробок A2, B2, A3, B3. Імовірності цих подій такі:
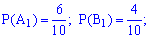
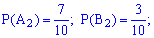
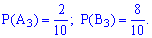
Оскільки випадкові події A1, B1, A2, B2, A3, B3 є незалежними, то ймовірності знаходимо за формулами:
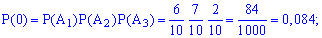
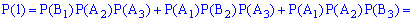
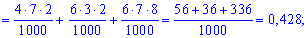
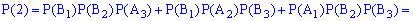
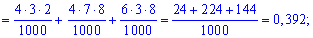
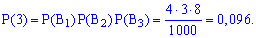
Обчислення достатньо прості і зроблені позначення повністю все пояснюють. Перевіримо виконання умови нормування
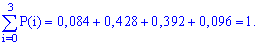
Завжди виконуйте перевірку даної умови: це достатньо просто зробити та дозволяє швидко перевірити правильність обчислень ймовірності. У випадках, коли умова нормування не виконується потрібно відшукати помилку та виправити її.
У нас же всі обчислення правильні, тому записуємо закон розподілу ймовірностей в табличній формі:
Обчислюємо значення інтегральної функції
1) 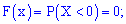
2) 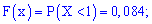
3) 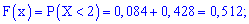
4) 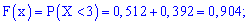
5) 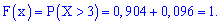
У випадку помилок при знаходженні ймовірностей останнє співвідношення дає відмінни від одиниці результат, тому можете перевіряти і за цим значенням. Спрощено функція розподілу матиме вигляд
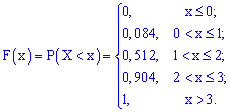
а її графік наступний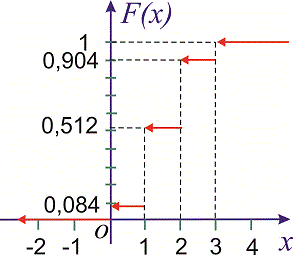
Приклад 3. Закон розподілу неперервної випадкової величини X задано функцією розподілу ймовірностей
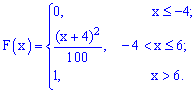
Побудувати графік функції розподілу F(X) і обчислити ймовірність, що випадкова величина належить проміжку P(1<X<4).
Розв'язання. Функція розподілу матиме вигляд.
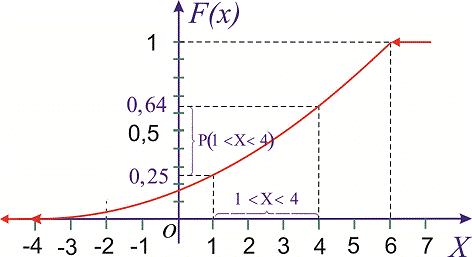
Використовуючи означення, обчислимо
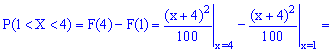
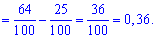
Таким чином ймовірність, що випадкова величина належить проміжку [1,4] рівна 0,36.
Уважно розберіться з наведеними прикладами знаходження функції розподілу, це Вам стане в нагоді на практичних заняттях. Старайтеся перевіряти умову нормування, щоб уникнути подальших помилок і правильно визначайте ймовірності.
- Вас може зацікавити:
- Функція розподілу ймовірностей системи двох випадкових величин. Імовірність попадання в прямокутник
- Як знайти щільність розподілу випадкової величини?
- Числові характеристики статистичного розподілу
- Як знайти закон розподілу та функцію розподілу випадкової величини?
- Математичне сподівання. Приклади
- Мода та медіана. Приклади обчислення
Приклад 4 У ящику лежать 6 виробів, з яких один виріб бракований. З ящика виймають вироби один за одним до тих пір, поки не буде вийнято бракований виріб.
Потрібно знайти:
- а) закон розподілу дискретної випадкової величини X, рівній числу вийнятих виробів;
- б) функцію розподілу випадкової величини X та побудувати її графік;
- в) математичне сподівання випадкової величини X;
- г) дисперсію і середнє квадратичне відхилення випадкової величини X;
- д) ймовірності попадання в інтервали Xє[4;5], X>5, X<4.
Розв'язання: а) Нехай X - випадкова величина, що визначає число спроб при вийняті виробів.
Оскільки у ящику 6 виробів, то X може набувати значень від 1 до 6.
Якщо перший взятий виріб буде бракований, то X=1 і P1(X)=1/6.
Якщо перший взятий виріб буде нормальним, то беремо наступний (таких виробів є 5 з 6). Якщо другий виріб буде бракованим, то число спроб буде 2, тоді
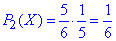
і так далі
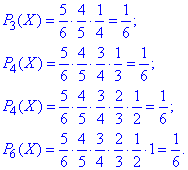
Випадкова величина X має рівномірний дискретний розподіл.
Результати запишемо в таблицю:

Графік закону розподілу має вигляд прямої
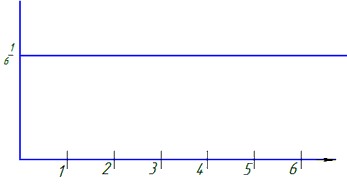
б) Функцію розподілу випадкової величини X знайдемо за формулою суми
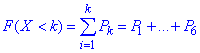
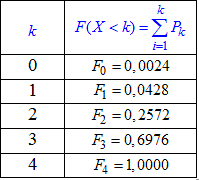
Результати запишемо в таблицю:
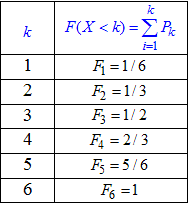
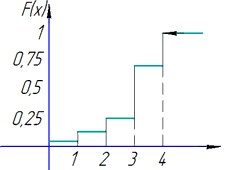
Графік функції розподілу має вигляд
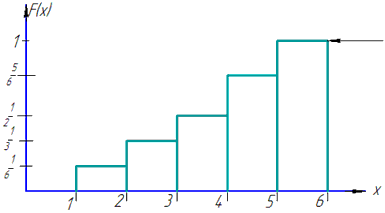
в) Математичне сподівання випадкової величини =3,5
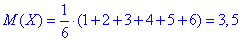
г) Дисперсія рівна 1,917
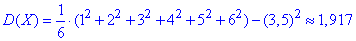
Середнє квадратичне відхилення випадкової величини X рівне 1,38:
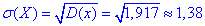
д) Ймовірності попадання в інтервали випадкової величини X
Xє[4;5] (4 або 5 разів):
p=P4+P5=1/3;
X>5 (тобто можливо лише 6 разів):
p=P6=1/6;
X<4 (від 0 до 3 разів 3*1/6):
p=P1+P2+P3=0,5
Приклад 5 Монету підкидають 11 разів.
Потрібно знайти характеристики закону розподілу, побудувати усі графіки (умови ті ж самі що і в завдання 4):
- д) ймовірності попадання в інтервали Xє[4;9], X>b, X<a.
Розв'язання: а) Оскільки від досліду до досліду ймовірність залишається сталою (а саме p=q=0.5) то ймовірність випадань герба змінюється за біноміальним законом : 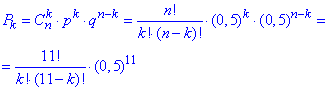
Запам'ятайте, що біноміальний розподіл найбільш поширений на практиці, на нього найбільше готових завдань.
Результати подані в таблиці:
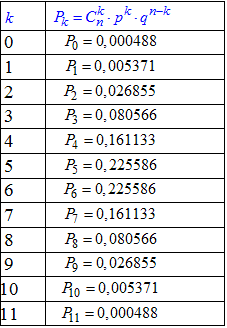
Графік закону розподілу має вигляд
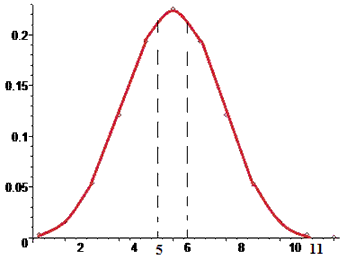
б) Функцію розподілу випадкової величини X знайдемо через формулу суми
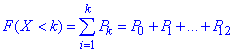
Після підрахунку отримаємо:
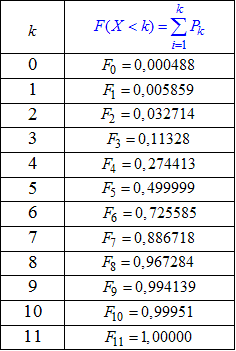
Графік функції розподілу наступний
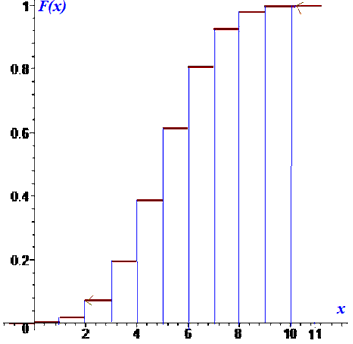
в) Знаходимо математичне сподівання випадкової величини
M(X)=n•p=11•0.5=5,5
г) Далі обчислюємо дисперсію
D(X)=n•p•q=11•0.5•0.5=2,75.
Визначаємо середнє квадратичне відхилення випадкової величини X:
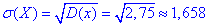
д) Ймовірності попадання в інтервали випадкової величини X наступні
Xє[4;9] (від 4 до 9 разів включно):
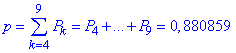
X>9 (10 або 11 разів):
p=P10+P11=0,005859
X<4 (від 0 до 3 разів - сума перших трьох значень закону розподілу):
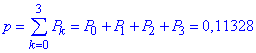
Приклад 6 В урні n=12 кульок, з яких m=3 білих, а решта чорні. З цієї урни навмання виймають k=7 кульок.
Потрібно знайти закон розподілу та побудувати його графік.
- д) ймовірності попадання в інтервали Xє[3;6], X>b, X<a.
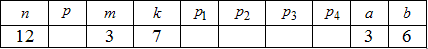
Розв'язання: а) Ймовірність Pk того, що навмання виймають l чорну кульку з 9 обчислимо за формулою (що розписана у другій задачі):
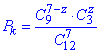
де z – кількість витягнутих білих кульок (їх не може бути більше 3),
тоді l=7-z – кількість витягнутих чорних кульок.
Випадкова величина має гіпергеометричний закон розподілу
Результати запишемо в таблицю:
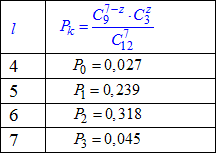
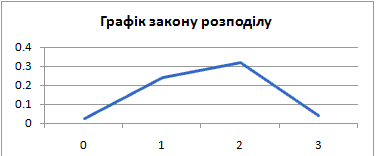
б) Функцію розподілу випадкової величини X знайдемо за формулою
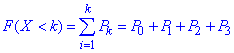
Обчислення заносимо в таблицю:
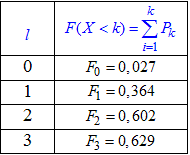
Будуємо графік функції розподілу
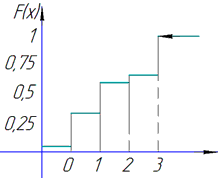
в) Обчислюємо математичне сподівання випадкової величини
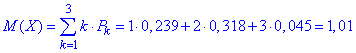
г) Знаходимо дисперсію за формулою
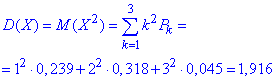
Середнє квадратичне відхилення випадкової величини X:
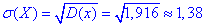
д) Ймовірності попадання в інтервали випадкової величини X
Xє[3;6] (від 3 до 6 разів включно):
p=F3=0.629;
X>6 (7 разів):
p=P0=0.027;
X<3 (0 або 1, або 2 рази), виконуємо сумування імовірностей:
p=F2=0.602
Більше готових завдань з теорії ймовірностей шукайте в даній категорії та серед відповідей до контрольних робіт.
Пам'ятайте, що наповнення сайту новими матеріалами залежить в значній мірі від Вас.
Тож діліться посиланням на корисні матеріали, надсилайте нам на пошту конспекти з практичних та замовляйте завдання!
Математичним сподіванням дискретної випадкової величини X називається величина, яка рівна сумі попарних добутків величин x[i] на їх ймовірності появи p[i]
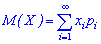 Якщо множина обмежена, то потрібно шукати суму скінченного числа доданків
Якщо множина обмежена, то потрібно шукати суму скінченного числа доданків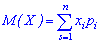 Якщо множина X є неперервною, то математичне сподіванням неперервної випадкової величини X визначається інтегруванням за формулою
Якщо множина X є неперервною, то математичне сподіванням неперервної випадкової величини X визначається інтегруванням за формулою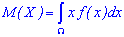 Якщо множина нескінченна
Якщо множина нескінченна 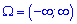 , то
, то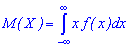
Якщо неперервна величина задана на інтервалі
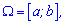 то математичне сподівання рівне
то математичне сподівання рівне 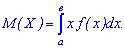
Властивості математичного сподівання
1. Математичне сподівання від сталої величини C рівне сталій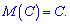 2. Сталий множник при випадковій величині можна виносити за дужки
2. Сталий множник при випадковій величині можна виносити за дужки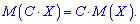 Для дискретної випадкової величини справедлива залежність
Для дискретної випадкової величини справедлива залежність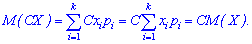 Для неперервної наступна:
Для неперервної наступна: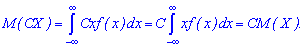 3. Якщо A і B є сталими величинами, то справедлива залежність
3. Якщо A і B є сталими величинами, то справедлива залежність
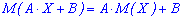
Для дискретної випадкової величини:
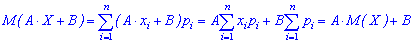
Для неперервної випадкової величини:
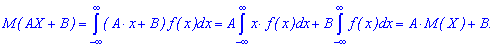
Наведемо розв'язки поширених на практиці задач.
Приклад 1. Закон розподілу дискретної випадкової величини задано таблично: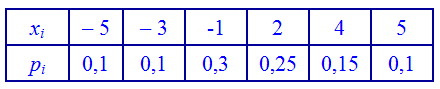 Обчислити математичне сподівання.
Обчислити математичне сподівання.
Розв'язання. Згідно наведеної вище формули, обчислюємо
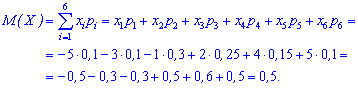
Таким чином, знайдене математичне сподівання рівне M(x)=0,5.
Приклад 2. За заданою функцією щільності ймовірностей
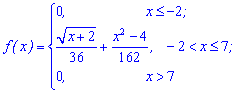
обчислити математичне сподівання.
Розв'язання. Згідно формули для неперервної випадкової величини проводимо інтегрування
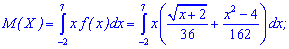
попереднто розбивши на два інтеграли
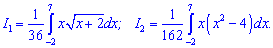
Знайдемо їх значення по черзі, для першого необхідно виконати заміну змінних
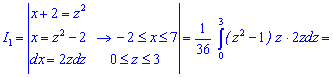
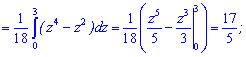
Другий інтеграл досить простий
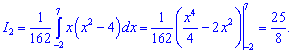
Вкінці обислюємо їх суму
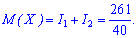
Приклад 3. Щільність імовірностей задано тригонометричною формулою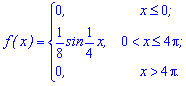 Знайти математичне сподівання.
Знайти математичне сподівання.
Розв'язання. Проводимо інтегрування частинами
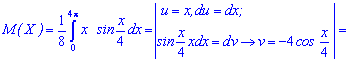
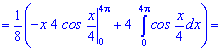
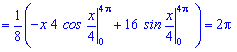
Знайдене математичне сподівання рівне 2*Pi
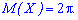
Приклад 4. За заданою функцією розподілу ймовірностей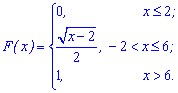 обчислити математичне сподівання.
обчислити математичне сподівання.
Розв'язання. Для обчислення M(x) необхідно спочатку знайти щільність імовірностей. Для цього здійснюємо диференціювання функції розподілу
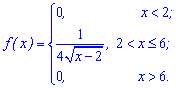
Після цього проводимо інтегрування за відомою вже формулою:
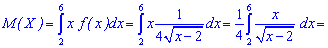
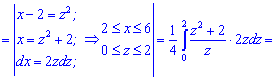
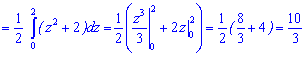
При обчисленні ітегралу довелося робити заміну змінних. Будьте в таких випадках уважними, заміна змінних у визначених інтегралах завжди приводить до зміни меж інтегрування.
Математичне сподівання рівне 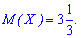
Для перевірки правильності обчислень запам'ятайте, що якщо випадкова величина належить проміжку 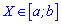 , то математичне сподівання M(x) також повинно знаходитися всередині [a; b], виконуючи роль центра розподілу цієї величини. У випадках коли знайдене математичне сподівання виходить за межі проміжку потрібно проаналізувати попередні обчислення і виправити помилки. Будьте уважними при інтегруванні функцій та заміні змінних, саме в цьому прихована левова частка Ваших помилок .
, то математичне сподівання M(x) також повинно знаходитися всередині [a; b], виконуючи роль центра розподілу цієї величини. У випадках коли знайдене математичне сподівання виходить за межі проміжку потрібно проаналізувати попередні обчислення і виправити помилки. Будьте уважними при інтегруванні функцій та заміні змінних, саме в цьому прихована левова частка Ваших помилок .
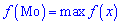
В залежності від вигляду функцію f(x) випадкова величина X може мати різну кількість мод. Якщо випадкова величина має одну моду, то такий розподіл імовірностей називають одномодальним; якщо розподіл має дві моди — двомодальним і більше – мультимодальним.
Існують і такі розподіли, які не мають моди, їх називають антимодальними. Медіаною Meнеперервної випадкової величини X називають те її значення, для якого виконуються рівність імовірностей подій, тобто щільність імовірностей справа та зліва однакові та рівні половині (0,5)
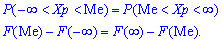
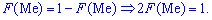
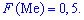 Графічно мода і медіана зображені на рисунку
Графічно мода і медіана зображені на рисунку
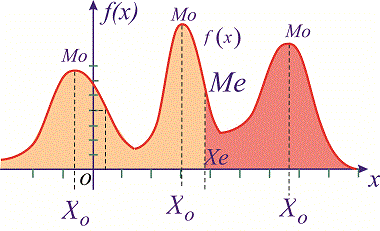
При такому значенню випадкової величини графік функції розподілу ділиться на частини з однаковою площею. Неперервна випадкова величина має лише одне значення медіани. Для дискретної випадкової величини медіану зазвичай не визначають, проте в деякій літературі наводяться правила, згідно яких, для ряду випадкових величин розміщених в порядку зростання (варіаційного ряду) моду визначають згідно розподілу: якщо маємо непарну кількість випадкових величин N=2k+1 то медіана рівна середній величині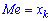 у випадку парної кількості N=2k півсумі середніх величин
у випадку парної кількості N=2k півсумі середніх величин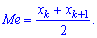 Розглянемо приклади визначення моди та медіани.
Розглянемо приклади визначення моди та медіани.
Приклад 1. В розважальному центрі працівник обслуговує чотири доріжки для боулінгу. Імовірність того, що котрась доріжка потребує прибирання протягом зміни є сталою величиною з ймовірністю 85%.
Побудувати закон розподілу ймовірностей дискретної випадкової величини X — кількість доріжок, які потребують прибирання. Знайти моду X.
Розв'язання. Випадкова величина може приймати значення
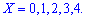
Імовірності появи значень визначаємо за твірною функцією
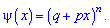
Для заданої задачі вхідні величини приймають значення
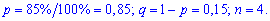
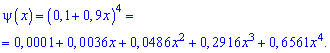
Шукані ймовірності входять множниками при степенях аргумента
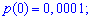
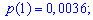
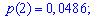
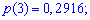
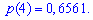
Закон розподілу ймовірностей запишемо у вигляді таблиці
Із таблиці визначаємо моду Mo=4, як значення при максимальній ймовірності. Отримали одномодальний розподіл.
Приклад 2. За заданою щільністю ймовірностей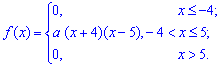 Знайти параметр a , щільність ймовірностей F(x), моду Mo.
Знайти параметр a , щільність ймовірностей F(x), моду Mo.
Розв'язання. Застосовуючи умову нормування виконуємо інтегрування щільності розподілу
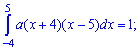
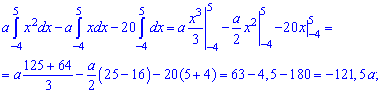
після того визначаємо параметр
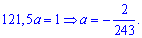
Щільність імовірностей, враховуючи знайдене значення матиме вигляд
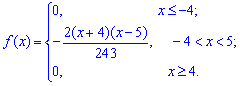
а її графік зображено на рисунку нижче
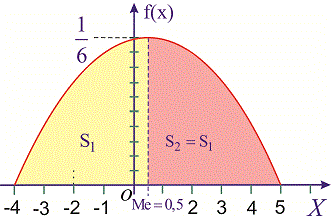
З графіка щільності ймовірностей бачимо, що мода приймає значення Mo=0,5. Визначимо медіану Me за допомогою функції розподілу ймовірностей. ЇЇ значення на проміжку [-4; 5] знаходимо інтегруванням
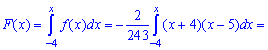
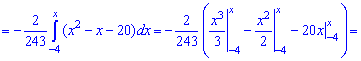
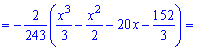
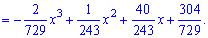
Функція розподілу матиме наступний вигляд
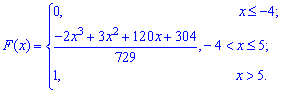
а її графік матиме вигляд
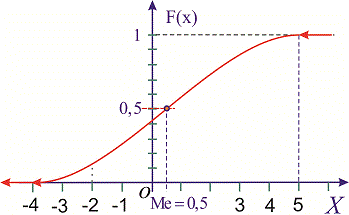
Для визначення медіани випадкової величини Me застосовуємо формулу
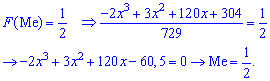
Медіану Me можна знайти за допомогою щільності ймовірностей 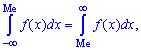 для дискретної випадкової величини з проміжку
для дискретної випадкової величини з проміжку 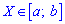
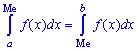 Таким чином медіану Me — можливе значення випадкової величини X, при якому пряма, що проведена перпендикулярно до відповідної точки на площині X=Me, ділить площу фігури, яка обмежена функцією щільності ймовірностей f(x) на дві рівні частини.
Таким чином медіану Me — можливе значення випадкової величини X, при якому пряма, що проведена перпендикулярно до відповідної точки на площині X=Me, ділить площу фігури, яка обмежена функцією щільності ймовірностей f(x) на дві рівні частини.
Завдання на визначення моди та медіани випадкової величини зустрічаються на практиці не так часто, як щільності розподілу ймовірностей, однак наведений вище теоретичний матеріал та розв'язки поширених прикладів допоможуть Вам знаходити ці велечини без великих затрат часу. При необхідності Ви завжди можете замовити розв'язання задач з теорії ймовірностей у нас.
ul>Вас може зацікавити:
]]>Приклад 1 В урні n=10 кульок, з яких m=5 білих, а решта чорні.
З цієї урни навмання виймають k=5 кульок.
Потрібно знайти:
- а) закон розподілу дискретної випадкової величини X, рівній числу вийнятих чорних кульок;
- б) функцію розподілу випадкової величини X та побудувати її графік;
- в) математичне сподівання випадкової величини X;
- г) дисперсію і середнє квадратичне відхилення випадкової величини X;
- д) ймовірності попадання в інтервали
 , X>b, X<a.
, X>b, X<a.

Пункти а)-г) в кожному із завдань повторюється тому їх дальше наводити не будемо.
В інтернеті можна знайти ще безліч завдань в основному на біноміальний, рівномірний та гіпергеометричний розподіли.
Розв'язання: а) Ймовірність Pk того, що навмання виймають z чорних кульок з 5 обчислимо за формулою:
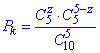
де z – кількість витягнутих чорних кульок.
Чому саме така залежність для ймовірності детально розписано в статті про кульки.
Загалом ймовірність змінюється за формулою гіпергеометричного розподілу.
Результати обчислень запишемо в таблицю:
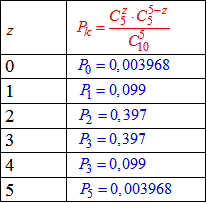
Загалом тут буде пояснено сам хід обчислень, детальні обчислення зі спрощенням факторіалів Вам мають бути знайомі.
Формули сполучень з повтореннями та без них на момент вивчення теми Вам мають бути знайомі, інакше слід починати з основ комбінаторики і переглянути базовий матеріал.
На основі таблиці закону розподілу виконуємо побудову графіка
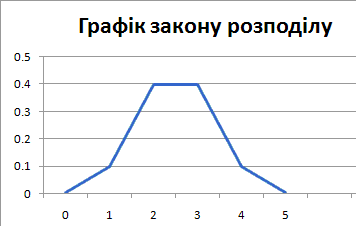
В Вас він повинен виглядати подібно, незалежно від того в чому виконуєте побудову.
б) Функцію розподілу випадкової величини X знайдемо за формулою
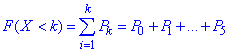
Детальніше про її властивості та фізичний зміст Ви можете ознайомитися за наведеним вище посиланням.
Для дискретно розподіленої випадкової величини функція розподілу рівна сумі попередніх ймовірностей, для неперервної випадової величини - інтегралу з верхньою обмеженою границею.
Результати запишемо в таблицю:
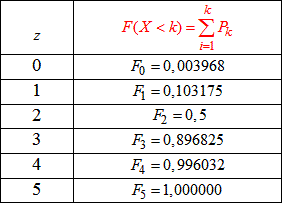
Далі будуємо графік функції розподілу
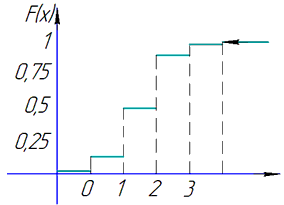
Для дискретних випадкових величин вона має вигляд "сходин". На цьому типовий приклад, який може чекати Вас на модулі чи заліку обчислено.
Переходимо до інших типових завдань на розподіли випадкових величин
Приклад 2 Ймовірність того, що витрати електроенергії на підприємстві протягом дня не будуть перевищувати норми, дорівнює p=0,9.
Нехай 8 - кількість днів, протягом яких працює підприємство, а X- кількість днів, протягом кожного з яких витрати електроенергії не будуть перевищувати норми.
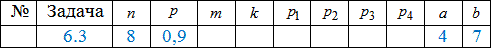
Розв'язання: а) Оскільки від досліду до досліду ймовірність залишається сталою (а саме p=0.9 і q=1-p=0.1), то ймовірність того, що витрати електроенергії на підприємстві протягом дня не будуть перевищувати норми з кожним днем знайдемо із залежності:
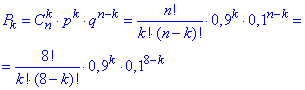
Результати запишемо в таблицю:
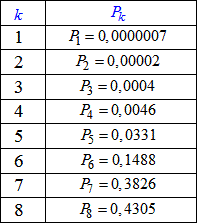
Графік закону розподілу матиме вигляд
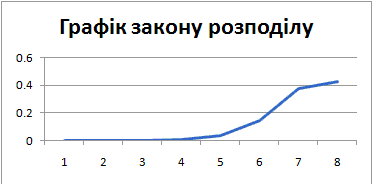
б) Функцію розподілу випадкової величини X знайдемо за формулою суми
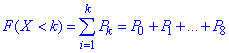
Результати сумування ймовірностей записуємо в таблицю:
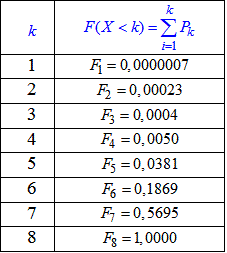
Графік функції розподілу має вигляд
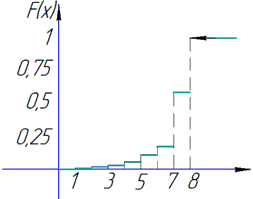
в) Математичне сподівання випадкової величини
M(X)=n•p=8•0.9=7.2
г) Дисперсія D(X)=n•p•q=8•0.9•0.1=0.72
Середнє квадратичне відхилення випадкової величини X:
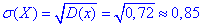
д) Ймовірності попадання в інтервали випадкової величини X
Xє[4;7] (від 4 до 7 разів включно):
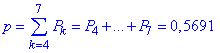
X>7 (8 разів):
p=P8=0.4305;
X<4 (від 1 до 3 разів):
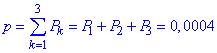
Ось і всі розрахунки входження випадкових величин в інтервали.
Приклад 3 Робітник обслуговує 4 незалежно працюючих верстати. Ймовірність того, що протягом години станок не буде потребувати уваги робітника, дорівнює для першого верстата p1=0,6, для другого – p2=0,7, для третього – p3=0,8 , для четвертого – p4=0,9. Знайти характеристики розподілу.

Розв'язання: а) Ймовірність Pk того, що протягом години кількість верстатів не буде потребувати уваги робітника, обчислюємо, як і в задачі 3, тобто таким чином pk – ймовірність, що k-й верстат не потребує уваги робітника.
qk=1-pk – ймовірність, що k-й верстат потребує уваги робітника.
P0=q1•q2•q3•q4 – для жодного верстату не треба уваги робітника;
P1=p1•q2•q3•q4+q1•p2•q3•q4+... – для одного верстату;
P2=p1•p2•q3•q4+q1•p2•p3•q4+... – для 2-х верстатів;
P3=p1•p2•p3•q4+p1•p2•q3•p4+p1•q2•p3•p4+q1•p2•p3•p4 – для 3-х верстатів;
P4=p1•p2•p3•p4 – для всіх верстатів не треба уваги робітника.
Результати обчислень запишемо в таблицю:
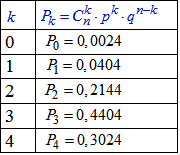
Будуємо графік закону розподілу
б) Функцію розподілу випадкової величини X знайдемо за формулою
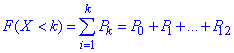
Результати сум записуємо в таблицю:
Графік функції розподілу наведено далі
в) Математичне сподівання випадкової величини 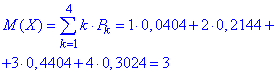
г) Дисперсія
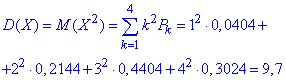
Середнє квадратичне відхилення випадкової величини X:
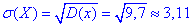
д) Ймовірності попадання в інтервали випадкової величини X
Хє[1;3] (від 1 до 3 разів включно):
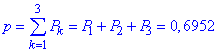
X>3 (4 рази):
p=P4=0.3024
X<1 (0 раз):
p=P0=0.0024.
Для двомірного випадку, коли маємо систему двох випадкових величин (X,Y) також встановлюють закони розподлу однєї з величин.
Завдання 3.2 Задано закон розподілу системи випадкових величин (X,Y).
|
Y \ X |
-1 |
2 |
3 |
|
-3 |
0,1 |
0,3 |
0,2 |
|
3 |
0,1 |
0,15 |
0,15 |
Знайти закон розподілу випадкової величини X.
Розв'язування: Запишемо розподіл X (pi відповідає сумі ймовірностей кожного стовпчика):
|
Y \ X |
-1 |
2 |
3 |
|
-3 |
0,1 |
0,3 |
0,2 |
|
3 |
0,1 |
0,15 |
0,15 |
Перевірка: ∑pi=0,2+0,45+0,35=1.
Як бачите завдання не складні і їх під силу вирішити кожному. Знаходження законів розподілу для неперервних випадкових величин розглянемо в наступних публікаціях, для їх відшукання Ви повинні добре вміти інтегрувати. Якщо Вам важко написати модуль чи підсумкову контрольну самостійно, то ми готові Вам допомогти! Для цього зробіть замовлення та очікуйте на відповіді з поясненнями.
]]>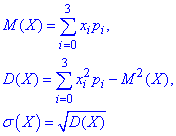
Приклад 1. Гральний кубик кидають три рази. Скласти закон розподілу випадкової величини Х – кількості появи двійки на верхній грані кубика.
Обчислити M(X), D(X) та середнє квадратичне відхилення σ.
Обчислення: Гральний кубик має 6 граней, на одній з яких 2.
Ймовірність, що випаде двійка в одному киданні рівна p1=1/6, що не випаде q1=5/6.
Закон розподілу: ймовірності, що двійка при трьох кидках випаде 0,1,2,3 рази.
p(0)=5/6^3=0,5787;
p(1)=3•1/6•5/6•5/6=0,3471;
p(2)=3•1/6•1/6•5/6=0,0693;
p(3)=1/6•1/6•1/6=0,00461.
У 2 і 3 рядках домножали на 3 за рахунок розміщень з 3 по 2 (A32=3!/2!).
Складаємо таблицю розподілу Х
|
Х |
0 |
1 |
2 |
3 |
|
p(x) |
0,5787 |
0,3471 |
0,0693 |
0,00461 |
Математичне сподівання, дисперсію та середнє квадратичне відхилення знаходимо з формул
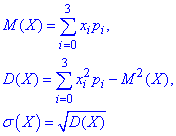
M(x)=0,5787*0+1*0,3471+2*0,0693+3*0,00461=0,01458;
D(x)=1*0,3471+4*0,0693+9*0,00461-0,01458=0,0283;
σ(X)=√D(x)=√0,0283=0,1682.
Запам'ятовуйте формули для обчислення числових характеристик дискретної випадкової величини.
Приклад 2. З дев'яти кульок, серед яких є 4 пофарбовані, навмання вибирають 5 кульок. Скласти ряд розподілу і побудувати функцію розподілу випадкової величини Х – кількості пофарбованих кульок серед вибраних.
Обчислення: Кількість пофарбованих кульок може приймати значення від 0 до їх максимальної кількості =4 серед 5, що вибирають. Оскільки "кульки" не "діти, книжки,..." і немає значення під яким номером входять в набір, а лише їх кількість то кількість всеможливих наборів визначаємо через формулу комбінацій.
Кількість різних варіантів вибрати 5 кульок з 9 рівна С95.
k – кульок з 4 пофарбованих можна вибрати С4k способами і лишається вибрати (5-k) непофарбованих з 5, що дорівнює С55-k.
Тоді за теоремою множення ймовірностей функція розподілу рівна
p(k)=С4k•С55-k/С95.
Для обчислення ймовірностей скористаємося математичним пакетом мейпл, в ньому за комбінації з n по m відповідає функція binomial(n,m).
Решта обчислень як і графік розподілу наведені нижче .

Зауважте, що в мейплі початковий номер має бути натуральним числом, тому зміщаємо в формулі індексна 1 вліво.
Результати записуємо в таблицю розподілу:
|
X |
0 |
1 |
2 |
3 |
4 |
|
P(X) |
1/126 |
10/63 |
10/21 |
10/63 |
5/126 |
На основі ряду розподілу ймовірностей побудуємо функцію ймовірностей F(x).
Спершу вручну, як вимагають на практичних для студентів
F(X<0)=0;
F(0<X<1)=p(X=0)=1/126≈0,079;
F(1<X<2)=p(X=0)+p(X=1)=21/126=0,16(6);
F(2<X<3)=1/126+10/63+10/21≈0,643;
F(3<X<4)=F(2<X<3)+p(X=3)=0,643+10/63≈0,96;
F(X>4)=1.
Далі покажемо, як обчислити функцію розподілу в мейплі та побудувати її графік.
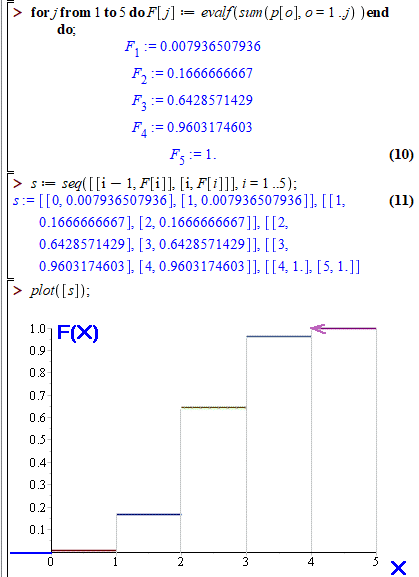
Саме такий вигляд має графік функції розподілу, іноді вимагають ставити всюди вектори як на останній ділянці.
Приклад 3. На полиці стоять 5 підручників з математики і 3 з фізики. З полиці навмання беруть три книги.
Скласти закон розподілу випадкової величини Х – кількості підручників з математики серед відібраних.
Обчислити числові характеристики M(X), D(X), σ(X).
Обчислення: Х – може приймати значення від 0 до 3. Розв'яжемо завдання двома способами.
1 спосіб
Пояснимо на пальцях усі ймовірності.
Нехай першою треба знайти ймовірність, що виберуть 0 книг з математики.
Це означає, що треба вибрати лише 3 книги з фізики з 3 серед (5+3)=8 можливих.
Ймовірність вибрати фізику першою рівна 3/8.
Після цього залишиться 8-1=7 книг, 2 з яких з фізики, тому ймовірність другою взяти фізику рівна 2/7, третьою – 1/6.
За теоремою множення ймовірностей
p(0)=3/8•2/7•1/6≈0,01786.
Ймовірність вибрати 1 підручник з математики означає 1 з 5 з математики, і 2 з 3 з фізики.
Ймовірність вибрати першим математику рівна 5/8, другим фізику – 3/7, третім фізику – 2/6.
Плюс ще треба врахувати перестановки з 3 по 1 (A31=3), оскільки математика може бути вибрана в ряді першою, другою або третьою, тобто набори
МФФ, ФМФ, ФФМ.
Обчислюємо p(1):
p(1)=3•5/8•3/7•2/6≈0,2678.
Ймовірність вийняти дві книжки з математики з 3:
ММФ, МФМ, ФММ.
Ймовірність вибрати матем. першою рівна 5/8, другою – 4/7, далі фізику – 3/6.
p(2)=3•5/8•4/7•3/6≈0,5357.
Ймовірність взяти 3 книги з 5 з математики серед 8 рівна
p(3)=5/8•4/7•3/6≈0,1786.
Тому що першою беремо одну з 5 книг серед 8, другою 1 з 4 серед 7, третьою – 1 з 3 математик з 8 книг.
Це надіюсь Вам легко усвідомити.
2 спосіб
Обчислимо через формули ймовірності. Оскільки нам неважливо яка з книг з математики чи фізики попаде в набір, а лише їх кількість, то застосовуємо формулу комбінацій. Кількість можливих способів вибрати 3 книги з 8 рівна
N=C83=8!/(3!•5!)=56.
Кількість способів вибрати k=0..3 книг з 5 з математики дорівнює
m1=C5k=5!/(k!•(5-k)!).
3-k книг з фізики можна вибрати m2 способами
m2=C33-k=3!/(k!•(3-k)!).
Тому за теоремою множення ймовірностей
p(k)=m1•m2/N.
При обчисленнях отримаємо ті ж значення, що і першим способом.
Записуємо результати в таблицю закону розподілу
|
X |
0 |
1 |
2 |
3 |
|
p |
0,01786 |
0,2678 |
0,5357 |
0,1786 |
Це тільки пів завдання, далі обчислюємо математичне сподівання за формулою
M(x)=sum(xi•pi,i=0..3)=1•0,2678+2•0,5357+3•0,1786=1,626.
Формула дисперсії
M(x)=sum(xi2•pi,i=0..3)-M2(X)=0,6278.
Середнє квадратичне відхилення рівне кореню з дисперсії
σ(X)=√0,6278≈0,7923.
Всі числові характеристики розподілу знайдені.
Приклад 3. Ймовірність того, що покупець, який завітав до взуттєвого магазину, здійснить покупку дорівнює в середньому 0,1. Яка ймовірність того, що із 400 покупців, що завітали до магазину покупку здійснять: а) 40 покупців; б) від 50 до 80 покупців.
Обчислення: Найточніше і найшвидше розрахунки можна провести на комп'ютері з допомогою математичних пакетів, зокрема в мейплі вся відповідь має вигляд:
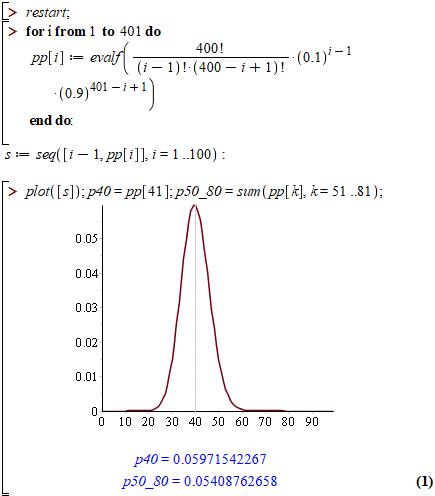
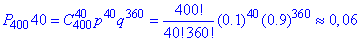
Тут Вам і закон ймовірностей, графік і шукані ймовірності в точці та на інтервалі.
На практиці колись до таких степенів ніхто не розраховував і факторіали від великих чисел не брали. Тому придумали наближені функції, якими як і 100 років тому, проведемо обчислення.
Перше значення P40040 за локальною формулою Лапласа.
Тоді ймовірність що серед 400 людей покупку зроблять 40 рівна 0,047
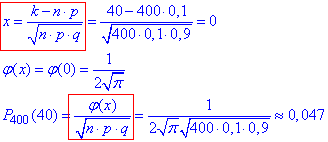
Як бачите похибка між точним значенням 0,0597 і наближеним 0,047 велика, але це вважалося нормальною збіжністю і всі наближені формули вчать по сьогодні, хоча на мою думку, такі обчислення зайві.
Далі ще інтересніше, ймовірність, що від 50 до 80 покупців за іншою – інтегральною формулою Лапласа.
Для k1=50 і k2=80 знайдемо "ікси" за формулою
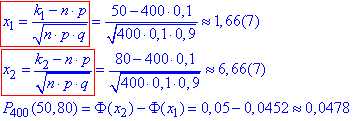
Інтегральну функцію Лапласа в точках "ікс1, ікс2" також обчислювали в мейплі.
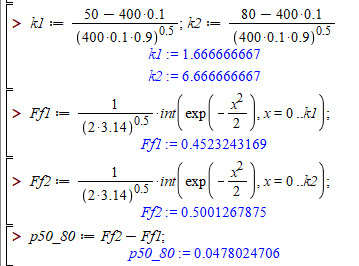
Думаю,якщо шукати онлайн таблиці інтегральної функції Лапласа, то похибка обчислень була б більшою через грубу табуляцію.
Загалом бачимо, що розходження між точним значенням 0,054 і наближеним 0,0478 досить відчутне.
Формули математичного сподівання, дисперсії та середнього квадратичного відхилення
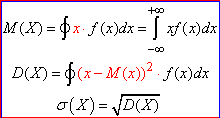
Приклад 1. Для якого значення k функція f(x)=k*exp(-(x^2+4x+4)) є щільністю розподілу випадкової величини Х?
Знайти M(X), D(X), σ(X) і обчислити
P(-4<X<-2.9).
Розв'язання: Задана щільність розподілу змінюється за експоненціальним законом, тому визначена на всій дійсній осі. Щоб вона мала властивості щільності розподілу необхідно, щоб інтеграл по всій множині значень (x∈R) був рівним одиниці (int(f(x),x)=1). Цю умову ще називають нормалізацією щільності розподілу. Вона потрібна для того, щоб ймовірність повної події не перевищувала одиницю. Невизначений інтеграл без мат. Пакету Ви навряд чи знайдете, бо він рівний функції erf(x)
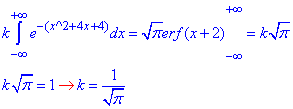
Далі, визначивши k, обчислюємо інтегруванням числові характеристики розподілу та ймовірність попадання в інтервал
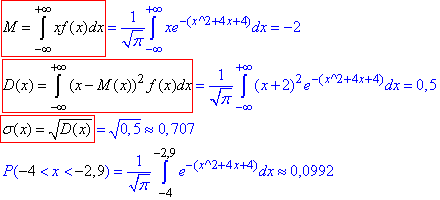
На цьому всі потрібні числові характеристики обчислено, використовуйте наведені алгоритми на практичних та екзаменах.
Приклад 2. Задано функцію розподілу F(x) неперервної випадкової величини X:
F(x)=0
F(x)=(x^3+2x)/12, x∈(0;2] ;
F(x)=1, x>2.
Знайти щільність розподілу f(x) і числові характеристики M(x), D(x), σ(x).
Розв'язання: Щільність розподілу знаходимо диференціюванням функції розподілу
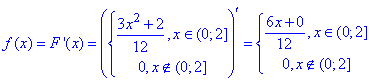
Слід пам'ятати, що функція розподілу заданана кусково неперервною функцією, тому щільність розподілу рівна нулю скрізь де щільність приймає стале значення.
Отже f(x)=0,5х, x∈(0;2] і f(x)=0 за межами інтервалу.
Щоб знайти математичне сподівання домножимо щільність розподілу на «ікс» і проінтегруємо на проміжку, де вона приймає відмінні від нуля значення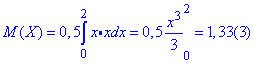
Через інтеграл знаходимо дисперсію.
Для цього інтегруємо щільність домножену на множник, який рівний (x-M(X))^2.
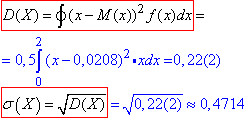
Середнє квадратичне відхилення це корінь з дисперсії.
Наведемо фрагмент коду з мат. пакету Мейпл

Приклад 3. Щільність розподілу випадкового вектора (X,Y) має вигляд f(x,y)=(3x+y)/7, x∈[0;2], y∈[0;1] і f(x,y)=0 в інших випадках.
Знайти середнє квадратичне відхилення складової Y.
Розв'язання: Для обчислення σ(X) нам потрбно знайти дисперсію D(Y), а в її формулу входить математичне сподівання M(Y).
Тому інтегруванням знаходимо одну величину за іншою, спершу матем. сподівання
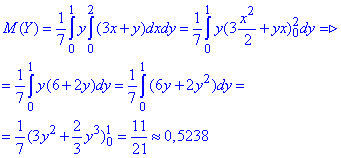
Далі обчислюємо дисперсію та середнє квадратичне відхилення
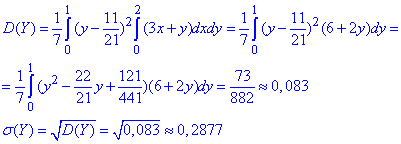
Повний інтеграл дисперсії розпишіть самостійно, ми ж взяли результат з обчислень в мейплі.
Для інтегрування служить функція int().
Математичне сподівання в мейплі можна обчислити так:
>My:=int(y*int((3*x+y),x=0..2),y=0..1);
Далі його копіюємо в другий рядок і змінюємо множник y перед внутрішнім інтегралом на (y-My)^2:
>Dy:=int((y-My)^2*int((3*x+y),x=0..2),y=0..1);
>sigma_y:=Dy^0.5;
Щоб обчислити кожен рядок проходимо командою «Enter» і отримаємо результат
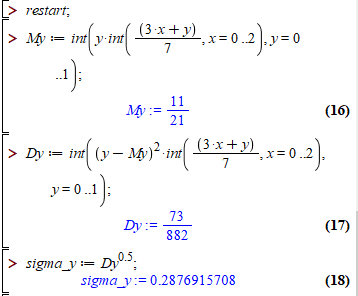
Це куди швидше, аніж по пів уроку тягнути інтеграл. Подібним чином виглядає код і в MatLab, в MathCad потрібно трохи повозитися з іконками. При теперішньому темпі розвитку ніхто на роботі не буде Вас заставляти інтегрувати вручну, максимум в мат. пакетах, або за допомогою команд в програмах, які автоматично підраховують вказані величини.
Приклад 4. Щільність розподілу ймовірностей випадкового вектора (X,Y) має вигляд f(x,y)=(2y-x)/12, якщо x∈[0;2], y∈[0,3] і рівна нулю f(x,y)=0 за межами інтервалів. Знайти математичне сподівання M(XY).
Обчислення:Математичне сподівання від добутку M(XY) обчислюємо інтегруванням щільності ймовірностей, домноженої на xy: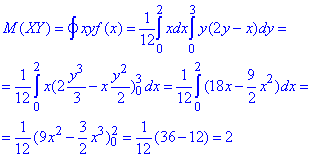
Отримали М(XY)=2.
З уроки Ви повинні запам'ятати, що інтеграл щільності розподілу по області рівний одиниці (умова нормування)+ вивчити формули числових характеристик для неперервної випадкової величини X. Все решта зводиться до інтегрування, яке Ви повинні вміти виконувати перед вивченням цієї теми.
]]>