Система двох дискретних випадкових величин (X, Y). Обчислення числових характеристик

Законом розподілу двох дискретних випадкових величин називають перелік можливих значень 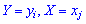та відповідних їм імовірностей спільної появи. У табличній формі цей закон має такий вигляд:При поданні таблиці використано такі позначення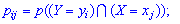

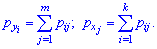
Умова нормування для двох дискретних випадкових величин має наступний вигляд:

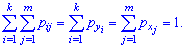
Умова нормування

Основні числові характеристики для випадкових величин X, Y, що утворюють систему (X, Y)

Математичне сподівання визначається за формулою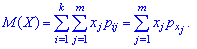

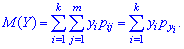
Дисперсія та середнє квадратичне відхилення для кожної дискретної величини визначають за правилами

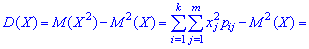
дисперсія

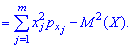
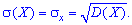
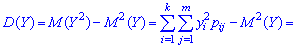
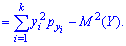
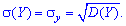Під час вивчення системи двох і більше випадкових величин доводиться з'ясовувати наявність зв'язку між цими величинами та його характер. З відповідною метою застосовують кореляційний момент: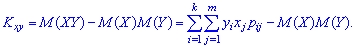У разі нульового значення кореляційного моменту K_XY=0 зв'язок між величинами X та Y, що належать системі X, Y відсутній.

Коли кореляційний момент відмінний від нуля 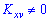, то між дискретними величинами X і Y існує кореляційний зв'язок. Тісноту кореляційного зв'язку характеризує коефіцієнт кореляції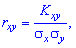який за модулнм менший одиниці 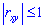, або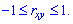
Отже, якщо випадкові величини X та Y є незалежними, то кореляційний момент рівний нулю K_XY=0 і r_XY=0. Рівність нулеві коефіцієнт кореляції r_XY є необхідною, але не достатньою умовою незалежності випадкових величин. Може існувати система залежних випадкових величин, в якої коефіцієнт кореляції дорівнює нулю. Прикладом такої системи є система двох випадкових величин , яка рівномірно розподілена всередині кола радіусом R із центром у початку координат. Дві випадкові величини X і Y називають некорельованими, якщо коефіцієнт кореляції нульовий r_XY=0, і корельованими у протилежному випадку 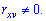Отже, якщо X і Y незалежні, то вони будуть і некорельованими. Але з некорельованості випадкових величин у загальному випадку не випливає їх незалежність.

Наведемо розв'язок поширеного на практиці прикладу.

Приклад 1. Задано закон розподілу системи двох дискретних випадкових величин (X,Y):

закон розподілу системи двох дискретних випадкових величин (X,Y)

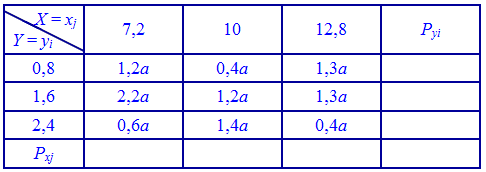
Знайти невідому константу a. Обчислити математичне сподівання, дисперсію та середнє матиматичне відхилення, кореляційний момент та коефіцієнт кореляції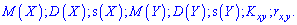

Розв'язання. Застосовуючи умову нормування, знаходимо каонстанту

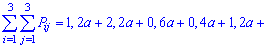
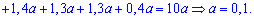
Зі знайденим a закон системи набуває такого вигляду:

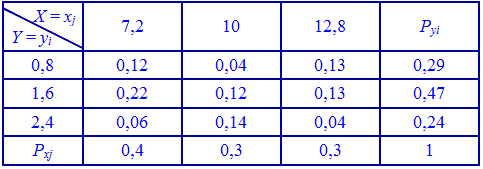
Основні числові характеристики обчислюємо за наведеними вище формулами. Математичне сподівання величини X отримає значення

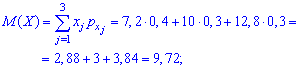
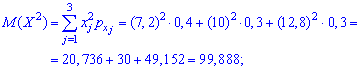
Дисперсія і середнє математичне відхилення набудуть вигляду

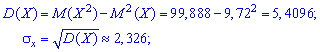
Аналогічні обчислення виконуємо для знаходження числових характеристик випадкової величини Y

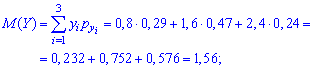
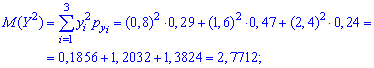
математичне сподівання

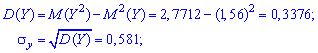
Знаходимо математичне сподівання появи обох подій
<пусто>математичне сподівання

Значення кореляційного моменту обчислюємо за формулою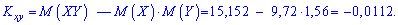 кореляційний моменту
Оскільки кореляційний момент відмінний від нуля 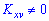, то між відповідними величинами X i Y існує кореляційний зв'язок.
Для вимірювання тісноти кореляційного зв'язку обчислимо коефіцієнт кореляції

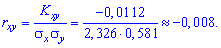
Подібних прикладів можна знайти чимало в інтернеті та розв'язниках з теорії ймовірностей. Принцип їх розв'язування залишається незмінним, тому добре проаналізуйте наведений приклад. Якщо виникають труднощі в обчисленнях - звертайтеся, ми Вам допоможемо.