Регресійний аналіз між двома випадковими величинами дозволяє встановити чи існує між ними зв'язок та міру кореляції величин.
Параметри рівняння регресії - це складові рівняння прямої регресії, якщо між випадковими величинами існує лінійний зв'язок.
Щоб підтвердити гіпотезу про лінійність зв'язку між двома випадковими величинами обчислюють вибірковий коефіцієнт кореляції.
Далі будуть дані готові відповіді до завдань з теорії ймовірностей на знаходження рівняння прямої регресії між випадковими величинами та наведені відповідні графіки. Теорію та необхідні формули можете переглянути з попередніх уроків, або виписати з наведених далі задач.
Приклад 1 За вибірковими даними в таблиці подано значення пари випадкових величин (Х, У).

Знайти вибірковий коефіцієнт кореляції пари та рівняня регресії У на Х та Х на У.
Побудувати графік випадкових величин та прямої регресії.
Обчислення: Алгоритм обчислень однаковий для всіх задач такого типу і полягає в наступних кроках.
Спершу знаходимо середні значення вибірок
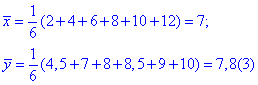
Це звичайна формула середніх, тому на ній зупинятися не будемо.
Знаходимо величини, які фігурують в формулі прямої регресії коефіцієнтами рівняння alpha, beta
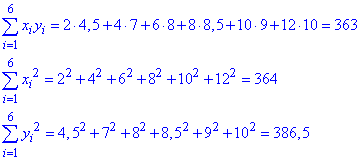
Складові рівняння alpha, beta знаходимо за формулою
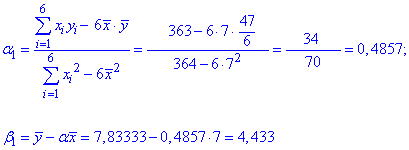
Рівняння регресії y на x це пряма наступного вигляду
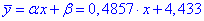
Далі знаходимо рівняння регресії x на y
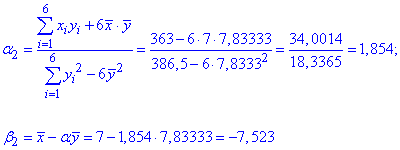
Для цього попереднє рівняння записуємо в симетричній формі відносно випадкових величин.
Є простіший спосіб: якщо маємо рівняння y(x), то з нього можемо виразити x(y), без необхідності пошуку по новому коефіцієнтів рівняння прямої.
Але викладачі, як правило, проти такої практики, хоча на практиці рівняння прямої від цього не зміниться, хіба що точність рівняння внаслідок округлень.
За знайденими коефіцієнтами складаємо рівняння регресії y на x
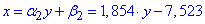
Графік прямої регресії має вигляд
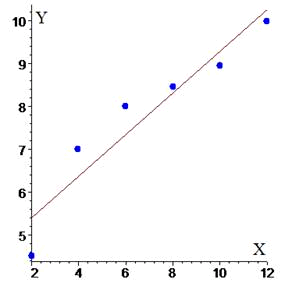
Сам графік краще будувати в будь якому з відомих вам математичних пакетів, наприклад Maple, MathCad, MatLab.
Обчислення теж вартує запрограмувати, оскільки у Вас будуть змінюватися тільки значення вибірок і кількість стовпців в таблиці (розміри масивів).
Таким чином, один раз записавши формули, можна користуватися універсальною програмою, яка в залежності від розміру виборок швидко все порахує.
Але це вже на Ваш вибір, навчальні програми у всіх різні, одних студентів вчать автоматизовувати по мірі можливості всі задачі.
Решту - важко заставити виконати просту підстановку власних даних в прості формули.
Далі буде наведена дещо інша схема знаходження рівняння регресії між двома випадковими величинами.
Алгоритм обчислень пов'язаний із знаходженням коефіцієнтів для системи двох лінійних рівнянь з двома невідомими за формулами, які фігурували вище в першому прикладі.
Приклад 2 За вибірковими даними пару випадкових величин (Х,У).

Знайти вибірковий коефіцієнт кореляції пари і рівняня регресії У на Х та Х на У.
Обчислення: Скористаємося для підрахунку коефіцієнтів лінії регресії системою рівнянь
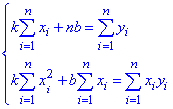
Після підстановки значень та спрощень отримаємо
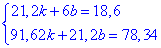
Можете виконати первірку наведених обчислень самостійно.
Звідси, знаходимо розв’язок системи 2 рівнянь
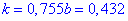
Вибіркове рівняння регресії Y на X має вигляд
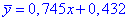
Для знаходження рівняння регресії X на Y можна скористатися знайденим рівняннм прямої, або в системі рівнянь поміняти змінні місцями
При підрахунку коефіцієнтів система двох рівнянь матиме вигляд
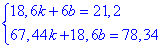
Звідси, методом вираження однієї змінної через другу та підстановкою в одне з рівнянь, знаходимо дві невідомі
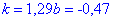
Складаємо рівняння регресії X на Y
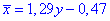
Графік рівняння регресії, побудований в пакеті Maple, має вигляд. Бачимо, що значення добре корелюють між собою.
міру кореляції можна визначити через вибірковий коефіцієнт кореляції, але про це піде мова в наступних статтях.
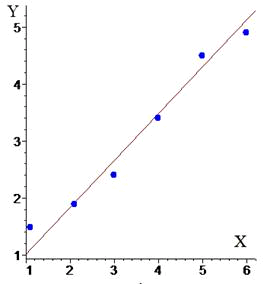
Як бачите обчислення на практиці не важкі. Побудова рівняння регресії з однієї сторони дозволяє переконатися, що всі обрахунки виконані правильно.
З іншої показує, що ми шукаємо і для чого.
Оскільки, зубрити теорію завдання невдячне і нікому не потрібне.
А от знання, де її застосувати та для чого, робить з Вас спеціаліста фаху, який обрали.


