Щільність імовірностей f(x, y) системи двох неперервних випадкових величин

Характеристикою системи неперервних випадкових величин є щільність імовірностей. Для визначення щільності ймовірностей системи двох неперервних випадкових величин (X,Y) застосовується формула

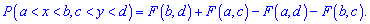
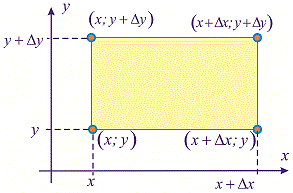
Розглянемо прямокутник зі сторонами "деьта ікс" 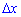та "деьта ігрик"

Імовірність розміщення системи (X,Y) у прямокутній області 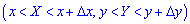обчислюється за формулою


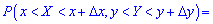
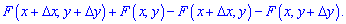
Поділивши цю ймовірність на площу прямокутника 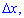і спрямувавши "деьта ікс" до нуля 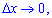дістанемо ймовірність у точці, тобто щільність:

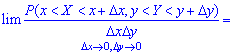
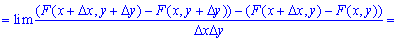
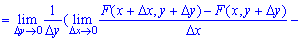
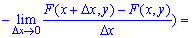
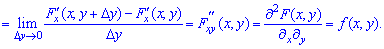
Отже, щільність розподілу ймовірностей системи двох випадкових величин визначається залежністю

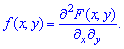
Функція щільності f(x,y) може існувати лише за умови, що F(x,y) є неперервною за аргументами x і y та двічі диференційовною. Функції f(x,y) у тривимірному просторі відповідає певна поверхня — так звана поверхня розподілу ймовірностей системи двох неперервних випадкових величин (X,Y). Тоді f(x,y)dxdy— імовірність розміщення системи двох випадкових величин у прямокутнику зі сторонамиdx, dy.

Властивості щільності розподілу ймовірностей системи двох неперервних випадкових величин f(x, y)

1. Щільності розподілу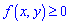 є невід'ємною функцією, оскільки F(x,y) є неспадною відносно аргументів x і y.
2. Умова нормування системи двох неперервних випадкових величин (X,Y) полягає в тому, що інтеграл по області від щільності рі:вний повній імовірності (=1)
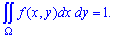Якщо область необмежена 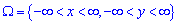, то умова нормуваннянабирає вигляду:

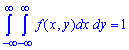
3. Імовірність розміщення системи змінних (x,y) в підмножині області 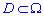обчислюється, як інтеграл по підмножині:

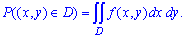
Імовірність розміщення системи змінних (x,y) у прямокутній області D=(a<x<b; c<y<d) визначається інтегруванням
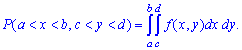4. Функція розподілу ймовірностей системи двох змінних визначається з рівняння
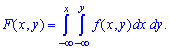5. Якщо область задана прямокутником 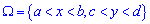, то функція розподілу ймовірностей має вигляд інтегралу

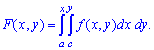
Розглянемо наступний приклад для закріплення матеріалу.

Приклад. Задано поверхню розподілу ймовірностей системи двох неперервних випадкових величин наступним законом:

функція є константою f(x,y)=a , (a=const) , якщо аргументи належать прямокутній області ;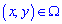
та рівна нулю f(x,y)=0 поза його межами ;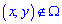
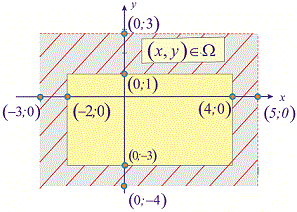
Прямокутник задано областю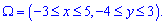
Знайти параметр a і функція розподілу ймовірностей F(x,y) . Обчислити ймовірність попадання аргументів у внутрішній прямокутник, що обмежений областю

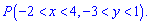
Розв'язання. Перш за все намалюємо прямокутники, які задані умовами задачі. Це внесе деяку ясність в процес розв'язування
Параметр a визначаємо з умови нормування :


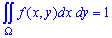
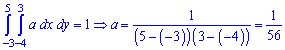
Таким чином, отримали що поверхня розподілу ймовірностей системи двох неперервних випадкових величин рівна f(x,y)=1.56 для аргументів з прямокутної області 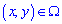і нулю f(x,y)=0 поза нею 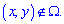Згідно 5 властивості в прямокутнику -3<x<5; -4<y<3 визначаємо закон розподілу ймовірностей

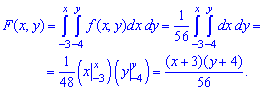
За його межами функція набуває значень Аргументи належать області y>3; -3<x<5

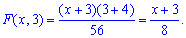
Якщо x>5; -4<y<3, то маємо

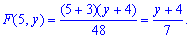
Для x>5; y>3 функція рівна одиниці

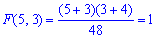
і при x<-3; y<-4 приймає нульове значення F(-3,-4)=0.
На основі вище наведених розрахунків функція розподілу ймовірностей має вигляд
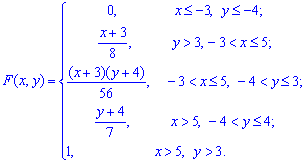Обчислюємо ймовірність попадання аргументів у внутрішній прямокутник
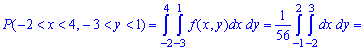
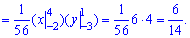Розглянемо задачу навпаки, коли задано функцію розподілу F(x,y), а потрібно знайти щільність розподілу f(x,y).

ПРАКТИКУМ з теорії ймовірностей і математичної статистики

Завдання 1.1 Функція розподілу системи випадкових величин (X;Y) має вигляд F(x,y)={0, x<0 або y<0; 1-a^-x-a^-y+a^-x-y, x≥0, y≥0}

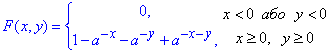
якщо a=2.
Знайти щільність розподілу f(x,y) системи (X;Y).
Розв'язування: Для визначення щільності розподілу f(x,y) системи (X;Y) для диференційовної функції F(x,y) знайдемо частинні похідні:
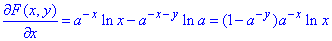- частинна похідна І порядку F(x,y) по x;
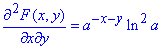- змішана частинна похідна ІІ порядку.
Підставляємо в формулу щільності розподілу

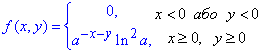
При a=2 отримаємо

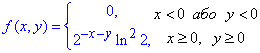
Це і є шукана щільність розподілу f(x,y) системи (X;Y). 

 Повне відшукання функції розподілу ймовірностей є досить популярним завданням на практиці і Ви повинні вміти його виконувати. Для цього потрібно інтегрувати функцію щільності ймовірностей. Таким чином вивчаючи теорію ймовірності - Ви на практиці удосконалюєте навички інтегрування.

Вас може зацікавити:
• Функція розподілу ймовірностей системи двох випадкових величин. Імовірність попадання в прямокутник
• Система двох дискретних випадкових величин (X, Y). Обчислення числових характеристик
• Як знайти щільність розподілу випадкової величини?
• Густина (щільність) розподілу імовірностей. Обчислення та побудова