Відповіді до індивідуальних завдань з теорії ймовірностей послужать для студентів математичних дисциплін доброю інструкцією на екзаменах чи тестах. Це в більшій мірі стосується студентів економічного факультету та статистів. Наведені розв'язки точно використають в навчанні економісти ЛНУ ім. І.Франка, оскільки саме там задавали все що наведено нижче. ВУЗи Києва, Одеси, Харкова та інших міст України мають подібну систему навчання, тому багато корисного для себе повинен узяти кожен студент. Завдання різної тематики поєднані між собою посиланнями у кінці статті, тож маєте можливість знайти те, що Вам потрібно.
Обчислення середнього квадратичного відхилення, медіани, моди, асиметрії
Завдання 1. Побудувати статистичний розподіл вибірки, записати емпіричну функцію розподілу та обчислити такі числові характеристики:
- вибіркове середнє;
- вибіркову дисперсію;
- підправлену дисперсію;
- вибіркове середнє квадратичне відхилення;
- підправлене середнє квадратичне відхилення;
- розмах вибірки;
- медіану;
- моду;
- квантильне відхилення;
- коефіцієнт варіації;
- коефіцієнт асиметрії ;
- ексцес для вибірки:
Вибірка задана рядом 11, 9, 8, 7, 8, 11, 10, 9, 12, 7, 6, 11, 8, 7, 10, 9, 11, 8, 13, 8.
Розв'язання:
Запишемо вибірку у вигляді варіаційного ряду (у порядку зростання):
6; 7; 7; 7; 8; 8; 8; 8; 8; 9; 9; 9; 10; 10; 11; 11; 11; 11; 12; 13.
Далі записуємо статистичний розподіл вибірки у вигляді дискретного статистичного розподілу частот:
Емпіричну функцію розподілу визначатимемо за формулою
де nx – кількість елементів вибірки, що менші за х. Використовуючи таблицю і враховуючи, що обсяг вибірки рівний n=20, запишемо емпіричну функцію розподілу:
Далі обчислимо числові характеристики статистичного розподілу вибірки.
Вибіркове середнє обчислюємо за формулою
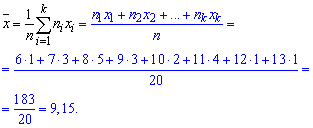
Вибіркову дисперсію знаходимо за формулою
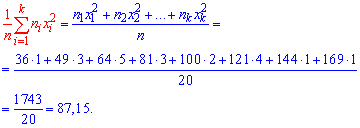
Вибіркове середнє, що фігурує в формулі у квадраті знайдено вище. Залишається все підставити у формулу
Підправлену дисперсію обчислюємо за формулою
Вибіркове середнє квадратичне відхилення обчислюємо за формулою
Підправлене середнє квадратичне відхилення обчислюємо за формулою
Розмах вибірки обчислюємо як різницю між найбільшим і найменшим значеннями її варіант, тобто:
Медіану обчислюють за формулами:
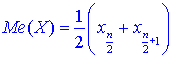якщо число n – парне;
якщо число п – непарне.
Тут беремо індекси в xi згідно з нумерацією варіант у варіаційному ряді.
У нашому випадку п=20, тому
Мода – це варіанта, яка у варіаційному ряді трапляється найчастіше, тобто
Квантильне відхилення знаходять за формулою
де 
– перший квантиль, 
– третій квантиль.
Квантилі отримуємо при розбитті варіаційного ряду на 4 однакові частини.
Для заданого статистичного розподілу квантильне відхилення прийме значення
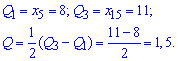
Коефіцієнт варіації рівний процентному відношенню підправленого середнього квадратичного до вибіркового середнього
Коефіцієнт асиметрії обчислюємо за формулою
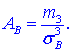
Тут m3 - центральний емпіричний момент 3-го порядку,
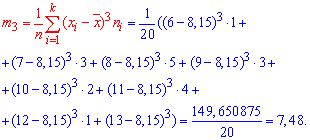
Підставляємо у формулу коефіцієнта асиметрії
Ексцесом 
статистичного розподілу вибірки називається число, яке обчислюється за формулою:
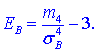
Тут m4 - центральний емпіричний момент 4-го порядку. Знаходимо момент
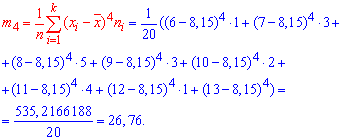
а далі ексцес
Тепер Ви маєте усі потрібні формули і знаєте, як знайти числові характеристики статистичного розподілу. Решта розв'язків індивідуальних завдань Ви знайдете в наступних матеріалах.
