Цілочислова випадкова величина X має біноміальний закон розподілу, якщо ймовірність її можливих значень обчислюється за формулою Бернуллі:
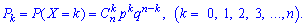
У табличній формі цей закон набирає такого вигляду:
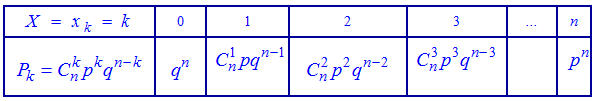
При перевірці виконання умови нормування використовується формула біному Ньютона, тому закон розподілу називають біноміальним
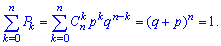Побудуємо ймовірнісну твірну функцію для цього закону
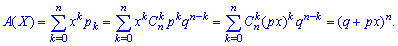Отже, імовірнісна твірна функція для біноміального закону
Знайдемо основні числові характеристики для цього закону:
1. Математичне сподівання випадкової величини через твірну функцію для біноміального розподілу матиме запис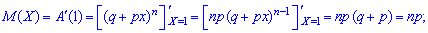
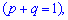
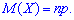
2. Друга похідна від твірної функції для біноміального розподілу в одиниці прийме значення
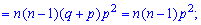
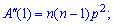
На основі знайденого значення можна обчислювати дисперсію за формулою
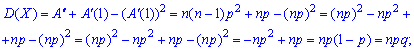
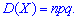Маючи дисперсію не важко встановити середнє квадратичне відхилення
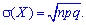
3. Коефіцієнт асиметрії А(Х) та ексцес Е(Х) для біноміального розподілу визначають за формулами
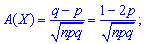
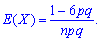
У випадку зростання кількості випробувань n асиметрія та ексцес прямують до нуля.
Розв'язи завдань на біноміальний розподіл
Задача 1. У партії однотипних деталей стандартні становлять 97%. Навмання з партії беруть 400 деталей. Визначити математичне сподівання, дисперсію та середнє квадратичне відхилення М(Х), D(X), S(Х) для дискретної випадкової величини Х — появи числа стандартних деталей серед 400 навмання взятих.
Розв'язання. Цілочислова випадкова величина Х має біноміальний закон розподілу ймовірностей, яка може набувати значення Х = k = 0, 1, 2, ..., 400. Імовірності можливих значень для даного завдання визначаються за формулою Бернуллі і становлять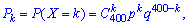 
де р = 0,97 — імовірність появи стандартної деталі, q = 1 – p =1 – 0,97 = 0,03 — імовірність появи нестандартної деталі. Згідно з наведеними вище формулами визначаємо
математичне подівання
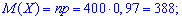
диперсію
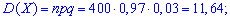
середнє квадратичне відхилення
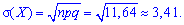
Розрахунки дя біноміального закону достатньо прості.
Задача 2. Два ювелірні заводи виробляють весільні кільця в об'ємі 3:7. Перший завод виготовляє 95% обручок без дефекту, другий – 90%. Молода пара перед весіллям купляє пару обручок. Побудувати закон розподілу, обчислити математичне сподівання та середнє квадратичне відхиленння.
Розв'язання. Імовірність події А – куплена обручка виявилася якісною визначимо за формулою повної імовірності
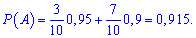
Випадкова величина Х – кількість кілець належної якості серед куплених має біноміальний закон розподілу з параметрами
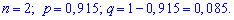
Знайдемо відповідні ймовірності
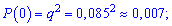
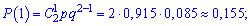
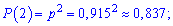
Та запишемо таблицю розподілу
На основі табличних даних обчислюємо математичне сподівання
дисперсію
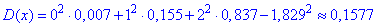
Середнє квадратичне відхилення через корінь з дисперсії прийме значення
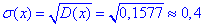
Як можна переконатися з прикладів, біноміальльний закон розподілу простий як для розуміння так ідля обчислень. Добре розберіться з прикладами та користуйтеся біноміальним розподілом там де це необхідно.
