Для знаходження моди та медіани випадкової величини потрібні добрі вміння інтегрувати та знання наступного теоретичного матеріалу. Модою M0 дискретної випадкової величини X називають те її можливе значення, якому відповідає найбільша ймовірність появи (тобто таке значення величини X, яке трапляється найчастіше при проведенні експериментів, дослідів, спостережень). У випадку неперервної випадкової величини модою називають те її можливе значення, якому відповідає максимальне значення щільності ймовірностей
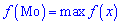
В залежності від вигляду функцію f(x) випадкова величина X може мати різну кількість мод. Якщо випадкова величина має одну моду, то такий розподіл імовірностей називають одномодальним; якщо розподіл має дві моди — двомодальним і більше – мультимодальним.
Існують і такі розподіли, які не мають моди, їх називають антимодальними. Медіаною Meнеперервної випадкової величини X називають те її значення, для якого виконуються рівність імовірностей подій, тобто щільність імовірностей справа та зліва однакові та рівні половині (0,5)
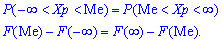
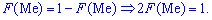
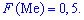Графічно мода і медіана зображені на рисунку
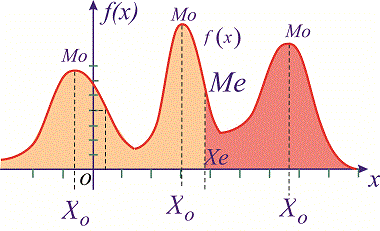
При такому значенню випадкової величини графік функції розподілу ділиться на частини з однаковою площею. Неперервна випадкова величина має лише одне значення медіани. Для дискретної випадкової величини медіану зазвичай не визначають, проте в деякій літературі наводяться правила, згідно яких, для ряду випадкових величин розміщених в порядку зростання (варіаційного ряду) моду визначають згідно розподілу: якщо маємо непарну кількість випадкових величин N=2k+1 то медіана рівна середній величині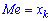
у випадку парної кількості N=2k півсумі середніх величин
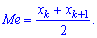Розглянемо приклади визначення моди та медіани.
Приклад 1. В розважальному центрі працівник обслуговує чотири доріжки для боулінгу. Імовірність того, що котрась доріжка потребує прибирання протягом зміни є сталою величиною з ймовірністю 85%.
Побудувати закон розподілу ймовірностей дискретної випадкової величини X — кількість доріжок, які потребують прибирання. Знайти моду X.
Розв'язання. Випадкова величина може приймати значення
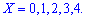
Імовірності появи значень визначаємо за твірною функцією
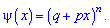
Для заданої задачі вхідні величини приймають значення
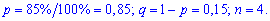
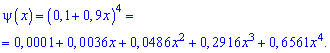
Шукані ймовірності входять множниками при степенях аргумента
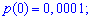
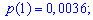
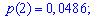
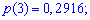
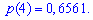
Закон розподілу ймовірностей запишемо у вигляді таблиці
Із таблиці визначаємо моду Mo=4, як значення при максимальній ймовірності. Отримали одномодальний розподіл.
Приклад 2. За заданою щільністю ймовірностей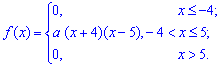
Знайти параметр a , щільність ймовірностей F(x), моду Mo.
Розв'язання. Застосовуючи умову нормування виконуємо інтегрування щільності розподілу
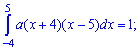
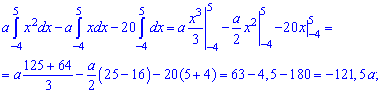
після того визначаємо параметр
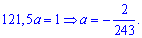
Щільність імовірностей, враховуючи знайдене значення матиме вигляд
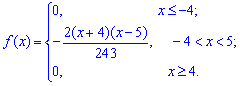
а її графік зображено на рисунку нижче
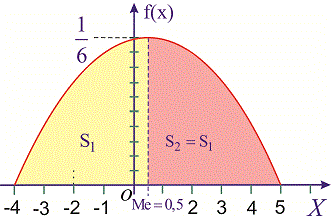
З графіка щільності ймовірностей бачимо, що мода приймає значення Mo=0,5. Визначимо медіану Me за допомогою функції розподілу ймовірностей. ЇЇ значення на проміжку [-4; 5] знаходимо інтегруванням
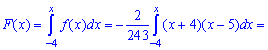
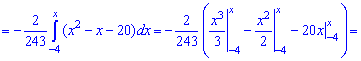
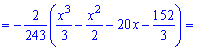
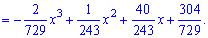
Функція розподілу матиме наступний вигляд
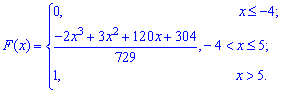
а її графік матиме вигляд
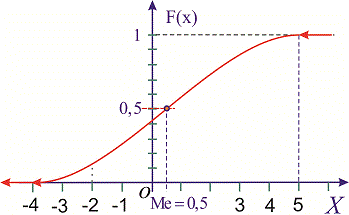
Для визначення медіани випадкової величини Me застосовуємо формулу
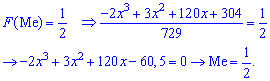
Медіану Me можна знайти за допомогою щільності ймовірностей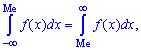 
для дискретної випадкової величини з проміжку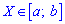 
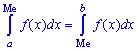Таким чином медіану Me — можливе значення випадкової величини X, при якому пряма, що проведена перпендикулярно до відповідної точки на площині X=Me, ділить площу фігури, яка обмежена функцією щільності ймовірностей f(x) на дві рівні частини.
Завдання на визначення моди та медіани випадкової величини зустрічаються на практиці не так часто, як щільності розподілу ймовірностей, однак наведений вище теоретичний матеріал та розв'язки поширених прикладів допоможуть Вам знаходити ці велечини без великих затрат часу. При необхідності Ви завжди можете замовити розв'язання задач з теорії ймовірностей у нас.
ul>Вас може зацікавити:
