Математичне сподівання не дає достатньо повної інформації про випадкову величину, оскільки одному й тому самому значенню математичного сподівання M(X) може відповідати безліч випадкових величин, які будуть різнитися не лише можливими значеннями, а й характером розподілу і самою природою можливих значень.
Наприклад. Закони розподілу двох випадкових величин X і Y задані таблицями:
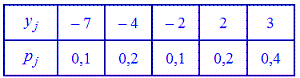
Обчислити математичне сподівання M(X) і M(Y)
Розв'язання. Знаходимо математичне сподівання за формулами
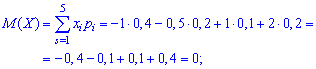
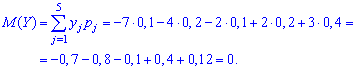
Отримали, що для двох різних законів розподілу математичні сподівання приймають однакові значення (0), при цьому можливі значення для випадкових величин X і Y різняться. Із наведеного прикладу бачимо, що в разі рівності математичних сподівань (M(X)=M(Y)=0) випадкові величини X і Y мають тенденцію до коливань відносно M(X) та M(Y) причому Y має більший розмах розсіювання відносно M(Y) порівняно з випадковою величиною X відносно M(X). Тому математичне сподівання ще називають центром розсіювання. Для визначення розсіювання вводиться числова характеристика, яку називають дисперсією.
Для визначення дисперсії розглядається відхилення випадкової величини X від свого математичного сподівання
(X-M(X))
Математичне сподівання такого відхилення випадкової величини X завжди дорівнює нулю. В цьому легко переконатися із наступного співвідношення
M(X-M(X))=M(X)-M(M(X))=M(X)-M(X)=0
Таки чином, відхилення не може бути мірою розсіювання випадкової величини.
Дисперсією випадкової величини X називають математичне сподівання квадрата відхилення випадкової величини X від свого математичного сподівання (X-M(X))
D(X)=M(X-M(X))2
Для дискретної випадкової величини X дисперсія обчислюється за формулою
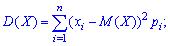
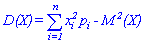
для неперервної знаходять інтегруванням
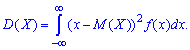
Якщо неперервна величина задана на інтервалі X∈[a,b] то дисперсія рівна інтегралу зі сталими межами інтегрування
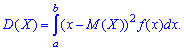
Властивості дисперсії
1. Якщо випадкова величина складається з однієї тотчки С=const — стала величина, то дисперсія рівна нулю D(C)=0.
2. Дисперсія від добутку сталої на випадкову величину рівна квадрату сталої помноженому на дисперсію випадкової величини
D(C*X)=C2D(X)
3. Якщо A і B — сталі величини, то для дисперсії D(A*X+B) справедлива залежність
D(A*X+B)=A2D(X)
Це випливає з двох попередніх властивостей.
Дисперсію можна обчислити за спрощеною формулою:
D(X)=M(X2)-M2(X)
яка у випадку дискретної випадкової величини X має вигляд
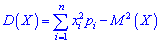
для неперервної визначається залежністю
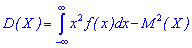
і для неперервної на проміжку X∈[a,b] співвідношенням
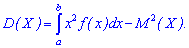
Наведені формули дуже зручні в обчисленнях, і їх, на відміну від попередніх, використовують в навчанні
Також слід пам'ятати, що дисперсія завжди приймає невід'ємні значення D(X≥0). Вона характеризує розсіювання випадкової величини відносно свого математичного сподівання. Якщо випадкова величина виміряна в деяких одиницях, то дисперсія вимірюватиметься в цих самих одиницях, але в квадраті.
Для порівняння зручно зручно користуватися числовими характеристиками однакової розмірності з випадковою величиною. Для цього вводять в розгляд середнє квадратичне відхилення – корінь квадратний із дисперсії. Її позначають грецькою літерою «сігма»
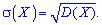
Розглянемо приклади для ознайомлення з практичною стороною визначення цих величин.
Приклади обчислення дисперсії та середнього квадратичного відхилення
Приклад 1. Закон розподілу дискретної випадкової величини X задано таблицею:
Обчислити дисперсію D(X) та середнє квадратичне відхилення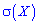 
.
Розв'язання. Згідно з властивостями дисперсії знаходимо
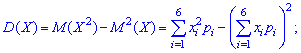
Математичне сподівання обчислюємо за формулою
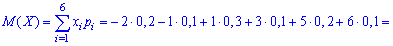
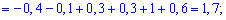
Далі знаходимо M(X2)
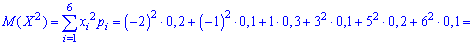
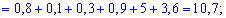
та дисперсію
D(X)=10,7-(1,7)2=10,7-2,89=7,81
Середнє квадратичне відхилення рівне ореню з дисперсії
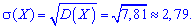
На цьому обчислення завершені і Ви можете переконатися, що знаходження імовірнісних характеристик на практиці доволі просто реалізувати. Кому важко все це рахувати вручну, можна написати програмку в Exel, Pascal. З однієї сторони не важко, з другої - один раз зробии і постійно користуєтеся.
Приклад 2. Маємо чотири електричні лампочки, кожна з яких має дефект з імовірністю q=0,2 (p=1-q=0,8 — імовірність того, що лампочка без дефекту). Послідовно беруть по одній лампочці, вкручують у патрон і вмикають електричний струм. Під час вмикання струму лампочка може перегоріти, і її заміняють на іншу. Побудувати закон розподілу дискретної випадкової величини X — число лампочок, які будуть випробувані. Обчислити середнє квадратичне відхилення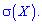 
Розв'язання. Дискретна випадкова величина X — число лампочок, які будуть випробувані — набуває таких можливих значень:
x1=1, x2=2, x3=3, x4=4.
Обчислимо відповідні ймовірності:
P(X=1)=p1=0,8;
P(X=2)=p2=pq=0,16;
P(X=3)=p3=pq2=0,032;
P(X=4)=p4=pq3+q4=0,0064+0,0016=0,008.
Останню ймовірність можна трактувати наступним чином: четверта лампочка буде випробувана, коли третя перегорить, а четверта — ні, або коли й четверта перегорить.
У табличній формі закон розподілу X матиме наступний вигляд:
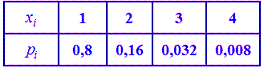
Для знаходження середнього квадратичного відхилення знайдемо спочатку значення дисперсії. Для дискретної випадкової величини знаходимо спершу математичні сподівання:
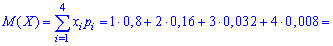
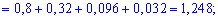
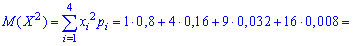
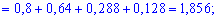
Знаходимо дисперсію випадкової величини
D(X)=M(X2)-M2(X)=1,856-(1,248)2=0,298296.
Середнє квадратичне відхилення знаходимо добуванням кореня квадратного із дисперсії.
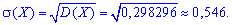
Завдання завершено встановленням усіх потрібних характеристик. Основна хитрість тут у тому, що для середнього квадратичного відхилення хоч не хоч, а потрібно шукати всі попередні величини.
Приклад 3. Закон розподілу ймовірностей дискретної випадкової величини X задано у вигляді функції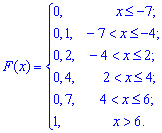
Обчислити середнє квадратичне відхилення D(X) і дисперсію σ(X).
Розв'язання. За допомогою функції розподілу ймовірностей формуємо закон розподілу у вигляді таблиці
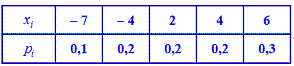
На основі таблиці розподілу обчислюємо просту медіану, медіану квадрату величини.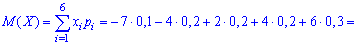
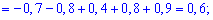
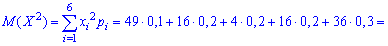
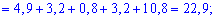
Далі знаходимо дисперсію
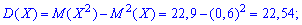
та середнє квадратичне відхилення
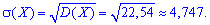
Подібних прикладів можна навести велику кількість, основна їх суть в правильному застосуванні наведених на початку статті формул для обчислення дисперсії та математичного сподівання. Застосовуйте їх там де це необхідно і не допускайте помилок при визначенні дисперсії.
