Відповіді на індивідуальні завдання з теорії ймовірностей на визначення числових характеристик статистичного розподілу вибірки, знаходження рівняння регресії між двома ознаками, приклади на перевірку гіпотези А за наявної гіпотези В допоможуть успішно скласти сесію студентам. Все що Вам потрібно, це уважно розібратися з методикою знаходження усіх можливих характеристик розподілів.
Знаходження числових характеристик статистичного розподілу
Варіант 13 . Індивідуальне завдання 1.
Завдання 1. Побудувати статистичний розподіл вибірки, записати емпіричну функцію розподілу та обчислити такі числові характеристики:
- вибіркове середнє;
- вибіркову дисперсію;
- підправлену дисперсію;
- вибіркове середнє квадратичне відхилення;
- підправлене середнє квадратичне відхилення;
- розмах вибірки;
- медіану;
- моду;
- квантильне відхилення;
- коефіцієнт варіації;
- коефіцієнт асиметрії ;
- ексцес для вибірки:
Завдання сформовані у вигляді таблиці (далі – по варіантах, № варіанту = № студента у списку групи)
7, 6, 5, 8, 6, 5, 6, 9, 8, 7, 10, 5, 4, 9, 7, 9, 6, 9, 11, 6.
Розв'язання:
Запишемо вибірку у вигляді варіаційного ряду (у порядку зростання):
4; 5; 5; 5; 6; 6; 6; 6; 6; 7; 7; 7; 8; 8; 9; 9; 9; 9; 10; 11.
Запишемо статистичний розподіл вибірки у вигляді дискретного статистичного розподілу частот:
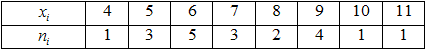Емпіричну функцію розподілу визначатимемо за формулою
де nx кількість елементів вибірки, що менші за х.
Використовуючи таблицю і враховуючи, що обсяг вибірки
запишемо емпіричну функцію розподілу:
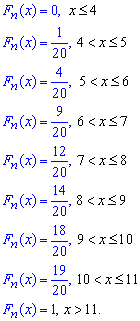
Далі обчислимо числові характеристики статистичного розподілу вибірки.
1) Вибіркове середнє знайдемо за формулою
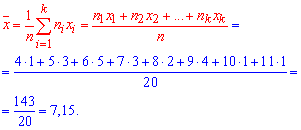
2) Вибіркову дисперсію обчислюємо за формулою
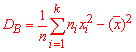
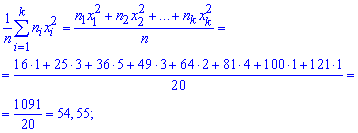
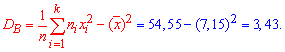
3) Підправлену дисперсію знаходимо за формулою
4) Вибіркове середнє квадратичне відхилення обчислюємо за формулою
5) Підправлене середнє квадратичне відхилення знаходимо з формули
6) Розмах вибірки визначаємо як різницю між найбільшим і найменшим значеннями її варіантів, тобто:
7) Медіану обчислюють за формулами:
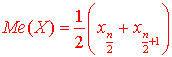
якщо число n – парне;
якщо число п – непарне.
Тут беремо індекси в 
згідно з нумерацією варіант у варіаційному ряді.
У нашому випадку п=20, тому
8) Мода – це варіанта, яка у варіаційному ряді трапляється найчастіше, тобто Mo(X)=6.
9) Квантильне відхилення обчислюють за формулою
де 
– перший квантиль, 
– третій квантиль.
Квантилі отримуємо, якщо варіаційний ряд розбити на 4 однакові частини.
У нашому випадку
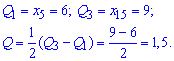
10) Коефіцієнт варіації встановимо із залежності
11) Обчислюємо коефіцієнт асиметрії
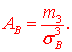
Тут 
центральний емпіричний момент 3-го порядку,
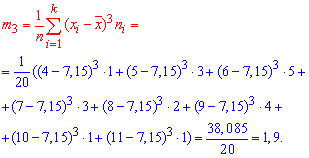
Отже, коефіцієнт асиметрії рівний 0,3
12) Ексцесом EB статистичного розподілу вибірки називається число, яке знаходять за формулою:
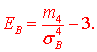
Тут m4 центральний емпіричний момент 4-го порядку,
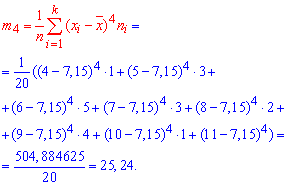
Отже, отримаємо від'ємний ексцес
На цьому індивідуальне завдання №1 розв'язано. З нього Ви повинні навчитися знаходити числові характеристики дискретного розподілу.
