На попередньому уроці розібрано перші 3 завдання на біноміальний, гіпергеометричний та рівномірний закони розподілу. Далі наведемо ще три задачі з поясненнями та графіками закону та функції розподілу.
Приклад 4 У ящику лежать 6 виробів, з яких один виріб бракований. З ящика виймають вироби один за одним до тих пір, поки не буде вийнято бракований виріб.
Потрібно знайти:
- а) закон розподілу дискретної випадкової величини X, рівній числу вийнятих виробів;
- б) функцію розподілу випадкової величини X та побудувати її графік;
- в) математичне сподівання випадкової величини X;
- г) дисперсію і середнє квадратичне відхилення випадкової величини X;
- д) ймовірності попадання в інтервали Xє[4;5], X>5, X<4.
Розв'язання: а) Нехай X - випадкова величина, що визначає число спроб при вийняті виробів.
Оскільки у ящику 6 виробів, то X може набувати значень від 1 до 6.
Якщо перший взятий виріб буде бракований, то X=1 і P1(X)=1/6.
Якщо перший взятий виріб буде нормальним, то беремо наступний (таких виробів є 5 з 6). Якщо другий виріб буде бракованим, то число спроб буде 2, тоді
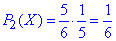
і так далі
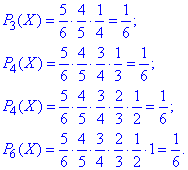
Випадкова величина X має рівномірний дискретний розподіл.
Результати запишемо в таблицю:

Графік закону розподілу має вигляд прямої
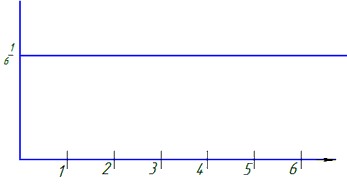
б) Функцію розподілу випадкової величини X знайдемо за формулою суми
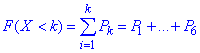
Результати запишемо в таблицю:
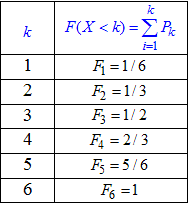
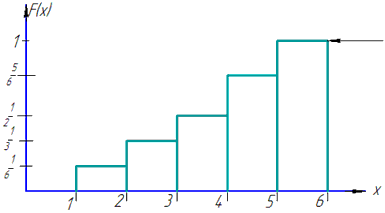
Графік функції розподілу має вигляд
в) Математичне сподівання випадкової величини =3,5
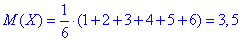
г) Дисперсія рівна 1,917
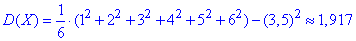
Середнє квадратичне відхилення випадкової величини X рівне 1,38:
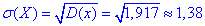
д) Ймовірності попадання в інтервали випадкової величини X
Xє[4;5] (4 або 5 разів):
p=P4+P5=1/3;
X>5 (тобто можливо лише 6 разів):
p=P6=1/6;
X<4 (від 0 до 3 разів 3*1/6):
p=P1+P2+P3=0,5
Приклад 5 Монету підкидають 11 разів.
Потрібно знайти характеристики закону розподілу, побудувати усі графіки (умови ті ж самі що і в завдання 4):
- д) ймовірності попадання в інтервали Xє[4;9], X>b, X<a.
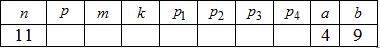
Розв'язання: а) Оскільки від досліду до досліду ймовірність залишається сталою (а саме p=q=0.5) то ймовірність випадань герба змінюється за біноміальним законом : 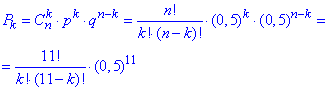
Запам'ятайте, що біноміальний розподіл найбільш поширений на практиці, на нього найбільше готових завдань.
Результати подані в таблиці:
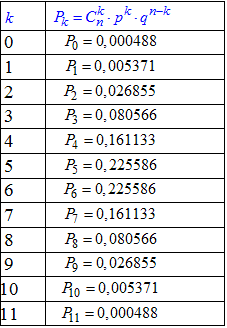
Графік закону розподілу має вигляд
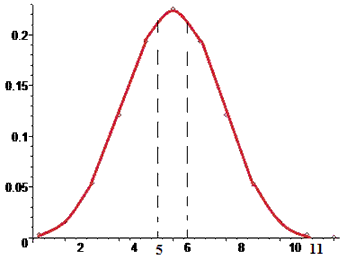
б) Функцію розподілу випадкової величини X знайдемо через формулу суми
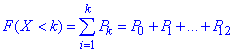
Після підрахунку отримаємо:
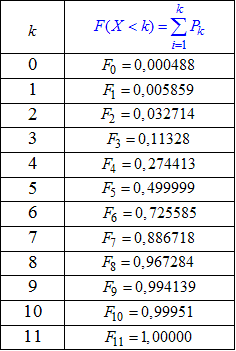
Графік функції розподілу наступний
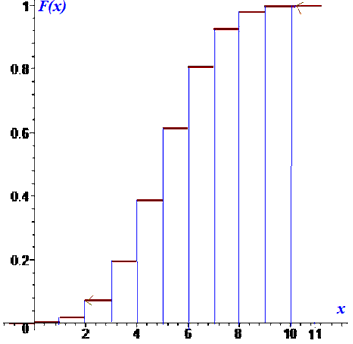
в) Знаходимо математичне сподівання випадкової величини
M(X)=n•p=11•0.5=5,5
г) Далі обчислюємо дисперсію
D(X)=n•p•q=11•0.5•0.5=2,75.
Визначаємо середнє квадратичне відхилення випадкової величини X:
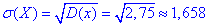
д) Ймовірності попадання в інтервали випадкової величини X наступні
Xє[4;9] (від 4 до 9 разів включно):
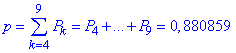
X>9 (10 або 11 разів):
p=P10+P11=0,005859
X<4 (від 0 до 3 разів - сума перших трьох значень закону розподілу):
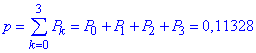
Приклад 6 В урні n=12 кульок, з яких m=3 білих, а решта чорні. З цієї урни навмання виймають k=7 кульок.
Потрібно знайти закон розподілу та побудувати його графік.
- д) ймовірності попадання в інтервали Xє[3;6], X>b, X<a.
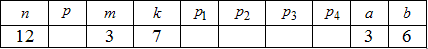
Розв'язання: а) Ймовірність Pk того, що навмання виймають l чорну кульку з 9 обчислимо за формулою (що розписана у другій задачі):
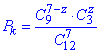
де z – кількість витягнутих білих кульок (їх не може бути більше 3),
тоді l=7-z – кількість витягнутих чорних кульок.
Випадкова величина має гіпергеометричний закон розподілу
Результати запишемо в таблицю:
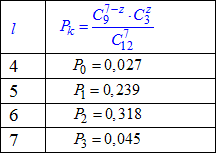
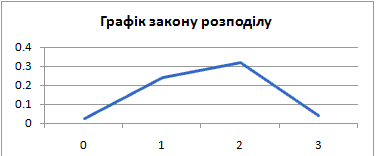
б) Функцію розподілу випадкової величини X знайдемо за формулою
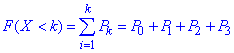
Обчислення заносимо в таблицю:
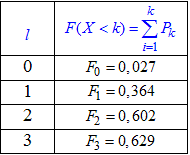
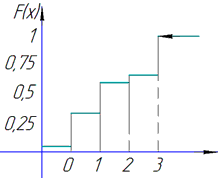
Будуємо графік функції розподілу
в) Обчислюємо математичне сподівання випадкової величини
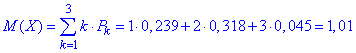
г) Знаходимо дисперсію за формулою
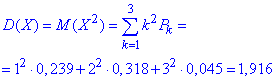
Середнє квадратичне відхилення випадкової величини X:
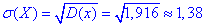
д) Ймовірності попадання в інтервали випадкової величини X
Xє[3;6] (від 3 до 6 разів включно):
p=F3=0.629;
X>6 (7 разів):
p=P0=0.027;
X<3 (0 або 1, або 2 рази), виконуємо сумування імовірностей:
p=F2=0.602
Більше готових завдань з теорії ймовірностей шукайте в даній категорії та серед відповідей до контрольних робіт.
Пам'ятайте, що наповнення сайту новими матеріалами залежить в значній мірі від Вас.
Тож діліться посиланням на корисні матеріали, надсилайте нам на пошту конспекти з практичних та замовляйте завдання!


