Сьогодні розберемо завдання на знаходження щільності розподілу неперервної випадкової величини. Можливо Ви зустрічали в літературі термін густина ймовірності - це одна і та ж сама величина.
Наведені далі приклади характерні на модулях, індивідуальних чи заліках з курсу теорії ймовірностей.
Щоб швидко відшукати правильну відповідь Ви повинні добре брати визначені інтеграли.
Для більш зацікавлених в предметі студентів наводимо код в мейплі як будувати графік щільності розподілу та виконувати інтегрування.
Аналізуйте готові відповіді та застосовуйте схему обчислень на практичних!
Приклад 1 На основі наведеної функції розподілу ймовірностей прибутку підприємця
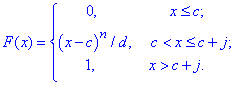
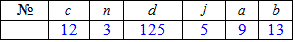
потрібно визначити:
а) щільність розподілу прибутку підприємця і нарисувати графіки функції розподілу та щільності розподілу;
б) математичне сподівання, дисперсію і середнє квадратичне відхилення прибутку підприємця;
в) ймовірність, що прибуток підприємця набуде значення з інтервалу (a;b).
Розв'язання: а) Функція розподілу є неперервною випадковою величиною, що змінюється за законом:
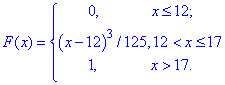
Щоб бачити як вона виглядає будемо вчитися виконувати побудову в Мейплі за допомогою функції plot().
Оскільки функція розподілу кусково неперервна то задаємо її значення на 3 інтервалах і тоді виконуємо вивід графіка функцією display(). Щоб все це працювало необхідно на початку програми підключити бібліотеку with(plots);.
В результаті отримаємо наступний розподіл:
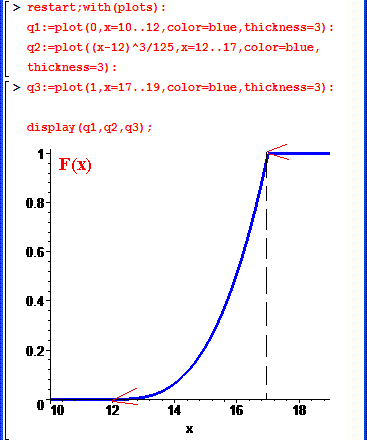
Тут ще доповнили графік підписами в paint.
Ви ж можете візуалізувати розподіл ймовірностей в MathCad, Matlab чи другому математичному пакеті.
Суть полягає в тому, що матеріал краще засвоюється, якщо його можна відчути: побачити, зміряти і т.д.
Крім того в Мейплі легко брати як визначений так і неозначений інтеграли, що корисно для наступних формул.
Щільність розподілу прибутку підприємця знаходимо через похідну розподілу
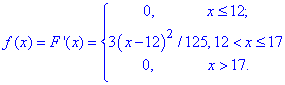
Графік щільності розподілу виконуємо дещо змінивши наведений вище код мейпла та перекомпілювавши його
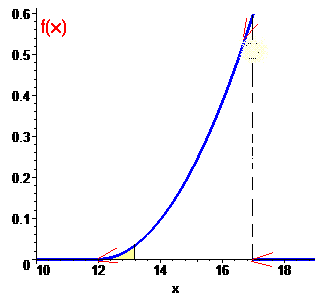
б) Математичне сподівання для неперервної величини знаходимо інтегруванням:
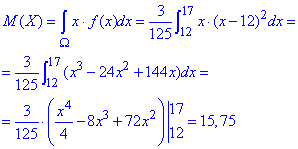
Перевіряємо значення математичного сподівання в мейплі
> M:=int(3*x*(x-12)^2/125.,x=12..17);
M := 15.75000000
Обчислюємо дисперсію за формулою:
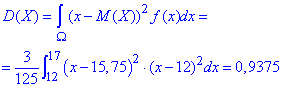
Тут теж нічого складного, підтавляємо попередньо знайдене мат. сподівання та інтегруємо.
Щоб перевірити себе, можете модифіувати попередній інтеграл в мейпл.
Результати повинні співпасти.
Середнє квадратичне відхилення прибутку як і для дискретного розподілу рівне кореню з дисперсії:
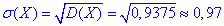
в) Ймовірність, що прибуток підприємця набуде значення з інтервалу (9 ; 13) знаходимо через інтеграл Лейбніца-Ньютона :
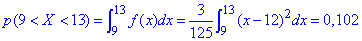
В формулі не зазначено, але ми Вам рекомендуємо перевіряти з якого моменту функція розподілу приймає ненульове значення. Якщо розібратися, то від 12, а інтервал заданий від 9. Тому перший інтервал від 9 до 12 не беремо в розгляд, а лише знаходимо визначений інтеграл на проміжку 12..13.
> int(3*(x-12)^2/125.,x=12..13);

Будьте в таких випадках уважними та завжди виконуйте перевірку.
Приклад 2 На основі показникової функції розподілу ймовірностей прибутку підприємця
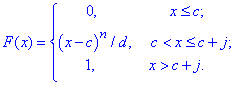
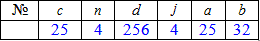
потрібно визначити:
а) щільність розподілу прибутку підприємця і нарисувати графіки функції розподілу та щільності розподілу;
б) математичне сподівання, дисперсію і середнє квадратичне відхилення прибутку підприємця;
в) ймовірність, що прибуток підприємця набуде значення з інтервалу (a ;b) .
Розв'язання: а) Записуємо функцію розподілу ймовірностей:
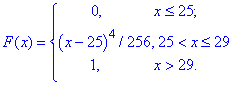
Наведемо код, який необхідний для побудови графіка в Мейплі
> q1:=plot(0,x=23..25,color=blue,thickness=3):
q2:=plot((x-25)^4/256,x=25..29,color=blue,thickness=3):
q3:=plot(1,x=29..32,color=blue,thickness=3):
> display(q1,q2,q3);
Отримаємо
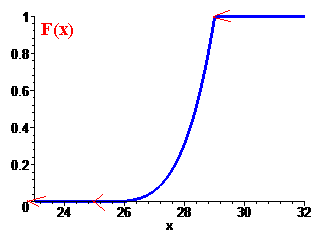
Через похідну визначаємо щільність розподілу прибутку підприємця
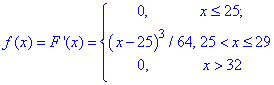
Властивості щільності розподілу (густини ймовірностей) добре розписано в попередніх матеріалах, а найкраще демонструє наступний рисунок.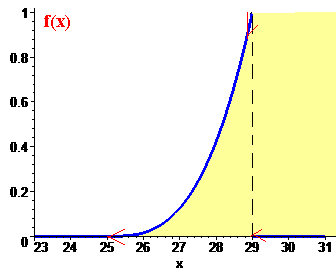
Жовтим кольором залито дуже важлива площа, суть якої пояснена в пункті в).
б) За допомогою інтегрування знаходимо математичне сподівання:
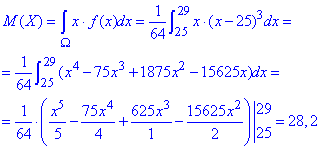
Виконуємо інтегрування в мейплі
M:=int(1*x*(x-25)^3/64.,x=25..29);
M := 28.20000000
Знаходимо дисперсію за формулою:
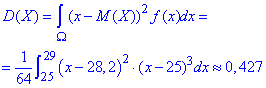
Також наводимо код, як це зробити швидко
> D:=int(1*(x-28.2)^2*(x-25)^3/64.,x=25..29);
Di := 0.4266666667
Середнє квадратичне відхилення прибутку рівне 0,65:
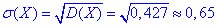
в) Ймовірність, що прибуток підприємця набуде значення з інтервалу (25 ;32) : 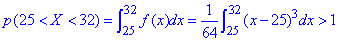
Туи немає значення наскільки більше значення за одиницю, суть лише в тому, що ящо це так то маємо 100%, що прибуто підприємця попадає в інтервал (25 ;32).
На практиці це значення рівне інтегралу від щільності розподілу, а він в свою чергу рівний площі заштрихованої (жовим) частини від (25 ;32).
Приклад 3 На основі даної функції розподілу ймовірностей прибутку підприємця
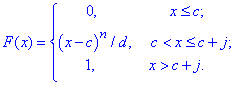
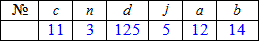
потрібно визначити:
а) щільність розподілу прибутку підприємця і нарисувати графіки функції розподілу та щільності розподілу;
б) математичне сподівання, дисперсію і середнє квадратичне відхилення прибутку підприємця;
в) ймовірність, що прибуток підприємця набуде значення з інтервалу (a;b).
Розв'язання: а) Переписуємо функцію розподілу:
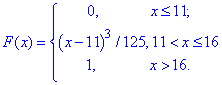
Наведемо код її побудови в математичному пакеті:
> restart;with(plots):
> q1:=plot(0,x=8..11,color=blue,thickness=3):
q2:=plot((x-11)^3/125,x=11..16,color=blue,thickness=3):
q3:=plot(1,x=16..18,color=blue,thickness=3):
> display(q1,q2,q3);
В результаті на екрані побачимо

Щільність розподілу прибутку підприємця знаходимо через похідну розподілу
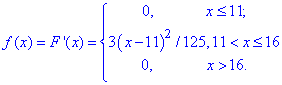
Графік щільності розподілу має вигляд

б) Інтегруванням визначаємо математичне сподівання:
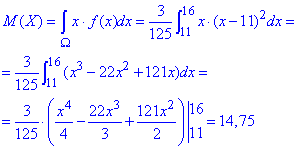
Обчислюємо дисперсію:
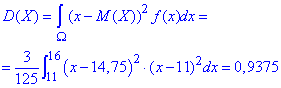
Далі знаходимо середнє квадратичне відхилення прибутку:
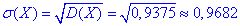
Для перевірки застосовуйте математичні пакети, які знаєте або вивчаєте в суміжних дисциплінах.
в) Ймовірність, що прибуток підприємця належатиме інтервалу (12;14) обчислимо інтегруванням: 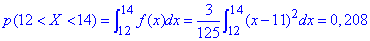
На цьому всі розрахунки до завдання.
Якщо опишете відповіді подімнич чином на індивідуальній роботі чи екзамені, то отримаєте хороші відгуки від викладача.
Приклад 4 На основі даної функції розподілу ймовірностей прибутку підприємця
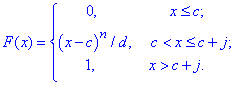
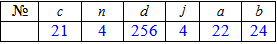
потрібно визначити:
а) щільність розподілу прибутку підприємця і нарисувати графіки функції розподілу та щільності розподілу;
б) математичне сподівання, дисперсію і середнє квадратичне відхилення прибутку підприємця;
в) ймовірність, що прибуток підприємця набуде значення з інтервалу (a ;b) .
Розв'язання: а) Функція розподілу при початковій умові рівна:
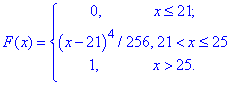
Фрагмент побудови розподілу в мейплі:
> restart;with(plots):
> q1:=plot(0,x=19..21,color=blue,thickness=3):
q2:=plot((x-21)^4/256,x=21..25,color=blue,thickness=3):
q3:=plot(1,x=25..27,color=blue,thickness=3):
> display(q1,q2,q3);
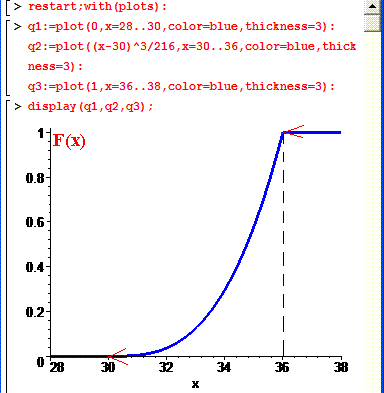
Густину ймовірностей розподілу прибутку підприємця знаходимо через похідну розподілу
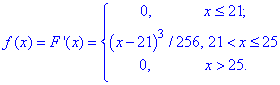
Графік густини ймовірностей має вигляд:
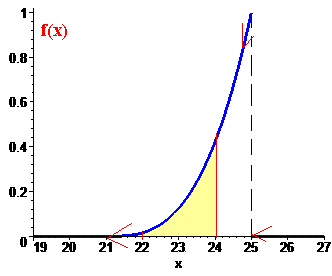
б) Знаходимо математичне сподівання:
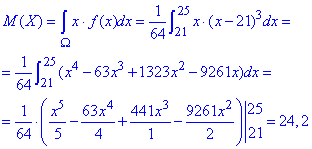
Далі дисперсію
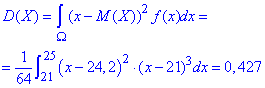
та середнє квадратичне відхилення прибутку:
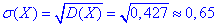
в) Ймовірність, що прибуток підприємця набуде значення з інтервалу (22 ;24) рівна 0.3125:
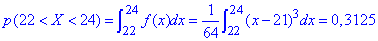
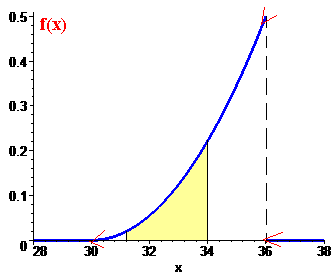
Значення знайденої ймовірності рівне площі заштрихованої на графіку щільності території.
Приклад 5 На основі даної функції розподілу ймовірностей прибутку підприємця
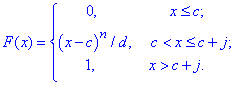
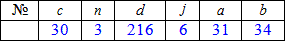
потрібно визначити:
а) щільність розподілу прибутку підприємця і нарисувати графіки функції розподілу та щільності розподілу;
б) математичне сподівання, дисперсію і середнє квадратичне відхилення прибутку підприємця;
в) ймовірність, що прибуток підприємця набуде значення з інтервалу (a ;b)
Розв'язання: а) Записуємо функцію розподілу
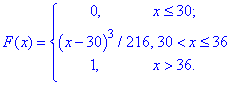
Графік функції розподілу будуємо в мейплі:
> restart;with(plots):
> q1:=plot(0,x=28..30,color=blue,thickness=3):
q2:=plot((x-30)^3/216,x=30..36,color=blue,thickness=3):
q3:=plot(1,x=36..38,color=blue,thickness=3):
> display(q1,q2,q3);
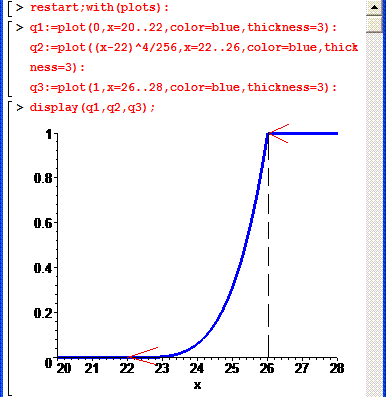
Через похідну визначаємо щільність розподілу прибутку підприємця
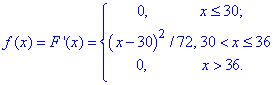
ЇЇ графік наступний
б) Математичне сподівання:
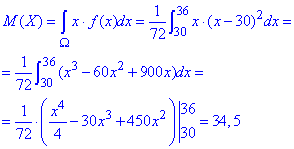
Дисперсія:
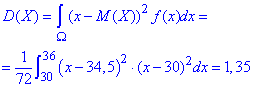
Середнє квадратичне відхилення прибутку:
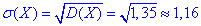
в) Ймовірність, що прибуток належить інтервалу (31;34) рівна 0.292: 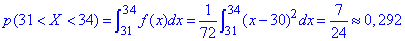
Як можна переконатися, усі числові характеристики розподілів вимагають добрих вмінь інтегрувати.
Приклад 6 На основі функції розподілу
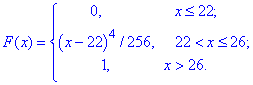
ймовірностей прибутку підприємця потрібно визначити:
а) щільність розподілу прибутку підприємця і нарисувати графіки функції розподілу та щільності розподілу;
б) математичне сподівання, дисперсію і середнє квадратичне відхилення прибутку підприємця;
в) ймовірність, що прибуток підприємця набуде значення з інтервалу (a;b).
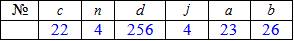
Розв'язання: а)Вионуємо побудову графіка функції розподілу:
> restart;with(plots):
> q1:=plot(0,x=20..22,color=blue,thickness=3):
q2:=plot((x-22)^4/256,x=22..26,color=blue,thickness=3):
q3:=plot(1,x=26..28,color=blue,thickness=3):
> display(q1,q2,q3);

Щільність розподілу на краях рівна нулю, а на середньому інтервалі похідній розподілу
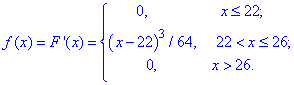
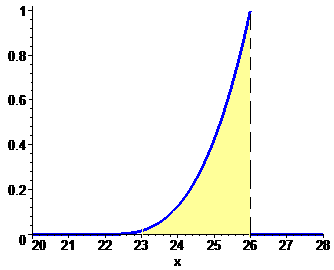
Графік щільності розподілу має вигляд
б) Інтегруванням знаходимо математичне сподівання:
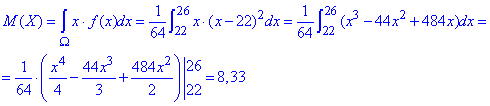
Далі дисперсію:

та останню ймовірнісну характеристику:
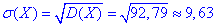
в) Ймовірність, що прибуток підприємця набуде значення з інтервалу (23;26) рівна 0.996: 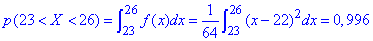
Ймовірність попадання в інтервал знаходимо в мейплі
int((x-22)^3/64.,x=23..26);

Значення відповідає заштрихованій вище ділянці на графіку щільності ймовірностей. Так як щільність починає зростати від 22, а інтеграл беремо від 23 то його значення не дотягує до одиниці.
Використовуйте наведений алгоритм розрахунків, він легкий для запам'ятовування і вимагає знання однієї формули з інтегрування.
Збережіть сторінку в закладки, якщо інформація допомогла Вам в навчанні.
Попереду Вас ще чекає чимало готових відповідей з ймовірності!


