Функція розподілу ймовірностей дискретної величини

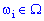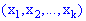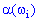Розглянемо простір елементарних подій, в якому кожній елементарній події у відповідність ставиться число x або вектор , тобто на множині є певна функція , яка для кожної елементарної події 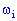знаходить елемент одновимірного простору R₁ або n - вимірного простору R_n.

Цю функцію називають випадковою величиною. У випадку, коли 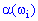відображає множину на одновимірний простір R₁, випадкову величину називають одновимірною. Якщо відображення здійснюється на R_n, то випадкову величину називають n -вимірною (системою n випадкових величин або n -вимірним випадковим вектором).

Величина називається випадковою, якщо внаслідок проведення досліду під впливом випадкових факторів вона набуває того чи іншого можливого числового значення з певною ймовірністю.

Якщо множина можливих значень випадкової величини є зліченною, то її називають дискретною. У протиежному випадку її називають неперервною.

Випадкові величини для зручності позначають великими літерами латинського алфавіту X, Y, Z,..., а їх можливі значення – малими x, y, z,....

Для встановлення випадкової величини необхідно знати не лише множину можливих її значень, а й вказати, з якими імовірностями вона набуває того чи іншого можливого значення.

З цією метою вводять поняття закону розподілу ймовірностей – залежність, що встановляє зв'язок між можливими значеннями випадкової величини та відповідними їм імовірностями.

Закон розподілу дискретної випадкової величини найчастіше задають в табличній формі, функцією, або графічно за допомогою ймовірнісного многокутника.

У разі табличної форми запису закону вказується множина можливих значень випадкової величини X розміщена у порядку їх зростання в першому рядку, та відповідних їм імовірностей в наступному:

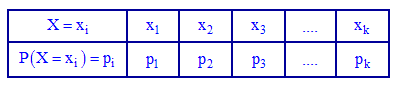
Випадкові події мають бути попарно несумісними та утворювати повну групу, тобто задовільняти умову:

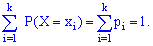
Наведену залежність називають умовою нормування для дискретної випадкової величини X, а таблицю розподілу – рядом розподілу.

Функція розподілу ймовірностей та її властивості

Закон розподілу ймовірностей можна подати у вигляді функції розподілу ймовірностей випадкової величини F(x), яка вже придатна як для дискретних, так і для неперервних випадкових величин

Функцію аргументу x, що встановлює ймовірність випадкової події X<x називають функцією розподілу ймовірностей:Її слід розуміти як функцію, яка встановлює ймовірність випадкової величини, яка може приймати значення, менші за x .

Функція розподілу володіє наступними властивостями:

1. Вона завжди додатня із значеннями в межах від нуля до одиниці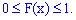

2. Функція є монотонно зростаючою, а саме значення функції зростають 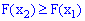, якщо аргументи зротають x₂>x₁.

Із цієї властивості отримують наведені висновки:
a) Імовірність набуття випадковою величиною X можливих значень з проміжку рівна приросту її інтегральної функції F(x) на цьому проміжку:
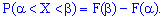б) Імовірність, що неперервна випадкова величина X набуде конкретного можливого значення, завжди дорівнює нулю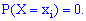Для неперервної випадкової величини справджуються такі рівності: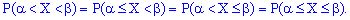3. На крайніх точках неперервна випадкова величина приймає значення.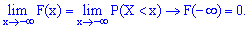
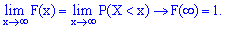
Із цих границь випливає, що для дискретної випадкової величини X з можливими значеннями з обмеженого проміжку [a;b] маємо

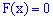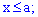
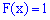для
для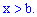

Наведемо розв'язки задач на відшукання функції розподілу.

Приклад 1. Закон розподілу дискретної випадкової величини Х задано таблицею:

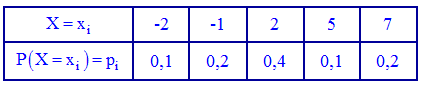
Побудувати функцію розподілу F(x) та її графік.

Розв'язання. Згідно з властивостями функції F(x) отримаємо наведені дальше значення.
1)
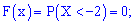
2)
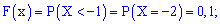
3)
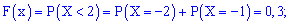
4)
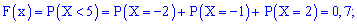
5)
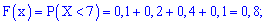
6)
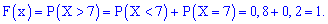
Компактно F(x) матиме запис

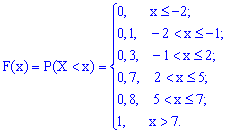
Графік функції F(x) зображено на рисунку нижче

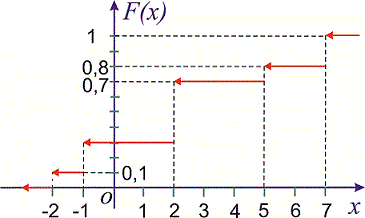
функція розподілу
Наведений аналіз є повною відповіддю до завдання.

Приклад 2. Маємо три коробки з кульками. У першому міститься 6 жовтихих і 4 сині кульки, у другому – 7 жовтиих і 3 сині, а в третьому — 2 жовті і 8 синіх. Із кожної коробки навмання беруть по одній кульці. Побудувати закон розподілу ймовірностей дискретної випадкової величини X – появи числа синіх кульок серед трьох навмання взятих; визначити закон розподілу F(x) та побудувати графік цієї функції.

Розв'язання. Серед трьох навмання взятих кульок число синіх може бути 0; 1; 2; 3.
У табличній формі закон розподілу дискретної випадкової величини має вигляд:

Обчислимо ймовірності p₁, p₂, p₃, p₄. Із цією метою позначимо A₁ випадкову подію, що полягає відповідно в появі жовтої кульки і B₁ – появі синьої з першої коробки. Подібним чином для решти коробок A₂, B₂, A₃, B₃. Імовірності цих подій такі:

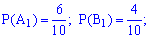
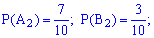
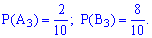
Оскільки випадкові події A₁, B₁, A₂, B₂, A₃, B₃ є незалежними, то ймовірності знаходимо за формулами:

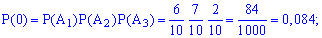
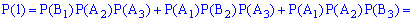
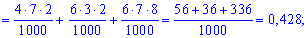
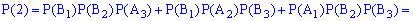
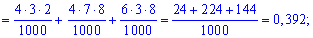
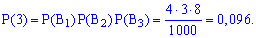
Обчислення достатньо прості і зроблені позначення повністю все пояснюють. Перевіримо виконання умови нормування

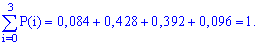
Завжди виконуйте перевірку даної умови: це достатньо просто зробити та дозволяє швидко перевірити правильність обчислень ймовірності. У випадках, коли умова нормування не виконується потрібно відшукати помилку та виправити її.
У нас же всі обчислення правильні, тому записуємо закон розподілу ймовірностей в табличній формі:

Обчислюємо значення інтегральної функції
1)
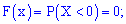
2)
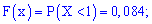
3)
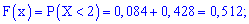
4)
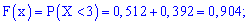
5)
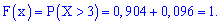
У випадку помилок при знаходженні ймовірностей останнє співвідношення дає відмінни від одиниці результат, тому можете перевіряти і за цим значенням. Спрощено функція розподілу матиме вигляд

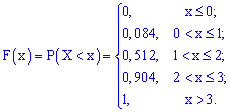
а її графік наступний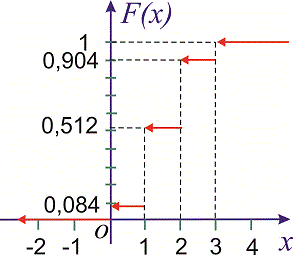 графік функції розподілу

Приклад 3. Закон розподілу неперервної випадкової величини X задано функцією розподілу ймовірностей

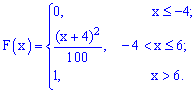
Побудувати графік функції розподілу F(X) і обчислити ймовірність, що випадкова величина належить проміжку P(1<X<4).

Розв'язання. Функція розподілу матиме вигляд.

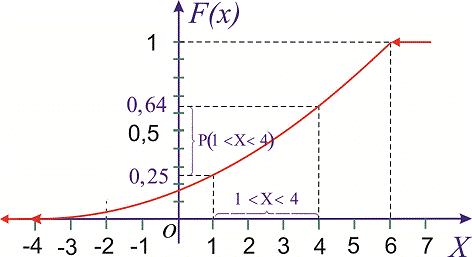
інтегральна фунція розподілу

Використовуючи означення, обчислимо
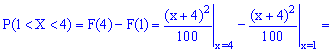
інтеграьна функція розподілу

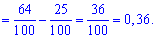
Таким чином ймовірність, що випадкова величина належить проміжку [1,4] рівна 0,36.

Уважно розберіться з наведеними прикладами знаходження функції розподілу, це Вам стане в нагоді на практичних заняттях. Старайтеся перевіряти умову нормування, щоб уникнути подальших помилок і правильно визначайте ймовірності.