Далі наведені задачі на встановлення закону розподілу та функції розподілу випадкових величин, ймовірності появи яких загалом невідомі, а лише описані загальною умовою. Завдання полягає у знаходженні закономірностей випадкових величин, визначенні математичного сподівання, дисперсії та інших статистичних характеристик. Кожне із завдань охоплює кілька тем теорії ймовірності, включаючи визначення та побудову відповідних законів розподілу. Відповіді добре обгрунтовані формулами, тож переходимо до аналізу методики розрахунків.
Приклад 1 В урні n=10 кульок, з яких m=5 білих, а решта чорні.
З цієї урни навмання виймають k=5 кульок.
Потрібно знайти:
- а) закон розподілу дискретної випадкової величини X, рівній числу вийнятих чорних кульок;
- б) функцію розподілу випадкової величини X та побудувати її графік;
- в) математичне сподівання випадкової величини X;
- г) дисперсію і середнє квадратичне відхилення випадкової величини X;
- д) ймовірності попадання в інтервали
 , X>b, X<a.
, X>b, X<a.

Пункти а)-г) в кожному із завдань повторюється тому їх дальше наводити не будемо.
В інтернеті можна знайти ще безліч завдань в основному на біноміальний, рівномірний та гіпергеометричний розподіли.
Розв'язання: а) Ймовірність Pk того, що навмання виймають z чорних кульок з 5 обчислимо за формулою:
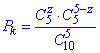
де z – кількість витягнутих чорних кульок.
Чому саме така залежність для ймовірності детально розписано в статті про кульки.
Загалом ймовірність змінюється за формулою гіпергеометричного розподілу.
Результати обчислень запишемо в таблицю:
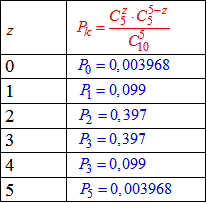
Загалом тут буде пояснено сам хід обчислень, детальні обчислення зі спрощенням факторіалів Вам мають бути знайомі.
Формули сполучень з повтореннями та без них на момент вивчення теми Вам мають бути знайомі, інакше слід починати з основ комбінаторики і переглянути базовий матеріал.
На основі таблиці закону розподілу виконуємо побудову графіка
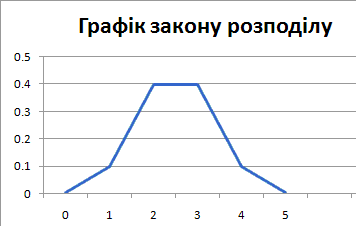
В Вас він повинен виглядати подібно, незалежно від того в чому виконуєте побудову.
б) Функцію розподілу випадкової величини X знайдемо за формулою
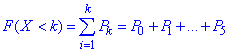
Детальніше про її властивості та фізичний зміст Ви можете ознайомитися за наведеним вище посиланням.
Для дискретно розподіленої випадкової величини функція розподілу рівна сумі попередніх ймовірностей, для неперервної випадової величини - інтегралу з верхньою обмеженою границею.
Результати запишемо в таблицю:
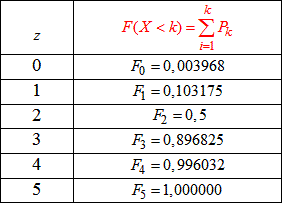
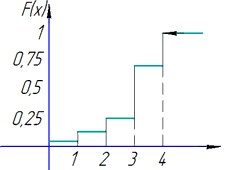
Далі будуємо графік функції розподілу
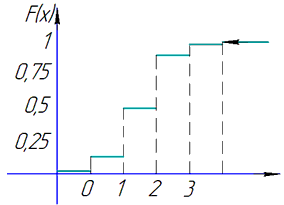
Для дискретних випадкових величин вона має вигляд "сходин". На цьому типовий приклад, який може чекати Вас на модулі чи заліку обчислено.
Переходимо до інших типових завдань на розподіли випадкових величин
Приклад 2 Ймовірність того, що витрати електроенергії на підприємстві протягом дня не будуть перевищувати норми, дорівнює p=0,9.
Нехай 8 - кількість днів, протягом яких працює підприємство, а X- кількість днів, протягом кожного з яких витрати електроенергії не будуть перевищувати норми.
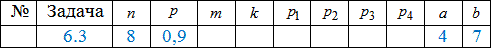
Розв'язання: а) Оскільки від досліду до досліду ймовірність залишається сталою (а саме p=0.9 і q=1-p=0.1), то ймовірність того, що витрати електроенергії на підприємстві протягом дня не будуть перевищувати норми з кожним днем знайдемо із залежності:
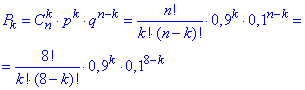
Результати запишемо в таблицю:
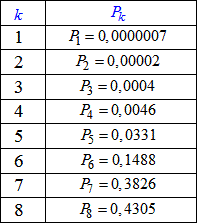
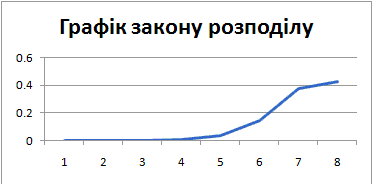
Графік закону розподілу матиме вигляд
б) Функцію розподілу випадкової величини X знайдемо за формулою суми
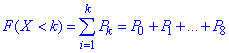
Результати сумування ймовірностей записуємо в таблицю:
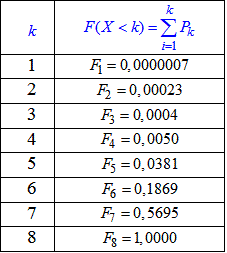
Графік функції розподілу має вигляд
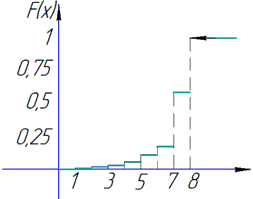
в) Математичне сподівання випадкової величини
M(X)=n•p=8•0.9=7.2
г) Дисперсія D(X)=n•p•q=8•0.9•0.1=0.72
Середнє квадратичне відхилення випадкової величини X:
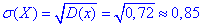
д) Ймовірності попадання в інтервали випадкової величини X
Xє[4;7] (від 4 до 7 разів включно):
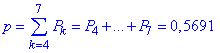
X>7 (8 разів):
p=P8=0.4305;
X<4 (від 1 до 3 разів):
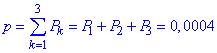
Ось і всі розрахунки входження випадкових величин в інтервали.
Приклад 3 Робітник обслуговує 4 незалежно працюючих верстати. Ймовірність того, що протягом години станок не буде потребувати уваги робітника, дорівнює для першого верстата p1=0,6, для другого – p2=0,7, для третього – p3=0,8 , для четвертого – p4=0,9. Знайти характеристики розподілу.

Розв'язання: а) Ймовірність Pk того, що протягом години кількість верстатів не буде потребувати уваги робітника, обчислюємо, як і в задачі 3, тобто таким чином pk – ймовірність, що k-й верстат не потребує уваги робітника.
qk=1-pk – ймовірність, що k-й верстат потребує уваги робітника.
P0=q1•q2•q3•q4 – для жодного верстату не треба уваги робітника;
P1=p1•q2•q3•q4+q1•p2•q3•q4+... – для одного верстату;
P2=p1•p2•q3•q4+q1•p2•p3•q4+... – для 2-х верстатів;
P3=p1•p2•p3•q4+p1•p2•q3•p4+p1•q2•p3•p4+q1•p2•p3•p4 – для 3-х верстатів;
P4=p1•p2•p3•p4 – для всіх верстатів не треба уваги робітника.
Результати обчислень запишемо в таблицю:
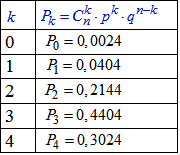
Будуємо графік закону розподілу
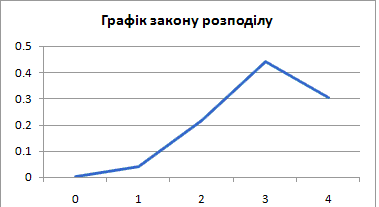
б) Функцію розподілу випадкової величини X знайдемо за формулою
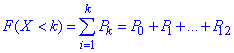
Результати сум записуємо в таблицю:
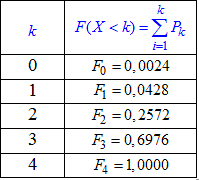
Графік функції розподілу наведено далі
в) Математичне сподівання випадкової величини 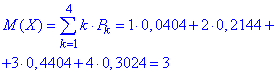
г) Дисперсія
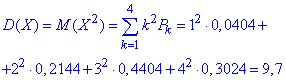
Середнє квадратичне відхилення випадкової величини X:
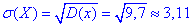
д) Ймовірності попадання в інтервали випадкової величини X
Хє[1;3] (від 1 до 3 разів включно):
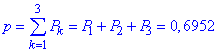
X>3 (4 рази):
p=P4=0.3024
X<1 (0 раз):
p=P0=0.0024.
Для двомірного випадку, коли маємо систему двох випадкових величин (X,Y) також встановлюють закони розподлу однєї з величин.
Завдання 3.2 Задано закон розподілу системи випадкових величин (X,Y).
Y \ X | -1 | 2 | 3 |
-3 | 0,1 | 0,3 | 0,2 |
3 | 0,1 | 0,15 | 0,15 |
Знайти закон розподілу випадкової величини X.
Розв'язування: Запишемо розподіл X (pi відповідає сумі ймовірностей кожного стовпчика):
Y \ X | -1 | 2 | 3 |
-3 | 0,1 | 0,3 | 0,2 |
3 | 0,1 | 0,15 | 0,15 |
Перевірка: ∑pi=0,2+0,45+0,35=1.
Як бачите завдання не складні і їх під силу вирішити кожному. Знаходження законів розподілу для неперервних випадкових величин розглянемо в наступних публікаціях, для їх відшукання Ви повинні добре вміти інтегрувати. Якщо Вам важко написати модуль чи підсумкову контрольну самостійно, то ми готові Вам допомогти! Для цього зробіть замовлення та очікуйте на відповіді з поясненнями.


