Однією з часто використовуваних на практиці характеристик при аналізі випадкових величин є математичне сподівання. Під даним терміном часто вживають "середнє значення" випадкової величини X. Розраховувати його не так важко, особливо якщо маємо дискретну величину з невеликою кількістю точок.
Математичним сподіванням дискретної випадкової величини X називається величина, яка рівна сумі попарних добутків величин x[i] на їх ймовірності появи p[i]
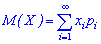 Якщо множина обмежена, то потрібно шукати суму скінченного числа доданків
Якщо множина обмежена, то потрібно шукати суму скінченного числа доданків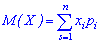 Якщо множина X є неперервною, то математичне сподіванням неперервної випадкової величини X визначається інтегруванням за формулою
Якщо множина X є неперервною, то математичне сподіванням неперервної випадкової величини X визначається інтегруванням за формулою
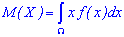 Якщо множина нескінченна
Якщо множина нескінченна 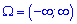 , то
, то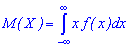
Якщо неперервна величина задана на інтервалі 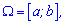 то математичне сподівання рівне
то математичне сподівання рівне 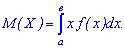
Властивості математичного сподівання
1. Математичне сподівання від сталої величини C рівне сталій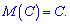 2. Сталий множник при випадковій величині можна виносити за дужки
2. Сталий множник при випадковій величині можна виносити за дужки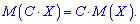 Для дискретної випадкової величини справедлива залежність
Для дискретної випадкової величини справедлива залежність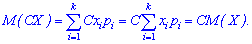 Для неперервної наступна:
Для неперервної наступна: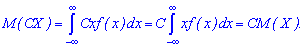 3. Якщо A і B є сталими величинами, то справедлива залежність
3. Якщо A і B є сталими величинами, то справедлива залежність
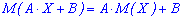
Для дискретної випадкової величини:
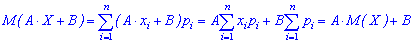
Для неперервної випадкової величини:
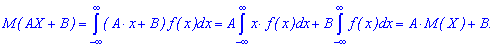
Наведемо розв'язки поширених на практиці задач.
Приклад 1. Закон розподілу дискретної випадкової величини задано таблично: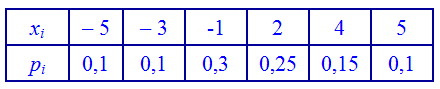 Обчислити математичне сподівання.
Обчислити математичне сподівання.
Розв'язання. Згідно наведеної вище формули, обчислюємо
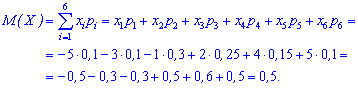
Таким чином, знайдене математичне сподівання рівне M(x)=0,5.
Приклад 2. За заданою функцією щільності ймовірностей
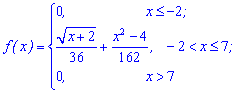
обчислити математичне сподівання.
Розв'язання. Згідно формули для неперервної випадкової величини проводимо інтегрування
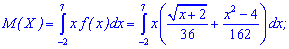
попереднто розбивши на два інтеграли
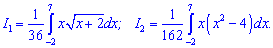
Знайдемо їх значення по черзі, для першого необхідно виконати заміну змінних
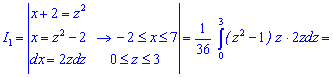
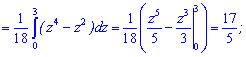
Другий інтеграл досить простий
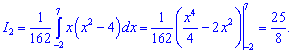
Вкінці обислюємо їх суму
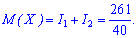
Приклад 3. Щільність імовірностей задано тригонометричною формулою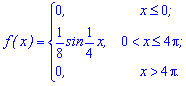 Знайти математичне сподівання.
Знайти математичне сподівання.
Розв'язання. Проводимо інтегрування частинами
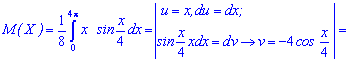
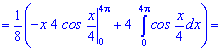
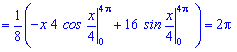
Знайдене математичне сподівання рівне 2*Pi
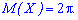
Приклад 4. За заданою функцією розподілу ймовірностей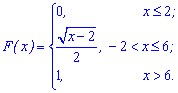 обчислити математичне сподівання.
обчислити математичне сподівання.
Розв'язання. Для обчислення M(x) необхідно спочатку знайти щільність імовірностей. Для цього здійснюємо диференціювання функції розподілу
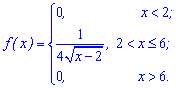
Після цього проводимо інтегрування за відомою вже формулою:
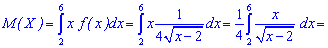
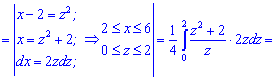
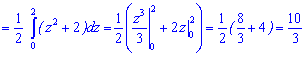
При обчисленні ітегралу довелося робити заміну змінних. Будьте в таких випадках уважними, заміна змінних у визначених інтегралах завжди приводить до зміни меж інтегрування.
Математичне сподівання рівне 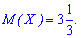
Для перевірки правильності обчислень запам'ятайте, що якщо випадкова величина належить проміжку 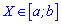 , то математичне сподівання M(x) також повинно знаходитися всередині [a; b], виконуючи роль центра розподілу цієї величини. У випадках коли знайдене математичне сподівання виходить за межі проміжку потрібно проаналізувати попередні обчислення і виправити помилки. Будьте уважними при інтегруванні функцій та заміні змінних, саме в цьому прихована левова частка Ваших помилок .
, то математичне сподівання M(x) також повинно знаходитися всередині [a; b], виконуючи роль центра розподілу цієї величини. У випадках коли знайдене математичне сподівання виходить за межі проміжку потрібно проаналізувати попередні обчислення і виправити помилки. Будьте уважними при інтегруванні функцій та заміні змінних, саме в цьому прихована левова частка Ваших помилок .


