підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
1 Варіант
Приклад 164. Яка ймовірність того, що при одному киданні грального кубика випаде число очок, що дорівнює:
1) двом;
2) п'яти;
3) парному числу;
4) числу, яке кратне 6?
Розв'язання:
За значенням ймовірність рівна відношенню кількості сприятливих подій до кількості всіх подій.
1) Кубик має 6 сторін з кількістю точок від 1 до 6. Грань, що відповідає випадінню двійки всього одна. Звідси ймовірність першої події рівна
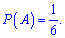
2) Таку саму ймовірність отримаємо при випадінні п'ятірки (подія ідентична до випадіння двійки)
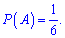
3) Парні числа 2;4;6, це значить , що сприятливих подій буде половина від всіх, а ймовірність визначається залежністю
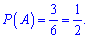
4) Кратне числу 6 одне значення 6, отже ймовірність наступна
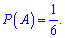
Відповідь: 1/6; 1/6; 1/2; 1/6.
---====================---
Приклад 165. Щоб здати екзамен з математики, треба вивчити 30 білетів. Учень вивчив на відмінно 25 білетів. Яка ймовірність того, що, відповідаючи на один білет, він отримає відмінну оцінку?
Розв'язання:
Нехай подія А полягає в тому, що учень отримає відмінну оцінку, тоді
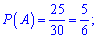
Відповідь: 5/6.
---====================---
Приклад 166. У гральній колоді 36 карт. Навмання вибирається одна карта. Яка ймовірність того, що ця карта:
1) туз;
2) червовий туз?
Розв'язання:
1) У колоді 4 тузи, тоді ймовірність вибору туза рівна
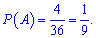
2) Червовий туз один, відповідно ймовірність буде
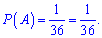
Відповідь:1/9; 1/36.
---====================---
Приклад 167. Кидають дві однакові монетки. Яка ймовірність того, що випадуть:
1) два герба;
2) герб і цифра?
Розв'язання:
1) Випадання герба і цифри є рівноймовірними подіями. Тому ймовірність появи герба, як і цифри, рівна 0, 5.
В першому випадку ймовірності потрібно перемножити
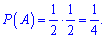
2) В другому маємо правильну послідовність подій, вони чергуються за нормальним законом, тому ймовірність рівна
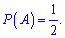
---====================---
Приклад 168. Яка ймовірність того, що ваша майбутня дитина народиться:
1) 7 числа;
2) 31 числа;
3) 29 числа?
Розв'язання:
Для знаходження відповіді потрібно мати перед очима календар. З нього шукаємо всі сприятливі події серед випадкових.
1) Припустимо, що в році 365 днів. З них в кожному місяці (таких 12) маємо 7 число, тобто ймовірність рівна
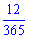 або
або
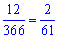
якщо рік високосний.
2) В році 7 місяців має число 31, відповідно ймовірність події
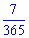 або
або 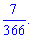
3) І всі місяці крім січня (11) мають 29 число, тому ймовірність рівня 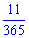 або
або 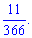
На цьому всі ймовірності знайдено, переходимо до наступного завдання.
---====================---
Приклад 169. У ящику знаходилося 45 кульок, з яких 17 білих. Загубили дві не білих кульки. Яка ймовірність того, що вибрана навмання одна кулька буде білою?
Розв'язання:
За умовою в ящику мали 45 кульок, дві – загубили, отже стало 45-2=43;
Подія А полягає в тому, що вибрана навмання кулька буде білою, тоді ймовірність рівна
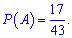
Відповідь: 17/43.
---====================---
Приклад 170. У коробці лежать 5 червоних, 8 синіх, 3 зелених і 4 жовтих кульки. З коробки навмання витягли одну кульку. Яка ймовірність того, що ця кулька не буде синьою?
Розв'язання: Всього в коробці 5+8+3+4=20.
Синіх кульок 8, решта кольорів 20-8=12, тоді ймовірність знаходимо діленням
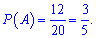
Відповідь: 3/5.
---====================---
Приклад 171. Яка ймовірність того, що навмання вибране двоцифрове число ділиться націло на 12?
Розв'язання: Всього двоцифрових чисел 90 (10..99) , на 12 ділиться наступні:12; 24; 36; 48; 60; 72; 84; 96. Відповідно маємо m=8 сприятливих подій і n=90 загальну їх кількість.
Тоді ймовірність визначається залежністю
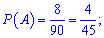
Відповідь: 4/45.
-------------------------------------------------------------
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Біном Ньютона. №158-163
- Наступні відповіді - Обчислення ймовірностей за допомогою правил комбінаторики
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!



