 Посібник для підготовки до ЗНО тестування з МАТЕМАТИКИ
Посібник для підготовки до ЗНО тестування з МАТЕМАТИКИ
Підручник для 9-11 класів:
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Завантажити (скачати) відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики). Формат: PDF
Зміст: Посібник містить поради щодо проходження ЗНО з математики та взірці тестових завдань. Усі задачі однієї теми розміщені в порядку складності.
Рекомендуємо всім завантажити відповіді до ЗНО та самостійно пройти теми, з якими маєте труднощі на практичних.
Рік випуску: 2010 р.
Тема 30: Прямокутний трикутник
На попередньому занятті наведені готові відповіді перших 16 задач на прямокутні трикутники. Далі розберемо ще 9 прикладів, які можуть чекати Вас на ЗНО тестах.
Інструкції та формули, що тут містяться, не важкі, тому вважаємо що значна їх частина Вам відомо з тригонометрії і не потребує додаткових пояснень.
У разі труднощів в обчисленні подібних задач можете звертатися до нас за допомогою.
Завдання 30.17 У прямокутному трикутнику один з гострих кутів дорівнює 32.
Знайти кут між висотою і медіаною, проведеними з вершини прямого кута.
Обчислення: Виконуємо побудову трикутника до задачі
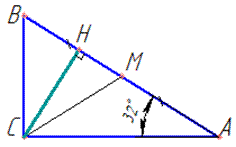
За побудовою CH- висота трикутнику ABC (<ACB=90),
CM - медіана, тому MB=MA;
MB=HB+HM, звідси HB+HM=HA-HM.
Маємо <A=32 за умовою, тоді <B=90-< A=90-32=58.
Нехай <MCH=x – кут між медіаною і висотою у трикутнику ABC.
Звідси <BCH=32, < ACH=58.
Розглянемо трикутник MCH (<CHM=90):
HM=CH·tg(x) (тут HM і CH відповідно протилежний і прилеглий катети у ΔMCH).
Розглянемо трикутник ACH (<AHC=90):
HA=CH·tg(58) (тут HA і CH відповідно протилежний і прилеглий катети в ΔACH).
Розглянемо трикутник BCH (<BHC=90):
HB=CH·tg(32) (тут HB і CH відповідно протилежний і прилеглий катети у ΔBCH).
Підставимо отримані вирази у рівність HB+HM=HA-HM:
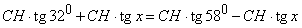
Скоротивши останню рівність на CH і розв'язавши рівняння, знайдемо x:
Розв'язок рівняння:
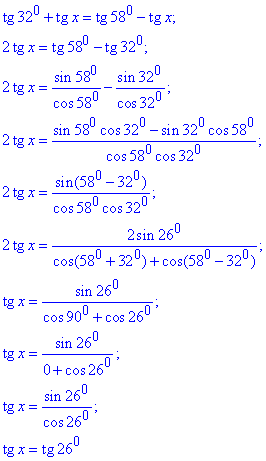
оскільки у трикутнику 0< x<90, то x=26.
Необхідні формули тригонометрії (для довільного кута α):
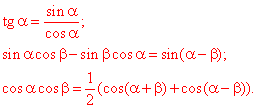
Відповідь: 260 – Б.
Цю задачу можна було розв'язати, за допомогою теореми: «кут між висотою та медіаною прямокутного трикутника, що проведені з вершини прямого кута, дорівнюють подвійному куту між бісектрисою і висотою трикутника, опущеного з вершини прямого кута».
Як шукати кут між бісектрисою і висотою прямокутного трикутника показано в задачі 30.16.
Завдання 30.18 Бісектриса прямого кута прямокутного трикутника поділяє гіпотенузу на відрізки у відношенні 3:4.
У якому відношенні ділить гіпотенузу висота?

Обчислення: Виконуємо додаткову побудову до задачі
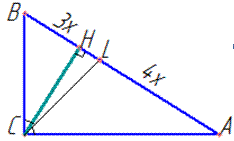
У прямокутному трикутнику ABC (< ACB=90) CH - висота,
CL - бісектриса;
AL+4x, BL=3x, оскільки BL:AL=3:4 (за умовою), де x - коефіцієнт пропорційності між AL і BL.
У будь-якому трикутнику бісектриса ділить протилежну сторону пропорційно бічним сторонам, звідси маємо AC+4xy, BC=3xy,
де y - коефіцієнт пропорційності між AC і BC.
За теоремою Піфагора складемо рівність між сторонами ΔABC:
AB^2=AC^2+BC^2, тут AB=AL+BL=4x+3x=7x, звідси
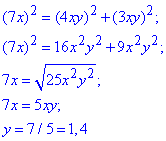
Отож, AC=5,6x і BC=4,2x.
Знайдемо висоту ΔABC:
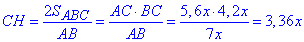
Висота ΔBHC (< BHC=90) маємо
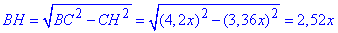
Для ΔAHC (< AHC=90) за теоремою Піфагора знаходимо
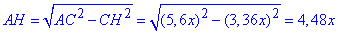
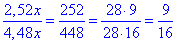
Звідси отримаємо відношення:
BH/AH=2,52x/4,48x=9/16.
Відповідь: 9:16 – В.
Завдання 30.19 Знайти площу прямокутного трикутника, у якого бісектриса прямого кута ділить гіпотенузу на відрізки завдовжки 4 см і 8 см.
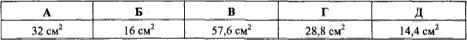
Обчислення: Позначимо через CH - висоту прямокутного трикутника ABC (< ACB=90),
CL - бісектриса;
AL=8 см, BL=4 см, звідси BL:AL=1:2.
Схематичний рисунок має вигляд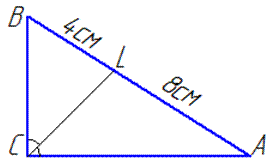
У будь-якому трикутнику бісектриса ділить протилежну сторону пропорційно бічним сторонам, звідси маємо AC=x, BC=2x, де x - коефіцієнт пропорційності між сторонами AC і BC. За теоремою Піфагора складемо рівність між сторонами ΔABC:
AB^2=AC^2+BC^2, тут AB+AL+BL=8+4=12 см, звідси
12^2=x^2+(2x)^2,
144=x^2+4x^2,
5x^2=144,
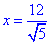 см.
см.
Катети трикутника рівні
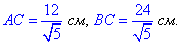
Знайдемо площу ΔABC:
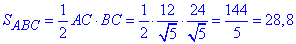 см2.
см2.
Відповідь: 28,8 см2 – Г.
Завдання 30.20 Гіпотенуза прямокутного трикутника дорівнює 10 см.
Якою найбільшою може бути площа трикутника?

Обчислення: Щоб площа прямокутного трикутника була максимальною, треба щоб довжини катетів були рівними, тобто a=b.
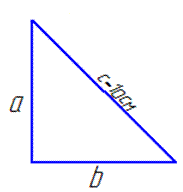
Тоді за теоремою Піфагора маємо:
c^2=a^2+b^2,
c^2=a^2+a^2,
c^2=2a^2,
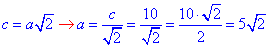 см.
см.
Отож, 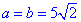 см.
см.
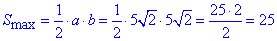 см2.
см2.
Відповідь: 25 см2 – Г.
Завдання 30.21 На сторонах прямокутного трикутника ABC (<C=900) побудовані квадрати.
Площа квадрата, побудованого на гіпотенузі, дорівнює 400 см2,
а різниця площ квадратів, побудованих на катетах, дорівнює 112 см2.
Знайти площу трикутника.
Обчислення: Допоміжний малюнок до задачі має вигляд
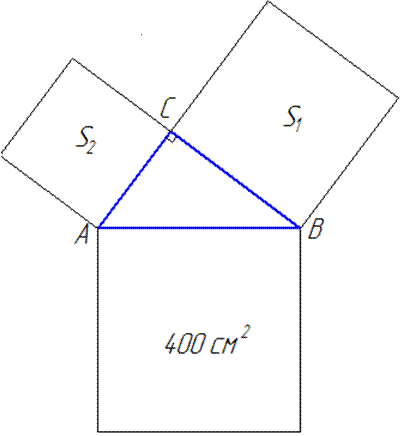
Нехай AB – сторона квадрата загальною площею S=400 см2.
Тобто S=AB^2, тобто AB^2=400, звідси AB=20 см – гіпотенуза прямокутного ΔABC.
Звідси слідує, що сторони квадратів, побудованих на катетах цього ж трикутника є довжинами цих катетів, тобто S1=a^2 і S2=b^2.
За умовою задачі S1-S2=112 см2, тобто a^2-b^2=112.
За теоремою Піфагора маємо:
a^2+b^2=20^2, тобто a^2+b^2=400.
Маємо два рівняння з двома невідомими a і b, запишемо рівняння у систему і знайдемо довжини катетів:
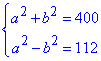
2a^2=512,
a^2=256,
звідси a=16 см.
Підставляємо в перше рівняння
256+b^2=400,
b^2=144,
звідси b=12 см.
Знайдемо площу ΔABC:
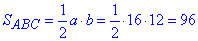 см2.
см2.
Відповідь: 96 см2 – В.
Завдання 30.22 На рисунку зображено прямокутний трикутник ABC (<C=90), його висоту CH, медіану CM і позначено величини деяких його елементів.
Установити відповідність між елементами трикутника (1–4) та їхніми величинами (А–Д). 
Обчислення: Знайдемо кут між висотою і бісектрисою прямокутного трикутника (див. рисунок):
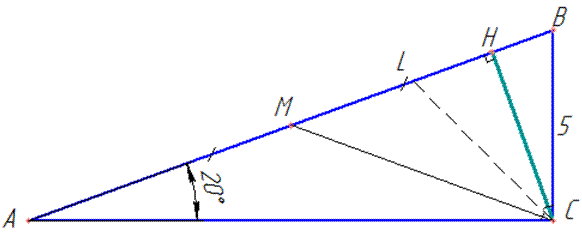
У прямокутному трикутнику ABC (<C=90) CH - висота, CL - бісектриса, тому < ACL=< C:2=45.
Розглянемо трикутник ACH (< AHC=90), < CAH=20 за умовою.
За теоремою про суму кутів трикутника ACH знайдемо < ACH:
<ACH=180-(<AHC+<CAH)=180-(90+20)=70.
Знайдемо кут <HCL – кут між висотою і бісектрисою трикутника ABC:
<HCL=<ACH-<ACL=70-45=25.
1) Знайдемо <MCH – між медіаною і висотою прямокутного трикутника.
Він рівний подвоєному куту між висотою і бісектрисою цього ж трикутника, опущеними з вершини прямого кута, тобто
<MCH=2·<HCL=2·25=50 – В.
2) Знайдемо <CMH за теоремою про суму кутів трикутника CMH:
<CMH=180-<MCH-<MHC=180-50-90=40 – Д.
4) Знайдемо CH у прямокутному трикутнику BHC (<BHC=90) і <BCH=20:
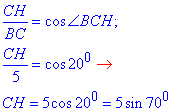 – Г.
– Г.
3) Знайдемо CM у прямокутному трикутнику MHC (<MHC=90) і <MHC=50:
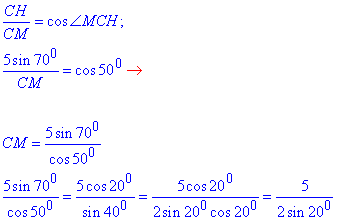
Таким чином
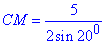 – А.
– А.
Тут використали наступні формули зведення:
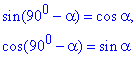
Завдання 30.23 У прямокутному трикутнику ABC (<C=90) проведено бісектрису CK та висоту CH.
Установити відповідність між значеннями кута при вершині A (1–4) та, розміщеній зі сторони бісектриси, і кутом KCH (А–Д).
1. 80
2. 320
3. 280
4. 180
А. 270
Б. 330
В. 370
Г. 130
Д. 170
Обчислення: Побудуємо трикутник до задачі
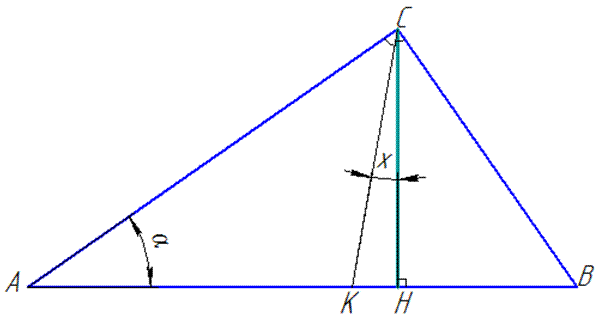
Нехай <A=α (задано в умові задачі для 1 – 4 пунктів) і <KCH=x. Тоді, використовуючи теоремо про суму кутів трикутника, встановлюємо:
<B=90-α, <BCH=α, <BCK=α+x, <KCH=90-x.
Так як CK – бісектриса, то <ACK=<BCK=α+x.
Тоді <AKC=180-<A-<ACK=180-α-( α+x)=180-2α -x.
Використовуючи теорему про суму суміжних кутів, отримаємо
<AKC=180-<BKC=180-(90-x)90+x.
Прирівнявши отримані вирази при знаходженні <AKC, знайдемо x:
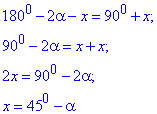
Звідси, отримаємо наступні значення кутів < KCH:
1) 45-8=37 – В,
2) 45-32=13 – Г,
3) 45-28=17 – Д,
4) 45-18=27 – А.
Завдання 30.24 Установити відповідність між катетами a і b (1–4) прямокутних трикутників і значеннями гострого кута, протилежного до катета a (А–Д).

Обчислення: Побудуємо прямокутний трикутник
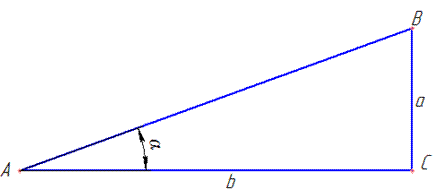
За означенням тангенса гострого кута прямокутного трикутника запишемо:
a/b=tg(α), звідси отримаємо α=arctg(a/b).
Тоді для значень 1 – 4 обчислимо α:
1) 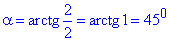 – Б,
– Б,
2) 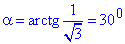 – Д,
– Д,
3) 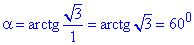 – В,
– В,
4) 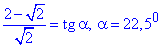 – А.
– А.
Доведення, що останній кут рівний 22,5 градуси слідує з наступної формули половини кута
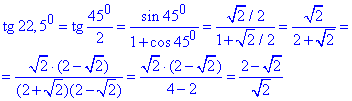 .
.
Завдання 30.25 Установити відповідність між довжинами гіпотенуз і катетів (1–4) прямокутних трикутників і їх площами (А–Д).
1. 5 см, 3 см
2. 13 см, 5 см
3. 10 см, 8 см
4. 25 см, 7 см
А. 84 см2
Б. 6 см2
В. 24 см2
Г. 48 см2
Д. 30 см2
Обчислення: Площа прямокутного трикутника обчислюється за формулою:
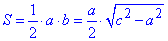
де a і b – катети;
c^2=a^2+b^2 – гіпотенуза прямокутного трикутника.
Виконуємо розрахунки
1) 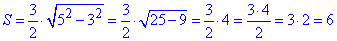 см2 – Б,
см2 – Б,
2) 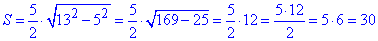 см2 – Д,
см2 – Д,
3) 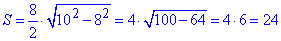 см2 – В,
см2 – В,
4) 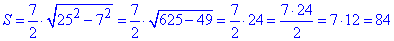 см2 – А.
см2 – А.
В наступних уроках розберемо задачі на рівносторонні, рівнобедрені трикутники та інші фігури, які Ви маєте вивчити на уроках з геометрії.


