Сьогодні маєте можливість разом проаналізувати розв'язки ЗНО тестів на знаходження площі прямокутного трикутника. В наступних статтях підуть задач на рівнобедрені трикутники все що з ними пов'язано. Пізніше цей розділ доповнимо формулами, хоча вони тут містяться на кожному кроці, лише потрібно погортати відповіді до прикладів.
Приклад 30.29 У прямокутному трикутнику висота і медіана, проведені до гіпотенузи, відповідно дорівнюють 24 см і 25 см.
Знайти у сантиметрах периметр трикутника.
Розв'язування: Нехай маємо прямокутний трикутник ABC (∠C=90), у якого CH=24 см – висота і CM=25 см – медіана, що проведені до гіпотенузи AB (за умовою). Виконаємо рисунок трикутника і всього, що задано
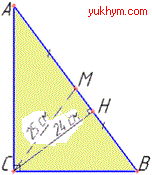
У прямокутному ΔCHM (∠CHM=90), за теоремою Піфагора, знайдемо катет HM:
HM^2=CM^2-CH^2,
HM^2=25^2-24^2,
HM^2=(25-24)(25+24)=1•49=7^2,
HM=7 см.
Нехай AM=x, тоді BM=AM=x (CM - медіана ΔABC).
Звідси слідує AH=AM+HM=x+7 і BH=BM-HM=x-7 – проекції катетів AC, BC, відповідно, на гіпотенузу AB.
За властивістю прямокутного трикутника CH^2=AH•BH (це виводиться із подібності прямокутних трикутників ABC і CBH).
24^2=(x+7)(x-7)=x^2-49,
x^2=576+49=625=25^2,
x=25.
AM=BM=25 см, звідси AB=AM+BM=25+25=50 см – гіпотенуза. AH=25+7=32 см і BH=25-7=18 см.
У прямокутному ΔACH (∠AHC=90), у якого AH=32 см і CH=24 см – катети, за теоремою Піфагора знайдемо гіпотенузу AC:
AC^2=AH^2+CH^2=32^2+24^2=1600=40^2,
звідси AC=40 см.
У прямокутному ΔBCH (∠BHC=90), у якого BH=18 см і CH=24 см – катети, за теоремою Піфагора знайдемо гіпотенузу BC:
BC^2=BH^2+CH^2=18^2+24^2=900=30^2,
звідси BC=30 м.
Знайдемо периметр ΔABC:
PΔABC=AB+AC+BC=50+40+30=120 см.
Відповідь: 120.
Приклад 30.33 Точка дотику вписаного в прямокутний трикутник кола ділить гіпотенузу на відрізки 3 см і 10 см.
Знайти у квадратних сантиметрах площу трикутника.
Розв'язування: Нехай маємо прямокутний трикутник ABC (∠C=90), у якого вписане коло з центром у точці O.
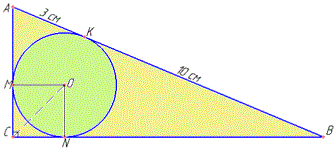
Коло дотикається:
до гіпотенузи AB в точці K, причому AK=3 см і BK=10 см (за умовою);
до катета AC в точці M;
до катета BC в точці N.
За властивістю трикутника і вписаного в нього кола отримаємо:
AM=AK=3 см, BN=BK=10 см і CM=CN (позначимо CM=CN=x).
Звідси отримаємо:
AB=AK+BK=3+10=13 см – гіпотенуза, AC=AM+CM=3+x і BC=BN+CN=10+x – катети прямокутного ΔABC.
У прямокутному ΔABC за теоремою Піфагора запишемо рівність:
AC^2+BC^2=AB^2,
(3+x)^2+(10+x)^2=13^2,
9+6x+x^2+100+20x=x^2=169,
2x^2+26x-60=0,
x^2+13x-30=0,
за теоремою Вієта, отримаємо
x1=2 і x2=-15<0,
звідси AC=3+2=5 см і BC=10+2=12 см - катети прямокутного ΔABC.
Знайдемо площу прямокутного ΔABC:
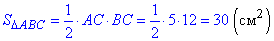
Відповідь: 30.
Приклад 30.36 Бісектриса прямого кута прямокутного трикутника поділяє гіпотенузу на відрізки, що дорівнюють m і n.
Визначити висоту, проведену з вершини прямого кута, площу трикутника й обчислити їх значення, якщо m=3, n=4.
Розв'язування: Нехай маємо прямокутний трикутник ABC (∠C=90), у якого CL – бісектриса, яка проведена до гіпотенузи AB, тоді AL=m і BL=n (за умовою).
Тоді AB=AL+BL=m+n – гіпотенуза прямокутного ΔABC.
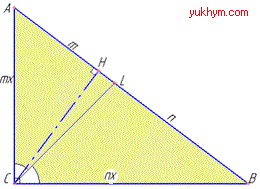
За властивістю бісектриси трикутника (бісектриса поділяє протилежну сторону пропорційно бічним сторонам) запишемо:
AL:BL=AC:BC.
Позначимо AC=mx, тоді BC=nx, де x – коефіцієнт пропорційності.
За теоремою Піфагора запишемо рівність і знайдемо x:
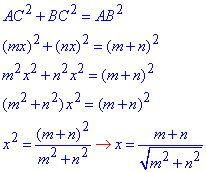
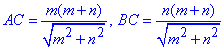– катети прямокутного ΔABC.
Знайдемо площу SΔABC прямокутного ΔABC:
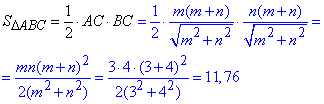
Знайдемо висоту CH прямокутного ΔABC:
SΔABC=AB*CH/2, звідси
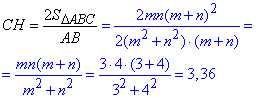
Відповідь: 3,36; 11,76.
Приклад 30.37 У прямокутному трикутнику висота і бісектриса, проведені з вершини прямого кута, відповідно дорівнюють h і l.
Визначити площу трикутника й обчислити її значення, якщо h=0,5, l=0,7.
Розв'язування: Нехай маємо прямокутний трикутник ABC (∠C=90), у якого CL=l – бісектриса і CH=h – висота, які проведені до гіпотенузи AB. 
Нехай ∠A=alpha. У прямокутних трикутників ABC і CBH (∠C=90) кут B спільний, тому такі трикутники подібні, звідси слідує, що ∠BCH=∠A=alpha.
Оскільки ∠C=90, то за означенням бісектриси CL отримаємо:
∠ACL=∠BCL=∠C:2=45.
1) За означенням синуса ∠A=alpha і косинуса ∠BCH=alpha гострих кутів прямокутних трикутників ABC і CBH відповідно, отримаємо
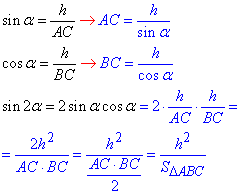
2) За теоремою Піфагора в трикутнику ΔABC (з врахуванням пункту 1) маємо
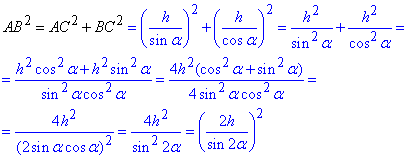
звідси AB=2h/sin(2*alpha).
3) Запишемо теорему синусів для трикутників ACL і BCL відповідно; виразимо довжини відрізків AL, BL і AB=AL+BL:
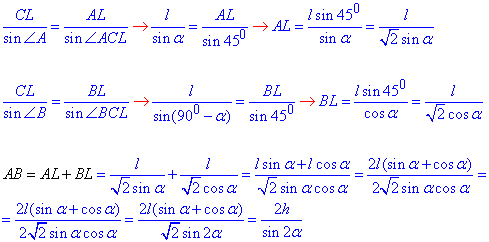
кінцева формула
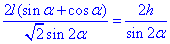
4) З останньої рівності запишемо вираз для sin(2•alpha):
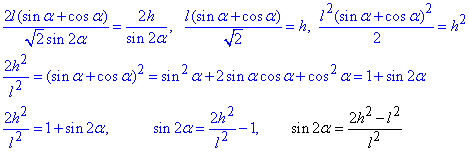
5) З пунктів 1) і 4) прирівняємо вирази для sin(2•alpha)
і знайдемо площу прямокутного трикутника ΔABC:
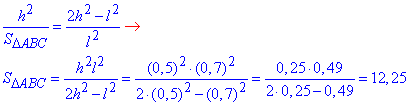
Відповідь: 12,25.
Приклад 30.35 Знайти у квадратних сантиметрах площу прямокутного трикутника, якщо його висота ділить гіпотенузу на відрізки 18 см і 32 см.
Розв'язування: Нехай маємо прямокутний трикутник ABC (∠C=90).
CH=h – висота, яка проведена до гіпотенузи AB і AH=32 см,
BH=18 см – проекції катетів AC, BC на гіпотенузу AB, відповідно (за умовою).
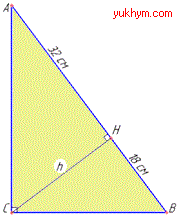
Тоді AB=AH+BH=32+18=50 (см) – гіпотенуза прямокутного ΔABC.
За властивістю прямокутного трикутника h^2=AH•BH, звідси
h^2=AH•BH=18•32=24^2,
CH=h=24 см.
Знайдемо площу прямокутного ΔABC:
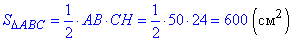
Відповідь: 600 см2.
В наступній статті Вас чекають задачі на знаходження радіуса вписаного та описаного кіл в прямокутному трикутнику.
