Рівнобедрені трикутники. 25 задач на площу, периметр, радіус

На сайті наведені готові відповіді до понад 400 задач з цього посібника, які дозволяють швидко та якісно підготуватися до ЗНО з математики. Далі будуть наведені пояснення до 25 задач на рівнобедрені та рівносторонні трикутники.

Ви можете завантажити без реєстрації відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).

Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж

Зміст: Посібник містить поради щодо проходження ЗНО з математики та подібні до тестових завдання.
Усі задачі однієї теми розміщені в порядку зростання складності.
Рекомендуємо всім завантажити відповіді до ЗНО та самостійно пройти теми, з якими маєте труднощі на практичних.

Тема 31. Рівнобедрені трикутники

Приклад 31.1 Знайти периметр рівнобедреного трикутника зі сторонами 3 см і 7 см.
Обчислення: Завдання одне з найпростіших, але без знання властивостей трикутників відповідь може бути неправильна.
"Чому так буває?"- читайте наступне правило:
Оскільки за теоремою про нерівність трикутника:
«третя сторона трикутника завжди менша за суму двох інших сторін», то довжини бічних сторін заданого рівнобедреного трикутника дорівнюють по 7 см, а основа дорівнює 3 см.
Звідси, маємо
P=7+7+3=17 см.
Виконаємо схематичний рисунок до задачі на основі проведеного вище аналізу
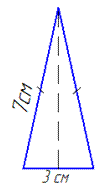А зараз спробуйте самостійно побудувати трикутник в якого основа рівна 7 см, а сторони 3 см.
Що Ви отримаєте в результаті?
Відповідь: 17 см – Г.

Приклад 31.2 У рівнобедреному трикутнику ABC кут C дорівнює 104⁰. Знайти кут B.
Обчислення: Оскільки за умовою задачі ∠C=104⁰, а сума кутів трикутника дорівнює 180⁰, то позначимо через AC і BC – бічні сторони рівнобедреного трикутника, AB – основа.
Схематичний рисунок до задачі матиме вигляд
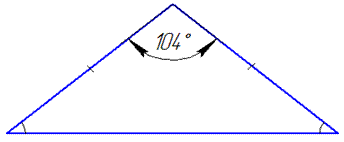За ознакою рівнобедреного трикутника (кути при основі AB рівні) маємо:
∠A=∠B.
Сума внутрішніх кутів рівна ∠A+∠B+∠C=180, звідси 2•∠B+∠C=180 можемо знайти кут ∠B: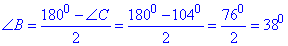

Відповідь: 38⁰ – В.

Приклад 31.3 Знайти площу рівнобедреного трикутника, у якого бічна сторона дорівнює 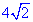см, а кут між бічними сторонами дорівнює 30⁰.
Обчислення: Оскільки у рівнобедреному трикутнику бічні сторони рівні, то 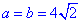см.
Нехай alpha=30 – кут між бічними сторонами.
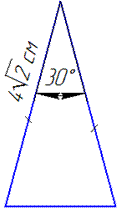Обчислимо площу трикутника за двома сторонами a, b і кутом alpha між ними:

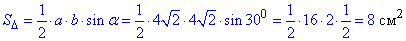
Відповідь: 8 см² – Д.

Приклад 31.4 У рівнобедреному трикутнику бічна сторона дорівнює 10 см, а висота, що проведена до основи, - 6 см. Знайти площу трикутника.
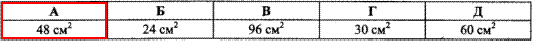Обчислення: У рівнобедреному трикутнику висота проведена до основи, є медіаною і бісектрисою.
Маємо AB=BC=10 см – бічні сторони рівнобедреного ΔABC, BH=6 см – висота, BH⊥AC
За властивістю запишемо:
AH=CH.
У прямокутному трикутнику ABH (∠ABH=90) знайдемо катет AH за теоремою Піфагора:
AH^2=AB^2-BH^2, звідси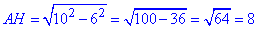
см.
Оскільки BH – медіана трикутника, то AC=2•AH=2•8=16 см.
Обчислимо площу за стороною AC і висотою BH: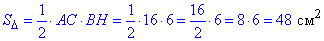

Відповідь: 48 см² – А.

Приклад 31.5 У рівнобедреному трикутнику висота, проведена до бічної сторони, поділяє її на відрізки 8 см і 2 см, починаючи від вершини кута між бічними сторонами. Знайти площу трикутника.
Обчислення: У рівнобедреному ΔABC маємо AD=2 см, BD=8 см, CD перпендикулярна до AB (за умовою).
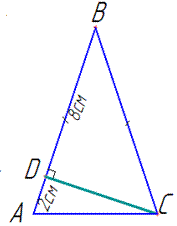рівнобедрений трикутник AB=AD+BD=8+2=10 см, AB=BC=10 см – бічні сторони рівнобедреного ΔABC.
У прямокутному трикутнику BCD (∠BDC=90) знайдемо катет DC:
DC^2=BC^2-BD^2, звідси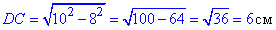

Обчислимо площу трикутника за стороною AB і висотою CD: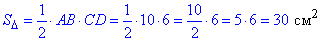

Відповідь: 30 см² – Г.

Приклад 31.6 У рівнобедреному трикутнику основа дорівнює 6 см, а радіус кола, описаного навколо трикутника, - 5 см. Знайти висоту, проведену до основи.

Обчислення: Маємо AC=6 см – основа, AB=BC – бічні сторони рівнобедреного трикутника ABC.
Точка O – центр описаного кола навколо ΔABC.
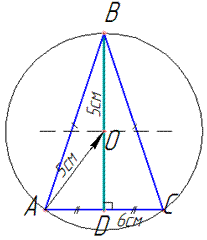Оскільки центр описаного кола лежить на перетині серединних перпендикулярів і медіана, опущена до основи рівнобедреного трикутника, є висотою, то точка O лежить на медіані BD. Звідси, OA=OB=5 см – радіус описаного кола, AD=DC=AC/2=3 см, BD перпендикулярна до AC.
У прямокутному трикутнику (∠ADO=90) знайдемо катет OD:
OD^2=OA^2-AD^2, тобто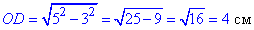

Обчислимо висоту BD, проведену до основи AC.
BD=OB+OD=5+4=9 см.
Відповідь: 9 см – Б.

Приклад 31.7 У рівнобедреному трикутнику кут при основі дорівнює alpha, а радіус кола, вписаного в трикутник, дорівнює r.
Визначити бічну сторону трикутника.
Обчислення: У рівнобедреному трикутнику ABC:
AC – основа, AB=BC – бічні сторони, ∠BAC=alpha, BH – медіана (вона є і висотою, і бісектрисою), тому AH=HC, звідси AC=2AH.
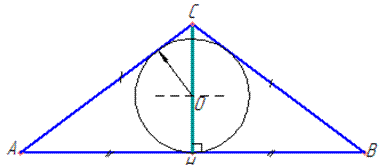Радіус кола, вписаного в трикутник обчислюється за формулою:

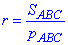
де площа трикутника ABC рівна

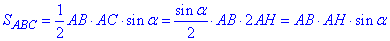
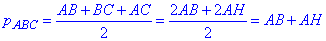– півпериметр трикутника.
Розглянемо прямокутний трикутник:
ΔABH (∠AHB=90), ∠BAC=alpha.
Запишемо сторону AH:

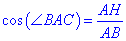
звідси отримаємо AH=AB•cos(alpha).
Підставимо отримані вирази у формулу для обчислення r і знайдемо AB.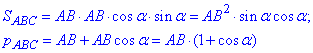

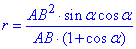
звідси отримаємо

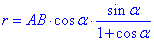
і отже,

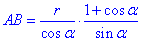
Враховуючи, що запис містить формулу половини котангенса

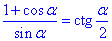
остаточно отримаємо залежність

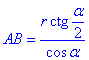
Відповідь: – Д.

Приклад 31.8 Знайти площу рівностороннього трикутника зі стороною 2√3 см.
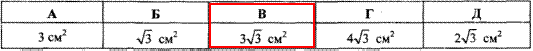Обчислення: Оскільки у рівностороннього трикутника всі кути (і сторони) рівні, то внутрішні кути рівні 60 градусів

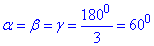
a=b=c - сторони рівностороннього трикутника.

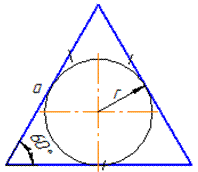
Обчислимо площу трикутника за двома сторонами та кутом між ними: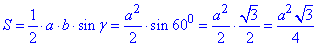

Отримали формулу для обчислення площі рівностороннього трикутника.
Підставимо значення сторони та знайдемо площу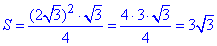

Відповідь: 3√3 см² - В.

Приклад 31.9 Радіус кола, вписаного в рівносторонній трикутник, дорівнює 4√3 см. Знайти сторону трикутника.

Обчислення: Обчислимо півпериметр рівностороннього трикутника:
p=P/2=3a/2.

Враховуючи міркування попередніх двох задач, отримаємо

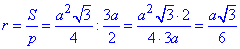
Отримали формулу для обчислення радіуса кола, вписаного в рівносторонній трикутник.
Виразимо сторни через радіус вписаного кола

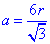
Підставимо у формулу r=4√3 см і знайдемо сторону рівностороннього трикутника:

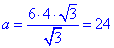
Відповідь: 24 см - В.

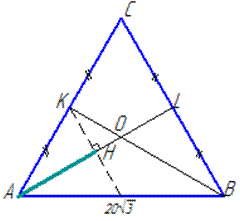
Приклад 31.10 Сторона правильного трикутника дорівнює 20√3 см.
Знайти проекцію однієї медіани на іншу.
Обчислення: У рівностороннього трикутника будь-яка медіана є висотою і бісектрисою.
Тому обчислимо висоту правильного трикутника (зі стороною a) через площу:
S=a•ha/2, звідси

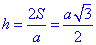
де 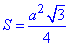– площа трикутника.
На основі формули знаходимо
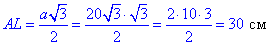– довжина медіани правильного трикутника.

З точки K опустимо перпендикуляр KH до медіани AL, тоді AH – проекція медіани BK на медіану AL.
Обчислимо довжину AH.
Оскільки сторони перпендикулярні KH⊥AL, BC⊥AL, то за теоремою KH||CL.
Розглянемо прямокутні трикутники AKH (∠AHK=90) і ACL (∠ALC=90).
У них ∠A спільний, тому за теоремою трикутники AKH, ACL - подібні.
Оскільки BK - медіана, то AK=AC/2, звідси AH=AL/2, бо у подібних трикутників сторони пропорційні, отже AH=AL/2=30/2=15 см.
Відповідь: 15 см – А.

Приклад 31.11 У рівнобедреному трикутнику бісектриси кутів при основі утворюють при перетині кут 52 градуси.
Знайти кут між бічними сторонами трикутника.
Обчислення: У ΔABC маємо AL і CK – бісектриси кутів A і C, відповідно.
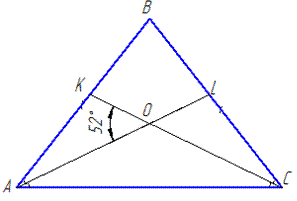Тоді ∠OAK= ∠OAC, ∠OCL= ∠OCA.
Оскільки ΔABC – рівнобедрений за умовою, то ∠A= ∠C (як кути при основі AC).
Звідси, ∠OAC= ∠OCA.
∠AOC суміжний з кутом градуси за умовою), тоді ∠AOC+ ∠AOK=180, звідси ∠AOC=180- ∠AOK=180-52=128.
Розглянемо ΔAOC, у якого ∠AOC=128 і ∠OAC= ∠OCA.
За теоремою про суму кутів трикутника маємо:
∠AOC+ ∠OAC+ ∠OCA=180,
128=2• ∠OAC=180, звідси

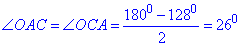
За означенням бісектриси в ΔABC маємо:
∠A= ∠C=2• ∠OCA=2•26=52.
У ΔABC за теоремою про суму кутів трикутника знайдемо ∠B – кут між бічними сторонами рівнобедреного трикутника:
∠A+ ∠B+ ∠C=180,
2• ∠A+ ∠B=180,
∠B=180-2•52=76.
Відповідь: 76⁰ – В.

Приклад 31.12 O – точка перетину висот AM і CK рівнобедреного трикутника ABC з основою AC.
Знайти кут B, якщо ∠AOC=110.
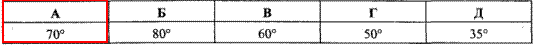Обчислення: У ΔABC відомо, що AM і CK – висоти, проведені до сторін BC і AB, відповідно.
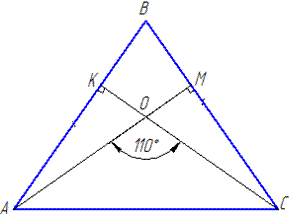Тоді ∠AKC= ∠AMC=90. суміжний з кутом за умовою), тоді ∠AOC+ ∠AOK=180, звідси ∠AOK=180-∠AOC=180-110=70.
Розглянемо ΔAOK, у якого ∠AOK=70 і ∠AKO=90.
За теоремою про суму кутів трикутника маємо:
∠AOK+∠OAK+∠OKA=180,
∠OAC=180-90-70=20, звідси ∠OAK=∠OAB=20.
Розглянемо ΔABM, у якого BAM=20 і ∠AMB=90.
За теоремою про суму кутів трикутника маємо:
∠AMB+∠BAM+∠ABM=180,
∠ABM=180-90-20=70, звідси ∠B=∠ABM=70.
Відповідь: 70⁰ – А.