Продовжуємо розбирати пояснення до 25 задач на рівнобедрені та рівносторонні трикутники.
Ви можете завантажити без реєстрації відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Зміст: Посібник містить поради щодо проходження ЗНО з математики та подібні до тестових завдання.
Усі задачі однієї теми розміщені в порядку зростання складності.
Рекомендуємо всім завантажити відповіді до ЗНО та самостійно пройти теми, з якими маєте труднощі на практичних.
Тема 31. Рівнобедрені трикутники
Приклад 31.13 Бічна сторона рівнобедреного трикутника дорівнює 55 см, а висота, що проведена до основи - 44 см.
Знайти відношення відрізків, на які поділяє бічну сторону бісектриса кута при основі.
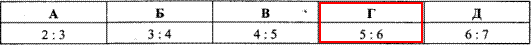Обчислення: У рівнобедреному ΔABC відомо:
AB=BС=55 см і BР=44 см (BH⊥AC).
BK і KA – відрізки, на які поділяє бічну сторону AB бісектриса CK.
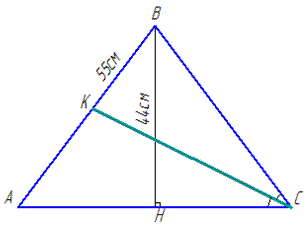За властивістю медіани AH=HC=AC/2, з цього слідує, що AC=2•AH.
У прямокутному ΔABH (∠AHB=90) за т. Піфагора знайдемо катет AH:
AH^2+BH^2=AB^2, звідси
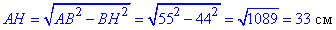
Тому AC=2•AH=2•33=66 см – основа рівнобедреного ΔABC.
Оскільки, за властивістю, бісектриса трикутника ділить протилежну сторону пропорційно до бічних сторін, то маємо BK/KA=BC/AC.
Звідси отримаємо шукану пропорцію
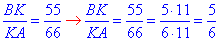
або запис вигляду BK:KA=5:6.
Відповідь: 5:6 – Г.
Приклад 31.14 Сторона рівностороннього трикутника дорівнює 8√3 см.
Знайти радіус кола, яке проходить через середини сторін трикутника.
Обчислення: Оскільки у рівносторонньому трикутнику кожна медіана проведена до будь-якої сторони є висотою і бісектрисою (за властивістю), то коло, яке проходить через середини сторін правильного трикутника, є вписаним у цей трикутник.
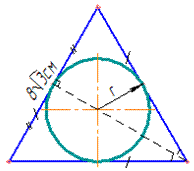Звідси записуємо a=8√3 см – сторона рівностороннього трикутника;
p=P/2=3a/2=12√3 см – півпериметр рівностороннього трикутника;
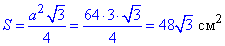– площа рівностороннього трикутника;
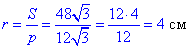– радіус вписаного в правильний трикутник кола.
(Усі попередні три формули виведені в задачах 31.8, 31.9).
Відповідь: 4 см – В.
Приклад 31.15 Знайти радіус кола, вписаного в рівнобедрений трикутник, основа якого дорівнює 160 см, а висота, проведена до неї, - 60 см.
Обчислення: У рівнобедреному ΔABC маємо:
AB=BC, AC=160 см і BK=60 см (BK⊥AC), де AB і BC – бічні сторони, AC – основа і BK – висота рівнобедреного ΔABC.
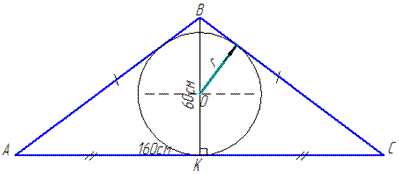За властивістю медіани, яка проведена до основи у рівнобедреному трикутнику (це висота і бісектриса), маємо AK=KC=AC/2=160/2=80 см.
У прямокутному трикутнику ABK (∠AKB=90) знайдемо AB:
AK^2+BK^2=AB^2, звідси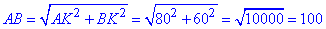 
см.
Знайдемо півпериметр p і площу S рівнобедреного трикутника ABC:
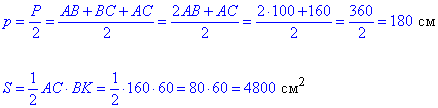
Обчислимо радіус r кола, вписаного в рівнобедрений трикутник ABC:
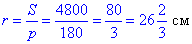
Відповідь: 26 і 2/3см – А.
Приклад 31.16 Знайти відстань від точки перетину медіан до центра кола, вписаного в рівнобедрений трикутник з основою 160 см і бічною стороною 100 см.
Обчислення: У рівнобедреному ΔABC маємо:
AB=BC=100 см, AC=160 см, де AB і BC – бічні сторони,
AC – основа рівнобедреного ΔABC;
BK і CM – медіани рівнобедреного ΔABC проведені до AC і AB, відповідно.
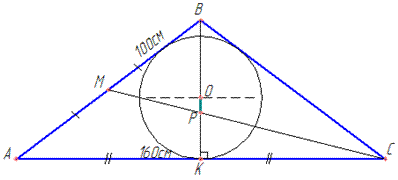За властивістю - медіана, яка проведена до основи у рівнобедреному трикутнику є висотою і бісектрисою.
Звідси, AK=KC=AC/2=160/2=80 см.
У прямокутному трикутнику ABK ( ∠AKB=90) знайдемо BK:
AK^2+BK^2=AB^2, звідси медіана рівна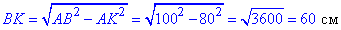
Медіани у будь-якому трикутнику в точці перетину діляться у відношенні 2:1, починаючи від вершини.
Отже, BP:PK=2:1, де P – точка перетину медіан.
Нехай, PK=x, тоді BP=2x, BP+PK=BK=60 см, звідси 2x+x=60, x=20, PK=20 см.
Знайдемо півпериметр p і площу S рівнобедреного трикутника ABC:
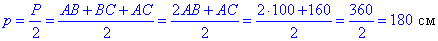
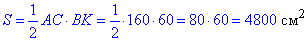
Обчислимо радіус r кола, вписаного в рівнобедрений трикутник ABC:
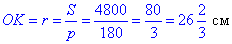
Знайдемо довжину відрізка OP – відстань від точки перетину медіан до центра кола.
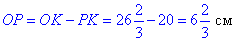
Відповідь: 6 і 2/3 см – Г.
Приклад 31.17 Центр кола, вписаного в рівнобедрений трикутник, поділяє висоту, що проведена до основи, у відношенні 10:3.
Знайти периметр трикутника, якщо бічна сторона дорівнює 20 см.
Обчислення: У рівнобедреному ΔABC задано:
AB=BC=20 см, де AB і BC – бічні сторони,
AC – основа і BH – висота рівнобедреного трикутника.
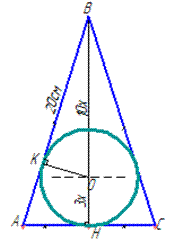пригадуємо, що медіана у рівнобедреному трикутнику є бісектрисою та висотою.
Звідси, AH=HC=AC/2, тому AC=2•AH.
Нехай, BO=10x, OH=3x – відрізки, на які поділяє висоту BH центр кола O, вписаного в рівнобедрений трикутник ABC.
Тут OK=OH=3x – радіус вписаного кола, тому OK⊥AB (радіус перпендикулярний до дотичної, тобто до сторони).
Розглянемо прямокутні трикутники ABH (∠AHB=90) і OBK (∠OKB=90).
В них ∠ABH= ∠OBK – спільний кут, тому трикутники ABH, OBK подібні за ознакою подібності прямокутних трикутників.
Звідси отримуємо пропорцію
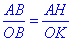
Підставимо відомі значення сторін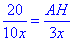
Звідси половина основи рівна
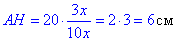
Довжина основи AC=2•AH=2•6=12 см.
Обчислимо периметр рівнобедреного трикутника:
P=AB+BC+AC=2AB+AC=2•20+12=52 см.
Відповідь: 52 см – Д.
Приклад 31.18 Основа і бічна сторона рівнобедреного трикутника відповідно дорівнюють 16 см і 10 см.
Знайти висоту трикутника, проведену до бічної сторони.
Обчислення: У рівнобедреному ΔABC відомо:
AB=BC=10 см, AC=16 см, BK⊥AC, де AB і BC – бічні сторони, AC – основа і BK – висота рівнобедреного ΔABC.
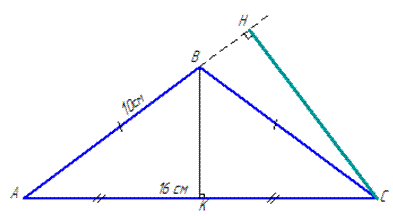За властивістю медіани, яка проведена до основи у рівнобедреному трикутнику (це висота і бісектриса), маємо AK=KC=AC/2=16/2=8 см.
У прямокутному трикутнику ABK (∠AKB=90) знайдемо катет BK:
AK^2+BK^2=AB^2, звідси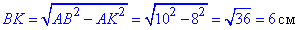 
Знайдемо площу ΔABC:
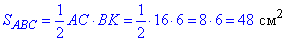
Знайдемо висоту CH, яка проведена до бічної сторони AB (CH⊥AB):
На основі формули площі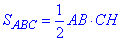
знаходимо залежність для обчислення висоти
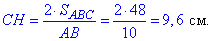
Відповідь: 9,6 см – Г.
Приклад 31.19 Бічна сторона рівнобедреного трикутника дорівнює 48 см.
За якого значення висоти, проведеної до основи, площа трикутника буде найбільшою?
Обчислення: У рівнобедреному ΔABC маємо:
AB=BC=48 см, BH⊥AC, де AB і BC – бічні сторони,
AC – основа і BH – висота рівнобедреного трикутника.
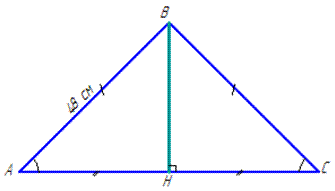За властивістю медіани, яка проведена до основи у рівнобедреному трикутнику (це висота і бісектриса), маємо AH=HC=AC/2, звідси AC=2•AH.
Медіана, що проведена до основи рівнобедреного трикутника розбиває його на два рівних прямокутних трикутники (ознака рівності трикутників за трьома сторонами). Тому найбільша площа рівнобедреного трикутника буде, якщо буде найбільша площа кожного прямокутного трикутника, з якого складається рівнобедрений трикутник.
Найбільша площа прямокутний трикутник буде мати у випадку, коли катети будуть рівні (це твердження і розв'язок цієї задачі взагалі доводять за допомогою похідної).
Тобто у прямокутному трикутнику ABH (∠AHB=90) площа приймає максимальне значення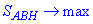 
якщо AH=BH.
За теоремою Піфагора маємо:
AB^2=AH^2+BH^2, AB^2=2•BH^2, звідси
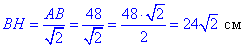
Отже, для того щоб площа заданого рівнобедреного трикутника була найбільшою необхідно щоб висота, що проведена до основи ΔABC була рівна:
BH=24√2 см.
Відповідь: 24√2 см – Б.
Сподіваємося наведені готові відповіді до задач на трикутники будуть для Вас корисними у навчанні та при підготовці до ЗНО.
Залишилося розібрати ще 6 прикладів, які передбачають до 4 підпунктів у кожному завданні на визначення площі, сторін трикутника, радіусів вписаних кіл.
