Задачі, які починаються зі слів "висота проведена з прямого кута" або "висота прямокутного трикутника ділить гіпотенузу" на відрізки (у відношенні) досить популярні в шкільному курсі.
У відповіді потрібно знайти висоту, площу або периметр прямокутного трикутника.
Багато школярів справляються із завданням на "5", інші не розуміють як за нього братися.Хід усіх завдань ґрунтується на двох дуже важливих властивостях про пропорційні відрізки у прямокутному трикутнику.
Щоб їх краще пояснити, розглянемо прямокутний трикутник ABC.
З вершини С до гіпотенузи проведена висота, яка ділить її на відрізки BD і AD.
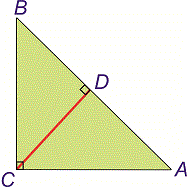
Властивість 1. Висота прямокутного трикутника рівна проекції катетів на гіпотенузу.
Мовою формул, твердження еквівалентне запису
СD*СD=АD∙DВ
Властивість 2. Катет прямокутного трикутника є середнім пропорційним гіпотенузі і проекції цього катета на гіпотенузу
AC*AC=AB*AD;
BC*BC=AB*BD.
Добре розберіться, за що відповідають формули –наведені далі задачі будуть для Вас більш зрозумілі.
Задача 1. Висота прямокутного трикутника ділить гіпотенузу на два відрізки 4 см і 9 см. Знайдіть висоту трикутника, проведену до гіпотенузи та його площу.
Розв'язання: Виконаємо побудову трикутника за даними
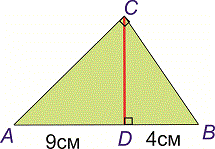
За 1 властивістю висота рівна
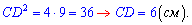
Гіпотенузу знаходимо через суму відрізків
AB=AD+BD=4+9=13 (см).
Площа трикутника рівна половині добутку основи на висоту. Виконуємо обчислення
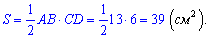
Відповідь: Площа рівна 39 сантиметрів квадратних.
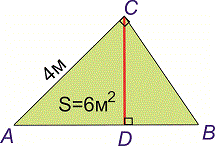
Задача 2. Площа прямокутного трикутника рівна 6 метрів квадратних. Знайти проекції катетів на гіпотенузу, якщо відомо, що один катет рівний 4 м.
Розв'язання: Виконаємо допоміжну побудову трикутника
Через відому площу обчислимо другий катет трикутника
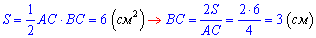
За теоремою Піфагора знаходимо гіпотенузу
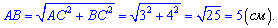
Через пропорційні відрізки знаходимо проекції
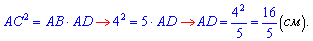
В такий самий спосіб знаходимо проекцію другого катета
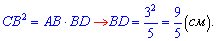
Легко переконатися, що сума проекцій рівна гіпотенузі трикутника
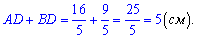
Відповідь: проекції катетів рівні 9/5 см та 16/5 см.
Задача 3. Один катет прямокутного трикутника рівний 8 см, а проекція другого катета на гіпотенузу – 3,6 см. Знайдіть другий катет та гіпотенузу трикутника.
Розв'язання: Зобразимо трикутник із вхідними даними.
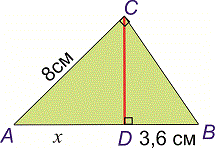
Позначимо AD=x. Згідно другої властивості маємо
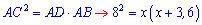
Розкриваємо дужки
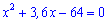
Квадратне рівняння обчислюємо через дискримінант
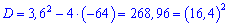
Корені рівняння рівні
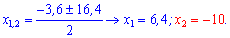
Корінь x=-10 не відповідає фізичній суті задачі.
Знаючи другу проекцію AD=6,4 см гіпотенузу знаходимо через суму проекцій
AB=3,6+6,4=10 (см.)
За теоремою Піфагора обчислюємо другий катет
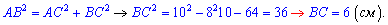
Відповідь: катетів рівний 6 см, гіпотенуза – 10 см.
Подібних задач на висоту, гіпотенузу, бісектрису трикутника в інтернеті багато, важчі з них залишайте у коментарях і ми їх розв'яжемо для Вас.


