Перетворення подібності вивчають в 9, 10 класі на уроках геометрії на прикладі точок та прямих.
Сьогодні почнемо розбирати групу завдань із ЗНО підготовки на геометричні перетворення. Готові розв'язки розділені на 6 уроків, спершу йде симетрія та ескіз точок, далі паралельне перенесення прямих, парабол, кіл. Обчислення центра та коефіцієнта гомотетії. Теорію Ви повинні знати, якщо в ній "плаваєте" то спершу перечитайте відкриту в онлайн доступі статтю на "Геометричні перетворення. Перетворення подібності". Головні правила, означення, теореми та формули виділені в поясненнях , тому на них просимо звернути увагу та вивчати.
Тема: Перетворення фігур
Приклад 43.2 Знайти координати точки, симетричної точці (3;5) відносно початку координат.
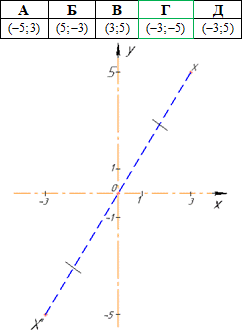
Розв'язування: Дві точки X та X’ називають симетричними відносно даної точки O, якщо точка O – середина відрізка XX’.
Точку O вважають симетричною самій собі й називають центром симетрії.
Маємо точку X(3;5) і центр симетрії O(0;0) (початок координат).
За означенням точка O – середина відрізка XX’ (XO=OX’), тому знайдемо координати точки x(x;y):
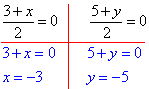
Отримали X’(-3;-5).
На майбутнє Ви повинні знати, якщо точка O(0;0) (початок координат) є центром симетрії деяких інших точок, то їх відповідні координати мають лише протилежні знаки.
Відповідь: (-3;-5) – Г.
Приклад 43.4 Знайти координати точки, симетричної точці (-3;4) відносно осі Ox.
Розв'язування: Дві точки X та X’ називають симетричними відносно прямої l, якщо пряма l є серединним перпендикуляром до відрізка XX’.
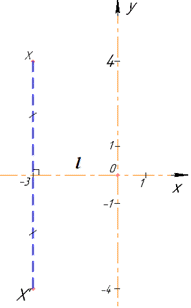
Маємо точку X(-3;4) і пряму, яка є віссю Ox. За означенням вісь Ox – серединний перпендикуляр до відрізка XX’, тому відрізок перпендикулярний до осі абсцис XX’⊥Ox і перпендикулярний до осі ординат XX’||Oy. Це означає, що точка (-3;0) – середина відрізка XX’, а точка X’ має координати (-3;-4).
Взагалі кажучи, точки, симетричні відносно осі ординат Ox, мають однакові абсциси та протилежні ординати.
Відповідь: (-3;-4) – Г.
Приклад 43.8 При паралельному перенесенні точка A(2;3) переходить у точку A’(5;1). У яку точку перейде при цьому паралельному перенесенні точка B(-2;1)?
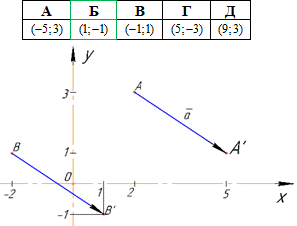
Розв'язування: Уважно розберіть алгоритм обчислень для заданого типу завдань.
Знайдемо координати вектора 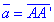 , при якому здійснюється паралельне перенесення з точки A(2;3) в точку A’(5;1):
, при якому здійснюється паралельне перенесення з точки A(2;3) в точку A’(5;1):
ax=xA’-xA=5-2=3;
ay=yA’-yA=1-3=-2.
Звідси a(3;-2).
Знайдемо координати точки B’(x;y), у яку переходить точка B(-2;1) при паралельному перенесенні на вектор a(3;-2):
x=xB+ax=-2+3=1;
y=yB+ay=1-2=-1.
Отже, B’(1;-1).
Відповідь: (1;-1) – Б.
Приклад 43.9 Точка A’(-8;12) – образ точки A(x;-3) при гомотетії з центром у початку координат. Знайти x.
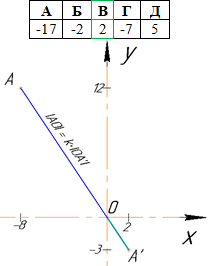
Розв'язування: Гомотетія є перетворенням подібності. На координатній площині гомотетія з центром у початку координат задається формулами:
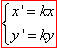
де (x;y) – координати точки A,
а (x’;y’) – координати образу цієї точки при гомотетії.
За умовою маємо точку A(x;-3) і образ A’(-8;12) цієї точки при гомотетії з центром у початку координат, звідси
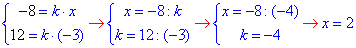
Отримали точку A(2;-3).
На рисунку |AO|=k•|OA’| і при від'ємному коефіцієнті гомотетії k<0 точки A(2;-3) і A’(-8;12) лежать по різні боки від центра гомотетії (точки O(0;0)).
Відповідь: 2 – В.
Приклад 43.19 Точка A(2;-3) – образ точки B(8;6) при гомотетії з центром у точці M(4;0). Знайти коефіцієнт гомотетії.
А | Б | В | Г | Д |
3 | 2 | 0,5 | -2 | -0,5 |
Розв'язування: За умовою точка A(2;-3) – образ точки B(8;6) при гомотетії з центром у точці M(4;0), тоді
|AM|=|k|•|MB|, де k – коефіцієнт гомотетії.
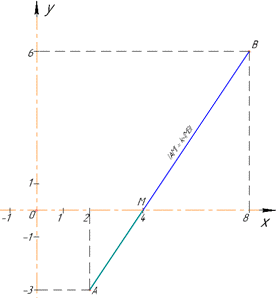
Знайдемо довжину відрізка AM – відстань між точками A(2;3) і M(4;0):
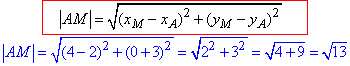
Знайдемо довжину відрізка MB – відстань між точками M(4;0) і B(8;6):
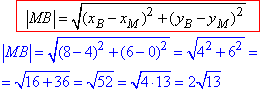
Знайдемо коефіцієнт гомотетії k:
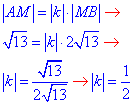
або |k|=0,5.
Оскільки точки A(2;-3) і B(8;6) лежать по різні боки від центру гомотетії (точки M(4;0)), то k<0, звідси k=-0,5.
Відповідь: -0,5 – Д.
Приклад 43.20 Точка M(6;-3) – образ точки N(2;1) при гомотетії з коефіцієнтом k=-1/3. Знайти координати центра гомотетії.
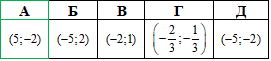
Розв'язування: За умовою точка M(6;-3) – образ точки N(2;1) при гомотетії з коефіцієнтом k=-1/3, тоді
|KM|=|k|•|KN|, де K – координати центра гомотетії.
Гомотетія є перетворенням подібності, це означає, що точки N(2;1), K(x,y) і M(6;-3) лежать на одній прямій.
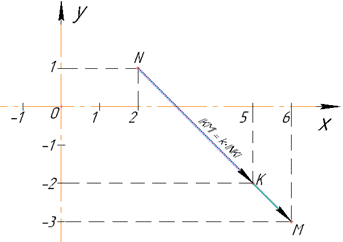
Оскільки k=-1/3, то точки M(6;-3) і N(2;1) лежать по різні боки від центра гомотетії (точки K(x,y)).
Так як |KM|=|-1/3||KN|,
|NM|=|NK|+|KM|,
то |NK|=3|KM| і |NM|=4|KM|.
Нехай маємо вектори NM, NK і KM.
Оскільки точки N(2;1), K(x,y) і M(6;-3) лежать на одній прямій, то NM=NK+KM.
Знайдемо координати вектора NM:
NM=(6-2;-3-1)=(4;-4).
Із умови |NM|=4|KM| знайдемо координати вектора KM:
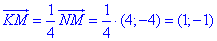
Знайдемо координати точки K(xK;yK) – центра гомотетії:
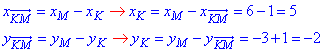
де 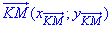 – координати вектора KM і M(xM;yM) – координати точки M.
– координати вектора KM і M(xM;yM) – координати точки M.
Отримали K(5;-2) – центр заданої гомотетії з коефіцієнтом k=-1/3.
Відповідь: (5;-2) – А.
Приклад 43.21 Дано точку A(5;-2). Установити відповідність між перетвореннями (1–4) та координатами образу точки (А–Д).
1. Паралельне перенесення на вектор (3;4) | А. (5;2) |
Розв'язування: 1. Знайдемо координати точки A1(x;y), у яку переходить точка A(5;-2) при паралельному перенесенні на вектор a(3;4):
x=xA+ax=5+3=8,
y=yA+ay=-2+4=2.
Отримали A1(8;2). Д.
2. Якщо точка O(0;0) (початок координат) є центром симетрії деяких інших точок, то їх відповідні координати мають лише протилежні знаки, тому точка A2(-5;2) є образом точки A(5;-2) при симетрії відносно початку координат В.
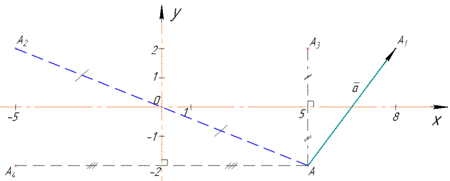
3. Точки, симетричні відносно осі абсцис Ox, мають однакові абсциси та протилежні ординати, тому точка A3(5;2) є образом точки A(5;-2) при симетрії відносно осі Ox. А.
4. Точки, симетричні відносно осі ординат Oy, мають однакові ординати та протилежні абсциси, тому точка A4(-5;-2) є образом точки A(5;-2) при симетрії відносно осі Oy. Г.
Приклад 43.24 Дано точку A(4;6). Установити відповідність між гомотетіями (1–4) та координатами образу точки (А–Д).
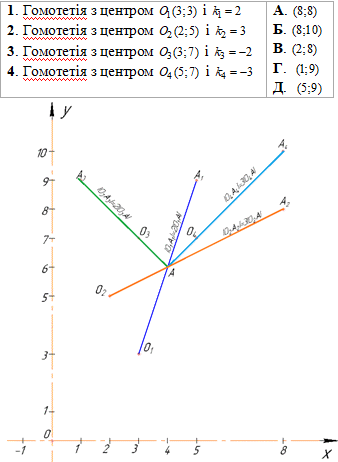
Розв'язування: Гомотетія є перетворенням подібності. На координатній площині гомотетія з центром у початку координат задається формулами:
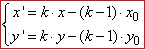
де (x;y) – координати точки A,
k – коефіцієнт гомотетії та
An(x';y') – координати образу цієї точки при гомотетії,
On(x0;y0) – координати центра гомотетії.
Знайдемо координати точок An(x';y') образів при кожній гомотетії.
1. A(4;6), гомотетія з центром O1(3;3) і k1=2:
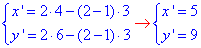
звідси A1(5;9).
На рисунку |O1A1|=2|O1A| і при додатному коефіцієнті гомотетії k>0 точки A(4;6) і A1(5;9) лежать по один бік від центра гомотетії (точки O1(3;3)). Д.
2. A(4;6), гомотетія з центром O2(2;5) і k2=3:
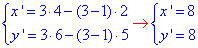
звідси A2(8;8).
На рисунку |O2A2|=3•|O2A| і при k>0 точки A(4;6) та A2(8;8) лежать по один бік від центра гомотетії (точки O2(2;5)). А.
3. A(4;6), гомотетія з центром O3(3;7) і k3=-2:
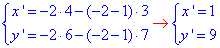
звідси A3(1;9).
На рисунку |O3A3|=2•|O3A| і при від'ємному коефіцієнті гомотетії k<0 точки A(4;6) і A3(1;9) лежать по різні боки від центра гомотетії (точки O3(3;7)). Г.
4. A(4;6), гомотетія з центром O4(5;7) і k4=-3:
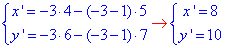
звідси A4(8;10).
На рисунку |O4A4|=3•|O4A| і при k<0 точки A(4;6) і A4(8;10) лежать по різні боки від центра гомотетії (точки O4(5;7)). Б.
Формулу з довільними координатами (x0;y0) центра гомотетії отримали з формули {x'=k•x; y'=k•y} з центром гомотетії у початку координат O(0;0) за допомогою паралельного перенесення точок (x;y) і (x';y') на вектор a(x0;y0), тобто
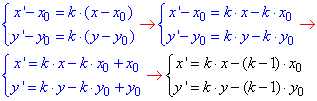
Далі розберемо готові приклади на знаходження координат при повороті точки за та проти годинникової стрілки на заданий кут, та решту розв'язків із ЗНО підготовки на геометричні перетворення.


