Задачі на кути трикутника не важкі, якщо мова йде про 8, 9 клас школи. Але коли йде мова про медіани, бісектриси чи певні побудови то знаходження кутів в трикутнику не таке просте, як може здатися з умов. Далі наведені завдання складнішого типу, вони цікавіші, а їх аналіз точно Вас чогось навчить.
Приклад 30.26 Бісектриса гострого кута прямокутного трикутника утворює з протилежною стороною кути, один з яких дорівнює 70 градусів.
Знайти у градусах менший гострий кут трикутника.
Розв'язування: Нехай маємо прямокутний трикутник ABC (∠C=90), AL – бісектриса, яка проведена до сторони BC, тоді ∠ALC=70 градусів (за умовою).
Побудуємо рисунок трикутника та бісектриси в ньому
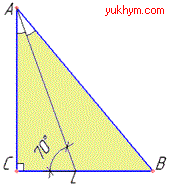
У прямокутному ΔALC (∠ACL=90), за теоремою про суму кутів трикутника, знайдемо ∠CAL:
∠CAL=180-∠ACL-∠ALC=180-90-70=20.
За означенням бісектриси AL в трикутнику ΔABC отримаємо:
∠A=2•∠CAL=2•20=40.
У прямокутному ΔABC (∠C=90), за теоремою про суму кутів трикутника, знайдемо ∠B:
∠B=180-∠C-∠A =180-90-40=50
Отже, ∠A=40 – менший гострий кут ΔABC.
Відповідь: 40 градусів.
Приклади на кути трикутника, та й загалом на геометричні фігури слід розв'язувати з побудови допоміжного рисунку (неважна якість, головне намалювати та позначити задані величини); далі виписування, що задано та самого обчислення шуканих величин.
Як тільки навчитеся будувати геометрію, все решта прийде в процесі розв'язування.
Задача 1. Бісектриса найменшого з кутів прямокутного трикутника утворює з протилежною стороною гострий кут 78 градусів. Знайдіть кути цього трикутника.
Розв'язання: Побудуємо прямокутний трикутник ABC так, що бісектриса кута ∠A перетинає сторону BC в точці F.
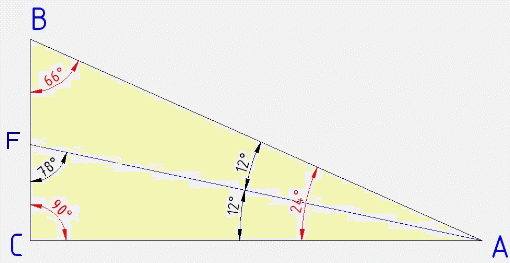
За умовою ∠CFA=78°.
∠CAF=90°-78°=12° - половина гострого кута ∠A.
Оскільки AF - биссектриса, то
∠A=2*∠CAF=2*12°=24°.
Тоді другий гострий кут ΔABC:
∠В=90°-24°=66°.
Відповідь: 24, 66 градусів.
Приклад 31.26 Кут при основі AB рівнобедреного трикутника дорівнює 30 градусів. Висоти трикутника, проведені до бічних сторін, перетинаються в точці O. Знайти у градусах величину кута AOB.
Розв'язування: Нехай маємо рівнобедрений трикутник ABC (AC=BC), у якого ∠BAC=∠ABC=30 – кути при основі AB; BK і AM - висоти, що проведені до бічних сторін AC і BC відповідно, які перетинаються в точці O (за умовою).
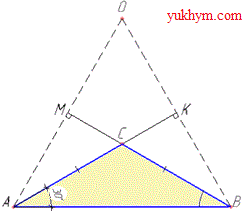
Із прямокутних трикутників AKB (∠AKB=90), AMB (∠AMB=90) знайдемо ∠ABK (причому ∠ABK=∠ABO) і ∠BAM (причому ∠BAM=∠BAO), відповідно (за теоремою про суму кутів трикутника):
,
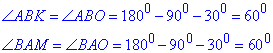У трикутника ABO маємо два рівні кути ∠ABO=∠BAO=60, звідси слідує (за теоремою про суму кутів трикутника), що
∠AOB=180-60-60=60 градусів.
Відповідь: 60.
Приклад 31.34 Знайти у градусах кут між бічними сторонами рівнобедреного трикутника, якщо бісектриса кута при основі відтинає від нього трикутник подібний даному.
Розв'язування: Нехай маємо рівнобедрений трикутник ABC, у якого AC=BC - бічні сторони (∠C - кут між бічними сторонами), AB - основа і AK - бісектриса кута при основі (∠CAK=∠BAK), яка відтинає ΔKBA подібний ΔABC (за умовою).
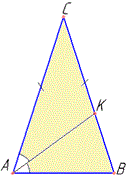Отже, ΔABC~ΔKBA. За властивістю: у подібних трикутників відповідні кути рівні.
Позначимо:∠CAK=∠BAK=alpha, тоді ∠A=∠CAK+∠BAK=2alpha, ∠A=∠B=2alpha (кути при основі AB рівні за властивістю рівнобедреного ΔABC).
Тоді ∠AKB=∠A=2alpha і ∠C=∠BAK=alpha - як відповідні кути.
Отож, у ΔABC отримали: ∠A=∠B=2alpha і ∠C =alpha.
За теоремою про суму кутів трикутника маємо:
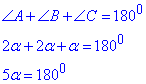
alpha=∠C=36 - кут між бічними сторонами ΔABC.
Відповідь: 36.
Задача 39.25 Величини кутів в трикутнику ABC при вершинах A, B і C відносяться, як 5:6:7.
Знайти величину кута між висотою CD і бісектрисою кута A трикутника.
Розв'язання: Побудуємо заданий трикутник ABC.
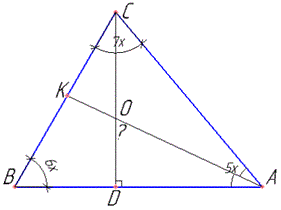
Позначимо його кути:
∠A=5x, ∠B=6x і ∠C=7x, де x - коефіцієнт пропорційності.
За теоремою про суму кутів трикутника маємо:
∠A+∠B+∠C=180, звідси складаємо рівняння
5x+6x+7x=180,
18x=180, x=10.
Отже, отримали ∠A=50, ∠B=60, ∠C=70.
У трикутнику ABC проведемо висоту CD (∠CDA=90) і бісектрису AK кута A (∠BAK=∠CAK=∠A/2=25).
Розглянемо трикутник AOD, у якого ∠ODA=90, ∠OAD=25, а ∠AOD - кут між висотою CD і бісектрисою AK кута A.
За теоремою про суму кутів ΔAOD знайдемо ∠AOD:
∠AOD =180-∠ODA-∠OAD=180-90-25=65.
На цьому всі обчислення до завдання. Уважно перегляньте хід міркувань.
Відповідь: 650.
Задача 39.28 У трикутнику ABC проведено медіану AK, яка дорівнює 13√2/4 й утворює зі стороною AC кут 300.
Знайти BC, якщо ∠BCA=45.
Розв'язання: Розглянемо трикутник AKC, у якого AK=13√2/4, ∠KCA=45 і ∠CAK=30 (за умовою).
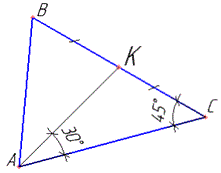
За теоремою синусів знайдемо сторону CK:
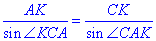
звідси
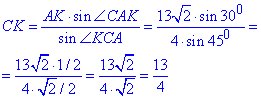
У трикутнику ABC відрізок AK - медіана (за умовою), тому сторона вдвічі більша за знайдений відрізок
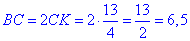
Відповідь: 6,5.
Задача 39.34 Відношення двох внутрішніх кутів трикутника дорівнює 2:3, а зовнішніх кутів при цих же вершинах 11:9.
Знайти в градусах третій внутрішній кут трикутника.
Розв'язання: Задано трикутник ABC, у якого ∠A:
∠A:∠B=2:3, а відношення зовнішніх кутів при цих це вершинах ∠KAC:
∠NBC=11:9 (за умовою).
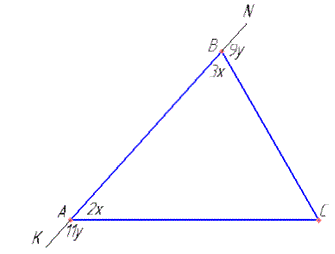
Позначимо: ∠A=2x, ∠B=3x, де x - коефіцієнт пропорційності внутрішніх кутів;
∠KAC=11y, ∠NBC=9y де y - коефіцієнт пропорційності зовнішніх кутів.
При одній вершині трикутника внутрішній і зовнішній кут є парою суміжних кутів, тому їх сума дорівнює 1800, тобто
∠A+ ∠KAC=180, звідси 2x+11y=180 (1)
∠B+ ∠NBC=180, звідси 3x+9y=180 (2)
Об'єднаємо (1) і (2) у систему рівнянь і знайдемо x, y:
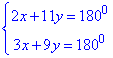
поділимо друге рівняння системи на 3, отримаємо
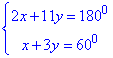
помножимо друге рівняння системи на -2, отримаємо
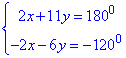
до другого рівняння системи додамо перше
5y=60, звідси y=12,
з другого рівняння другої системи маємо
x=60-3•12=24.
Отже, отримали ∠A=2 •24=48, ∠B=3•24=72.
За теоремою про суму кутів трикутника знайдемо третій внутрішній кут C:
∠C=180- ∠A-∠B=180-48-72=60,
∠C=60.
Відповідь: 60
Задача 39.39 Промінь світла падає від ліхтарика на поверхню дзеркала A під кутом 700, а відбитий від нього промінь падає на поверхню іншого дзеркала B під кутом 600 і відбивається від нього.
Дзеркала розміщені так, що всі падаючі та відбиті промені лежать в одній площині (див. рис.).
Знайти градусну міру найменшого внутрішнього кута утвореного променями трикутника ABC.
Розв'язання: Згідно із законами геометричної оптики: кут падіння променя дорівнює куту відбивання.
Зробимо математичну модель задачі: промені замінимо на сторони трикутника ABC, а площини дзеркал A та B на прямі LK та MN відповідно (проекція дзеркал на площину дії променів).
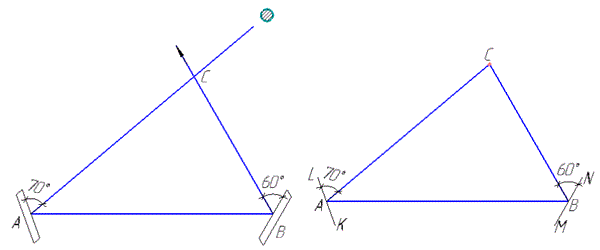
Тоді, за умовою задачі, ∠CAL=70 і ∠CBN=60, а за властивістю геометричної оптики:
∠BAK=∠CAL=70 і ∠ABM=∠CBN=60.
Оскільки кути ∠LAK і ∠NBM розгорнуті, то за властивістю вимірювання кутів отримаємо градусні міри внутрішніх кутів ΔABC:
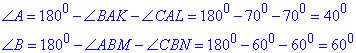
За теоремою про суму кутів ΔABC знайдемо ∠C:
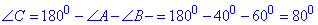
Отже, ∠A=40 - найменший внутрішній кут утвореного променями ΔABC.
Відповідь: 400
Приклад 32.1д Знайти кути чотирикутника ABCD, вписаного в коло, якщо ∠CBD=48, ∠ACD=34, ∠BDC=64.
Розв'язування: Маємо чотирикутник ABCD, який вписаний в коло з центром O.
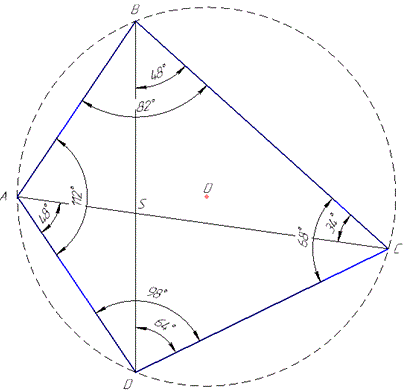
Із ΔBCD за теоремою про суму кутів трикутника встановлюємо∠C, єдиний який поки що можемо визначити:
∠C=180-∠CBD-∠BDC=180-48-64=68,
звідси отримаємо ∠ACB=∠ACD=68-34=34.
Оскільки чотирикутник ABCD вписаний в коло, то суми його протилежних кутів дорівнюють 180 градусів, звідси отримаємо
∠A=180-∠C=180-68=112.
Розглянемо кути ∠CBD і ∠CAD. Вони є вписаними кутами в коло і спираються на одну й ту ж хорду CD, тому за властивістю ∠CAD=∠CBD=48.
Аналогічно кути BDC і BAC. Вони також вписані в коло і спираються на одну й ту ж хорду BC, звідси за властивістю ∠BAC=∠BDC=64.
Із ΔABC за теоремою про суму кутів трикутника встановлюємо:
∠B=180-∠BAC-∠ACB=180-64-32=82.
Із ΔACD за теоремою про суму кутів трикутника встановлюємо ∠D:
∠D=180-∠CAD-∠ACD=180-48-34=98.
Відповідь: ∠A=112, ∠B=82, ∠C=68, ∠D=98.
Сподіваюсь Ви знайшли потрібні підказки. На сайті опубліковано чимало завдань, які необхідно вміти розв'язувати.
Залишайтеся з нами і поступово ми навчимо Вас розв'язувати завдання різної складності.
