Дослідження функції

Дослідження функції, побудова графіка

Wed, 08 Jul 2015 18:07:09 +0300

Дослідження функцій займає немало часу при розв'язуванні контрольних, домашніх завдань і щоб навчитися швидко розв'язувати потрібна інструкція, яка пояснює порядок дій і для чого це потрібно. Така інструкція розроблена викладачами і узагальнена на всі типи функцій вже давно, а ми її називаємо – загальна схема дослідження функції.

Щоб дослідити функцію y=f(x) та побудувати її графік необхідно:

1) знайти область визначення функції, тобто множину всіх точок для яких існує значення функції;

2) знайти (якщо вони існують) точки перетину графіка з координатними осями. Для цього потрібно у рівняння y=f(x) підставити x=0, а також розв'язати рівняння f(x)=0 для відшукання точок перетину з віссю абсцис Ox;

3) дослідити функцію на періодичність, парність і непарність. У деяких випадках це можна зробити візуально за самим виглядом функції, якщо ні - то проводимо перевірку:
1. f(-x)=f(x) – функція парна;

2. f(-x)=-f(x) – функція непарна;

3. f(x+T)=f(x) – функція періодична, T– період функції.

Таким чином, якщо маємо парну функцію y=f(x), то достатньо побудувати її для додатніх значень x>0, після чого відобразити симетрично відносно осі абсцис y на решту області. У випадку непарної функції графік буде симетричний відносно початку координат. Для прикладу, якщо маємо непарну функцію, графік якої належить першій чверті другу половину отримаємо поворотом першої чверті на 180 градусів (третя чверть).

Періодичними є переважно фукнкції, складені з простих тригонометричних та деякі параметрично задані функції.

4) знайти точки розриву та дослідити їх (такими точками є краї інтервалів визначення функції);

5) знайти інтервали монотонності, точки екстремумів та значення функції в цих точках;

6) знайти інтервали опуклості, вгнутості та точки перегину;

7) знайти асимптоти кривої;

8) побудувати графік функції.

Більшість з цих пунктів розлядалася на практиці в попередніх статтях, тому детально розписувати ми їх не будемо. Також не переживайте, якщо знайдете план в літературі чи інтернеті, який містить більше або менше пунктів. Пам'ятайте, що мета їх всіх – допомогти при побудові графіка функції.

Графіки елементарних функцій

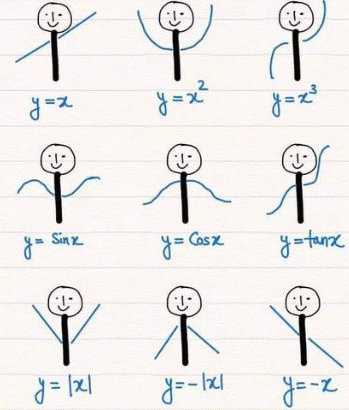
Перейдемо до практичної частини і досслідимо за схемою функцію.

Приклад 1. Дослідити функцію і побудувати її графік
(Дубовик В.П., Юрик І.І. "Вища математика. Збірник задач" )

І (5.889)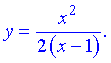

Розв'язання: 1) Функція визначена всюди, крім точки в якій знаменник перетворюється в нуль x=1. Область визначення складається з двох інтервалів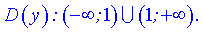
2) При підстановці x=0 знайдемо значення функції

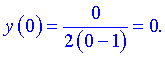
Таку ж саму точку отримаємо, якщо прирівняємо функцію до нуля. Точка x=0- єдина точка перетину з осями координат.
3) Перевірка на парність

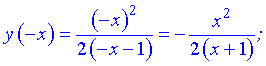
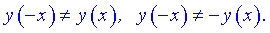
Отже функція ні парна, ні непарна, неперіодична.
4) В даному випадку маємо одну точку розриву x=1. Обчислимо границі зліва і справа

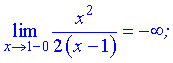
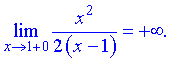
Отже x=1 – точка розриву другого роду.
5) Для відшукання інтервалів монотонності обчислюємо похідну функції

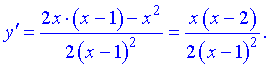
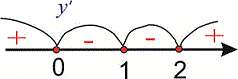
Прирівнюючи її до нуля матимемо точки підозрілі на екстремум x=0; x=2. Вони розбивають область визначення на інтервали монотонності

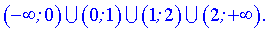
Дослідимо поведінку похідної справа та зліва від знайдених точок

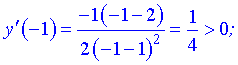
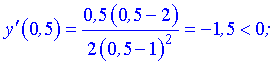
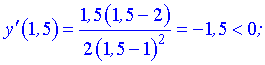
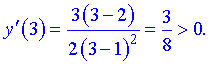
Графічно інтервали монотонності матимуть вигляд

Досліджувана функція зростає на інтервалах 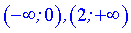та спадає .

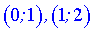Точка x=0 – точка локального максимуму, x=2 – локального мінімуму. Знайдемо значення функції

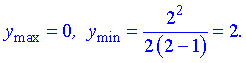
6) Для відшукання інтервалів опуклості знайдемо другу похідну

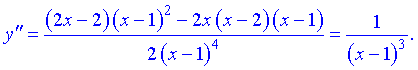
Друга похідна не перетворюється в нуль, а це значить, що функція немає точок перегину.
Проте, це не означає, що функція не є опуклою та вгнутою, детальні пояснення містяться в публікації
Як визначати інтервали опуклості та вгнутості функції?
Зліва від одиниці на інтервалі (-infinity;1) друга похідна менша нуля (перевіряється підстановкою), звідси робимо висновок, що функція опукла.
Після одиниці друга похідна додатна, отже на інтервалі (1; +infinity) функція вгнута.
Як це виглядає на графіку Ви можете побачити з наведеного далі рисунку.

7) Точка x=1 – векртикальна асимптота функції. Рівняння похилої асимптоти має вигляд
y=kx+b
де k, b - границі, що знаходять за правилом

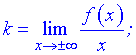
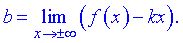
Знаходимо границі

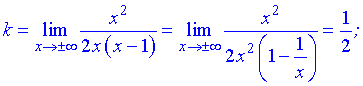
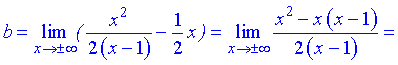
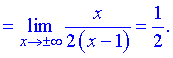
Кінцевий вигляд прямої

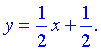
8) На основі проведеного аналізу виконуємо побудову графіка функції.

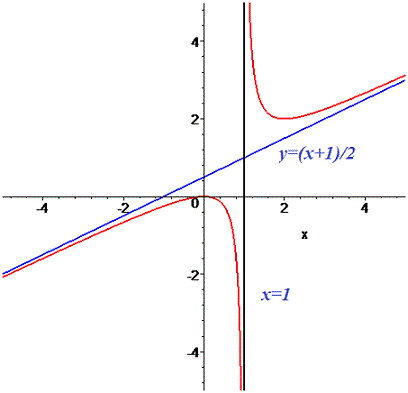
Користуйтеся загальною схемою дослідження функції на практиці, розв'язуйте подібні приклади самостійно. Це дозволить в короткий час освоїти даний матеріал. Інші приклади по даній тематиці Ви знайдете в наступних статтях.

Розвязування задач на найбільше та найменше значення функції на відрізку

Wed, 08 Jul 2015 18:15:37 +0300

Відшукання максимумів та мінімумів – одне з поширених завдань при дослідженнях функцій.
Неперервна на відрізку [a;b] функція y=f(x) набуває своїх найбільшого та найменшого значень, або в критичних точках (у точках, в яких похідна перетворюється в нуль чи не існує), що належать досліджуваному проміжку, або на його кінцях x=a, x=b.
На практиці знаходження максимумів та мінімумів подібне до відшукання локального екстремуму, тільки добавляються краї проміжку. Можливі випадки коли максимуми та мінімуми функцій знаходяться в точках локального екстремуму, а можливі - на краях відрізку.
Розглянемо ряд прикладів, щоб ознайомити Вас з методикою дослідження.

-----------------------------------

Приклади. Визначити найбільше та найменше значення фунції на проміжку.

Збірник В.Ю. Клепко, В.Л. Голець "Вища математика в прикладах і задачах".

1. (4.55.б)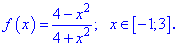

Розв'язування: Функція визначена на всій множині дійсних чисел 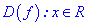. Хоча вона і дробова, проте знаменник ніде не перетворюється в нуль.
Знайдемо похідну функції

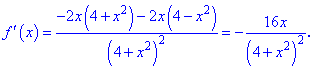
Прирівняємо її до нуля та визначимо критичні точки

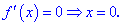
Перевіримо знак похідної зліва та справа від знайденої точки

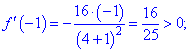
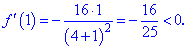
Похідна при переході через точку x=0 змінює знак з додатного "+" на від'ємний "-", отже вона є точкою локального максимуму.
Знайдемо значення функції в точці x=0

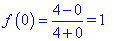
та на краях відрізку

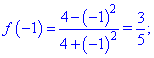
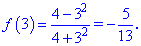
Таким чином функція досягає максимуму в точці локального екстремуму f_max(0)=1, а мінімуму на одному з країв відрізку f_min(3)=-5/13.
Для повного представлення, що ми досліджуємо, побудуємо графік функції на інтервалі в математичному пакеті Мaple:
restart; with(plots);
plot((4-x^2)/(4+x^2),x=-2..4);
В результаті отримаємо графік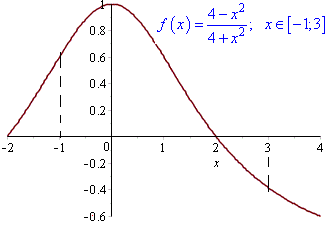

Дослідження на максимуми та мнімуми теж можна проводити в Мaple, але проце поговоримо на іншому уроці.

2. (4.55.д)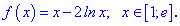

Розв'язування: На заданому проміжку функція визначена всюди, обчислимо її похідну

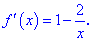
З умови рівності похідної нулю знаходимо критичну точку

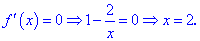
Задана точка належить розглянутому відрізку. Знайдемо значення функції в критичній точці та на краях

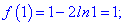
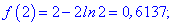
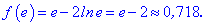
Функція набуває максимуму і мінімуму в точках
f_max(1)=1, f_min(2)=0,6137.
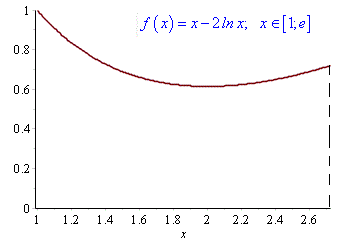
Побудуємо графік функції в Мaple
plot(x-2*ln(x), x = 1 .. exp(1), 0 .. 1);

3. (4.55.є)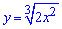

Розв'язування: Функція визначена для всіх значень аргумента .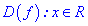
Знайдемо похідну

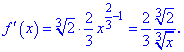
З виразу бачимо, що похідна відмінна від нуля на проміжку визначення, однак в точці x=0 вона не існує.
Обчислимо значення функції в підозрілих на екстремум точках

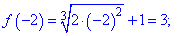
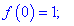
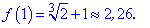
Найбільше значення функція приймає в точці f_max(-2)=3 , а найменше значення в критичній точці f_min(0)=1.
Графік досліджуваної функції наведено нижче
plot((2*abs(x))^(2/3), x = -2 .. 1);

Наведемо розв'язки задач із збірника Дубовик В.П., Юрик І.І. "Вища математика" .

4. (5.770)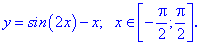

Розв'язування: Синус функція визначена всюди, тому приступаємо до знаходження похідної

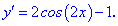
Прирівняємо її до нуля та знайдемо критичні точки

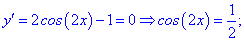
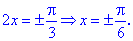
Знайдемо значення функції у всіх підозрілих на екстремум точках

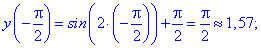
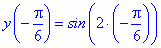
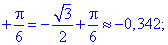
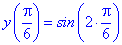
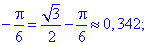
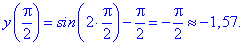
З отриманих значень випливає, що функція приймає максимум та мінімум на краях відрізку

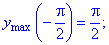
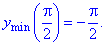
Побудуємо графік функції
plot(sin(2*x)-x, x = -(1/2)*Pi .. (1/2)*Pi);

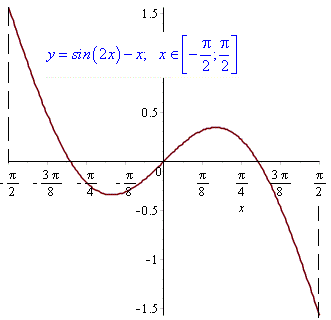
5. (5.771)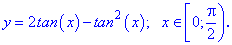

Розв'язування: На заданому інтервалі функція визначена, тому переходимо до диференціювання

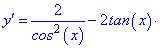
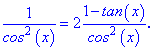
Прирівнявши до нуля похідну отримаємо

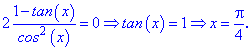
Іншу критичну точку знайдемо з умови, що похідна не існує

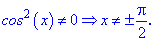
Одна співпадає з початком відрізку. Обчислимо значення функції на краях відрізку та в критичних точках

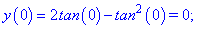
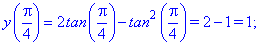
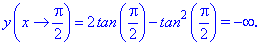
Таким чином функція приймає максимальне значення в критичній точці, а мінімальне на кінці відрізку

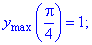
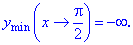
Виконаємо побудову графіка функції в Maple
plot(2*tan(x)-tan(x)^2, x = 0 .. (1/2)*Pi);

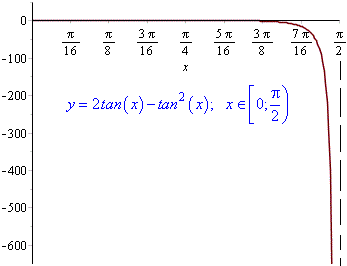
З наведених розв'язків можна зробити висновки, що головним в обчисленні є знання функцій та вміння диференціювати. Все решта зводиться до відшукання значень функцій в точках та аналізу результатів. Вивчайте властивості елементарних функцій, правила знаходження похідних, це Вам стане в нагоді при знаходженні екстремумів.

Точки розриву функції першого та другого роду

Wed, 08 Jul 2015 18:10:58 +0300

Функція f(x) називається неперервною в точці х=а, якщо:
1) вона визначена в цій точці;
2) існує границя функції в цій точці

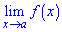
3) значення границі дорівнює значенню функції в точці х=а, тобто

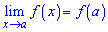
Якщо одна із умов порушується, то функція називається розривною в точці х=а, а сама точка х=а називається точкою розриву. Усі елементарні функції є неперервними на інтервалах визначеності.

КЛАСИФІКАЦІЯ ТОЧОК РОЗРИВУ

Точка х₀ називається точкою розриву першого роду функції у = f(x), якщо існують скінчені односторонні границі справа

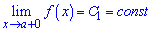
та зліва
.

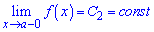Якщо, крім того, виконується хоча б одна із умов

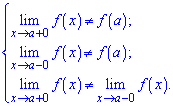
то функція в точці х=а має неусувний розрив першого роду.

Якщо границі функції рівні проте функція не існує

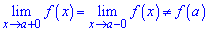
то маємо усувний розрив першого роду.

Точка х0 називається точкою розриву другого роду функції у= f(x), якщо границя справа 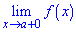або зліва 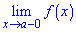не існує або нескінченна.

Стрибком функції в точці розриву х=х₀ називається різниця її односторонніх границь

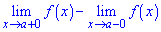
якщо вони різні.

Правила знаходження точок розриву функції

1) елементарна функція може мати розрив тільки в окремих точках, але не може бути розривною на певному інтервалі.
2) елементарна функція може мати розрив в точці де вона не визначена за умови, що вона буде визначена хоча би з однієї сторони від цієї точки.
3) неелементарна функція може мати розриви як в точках, де вона невизначена, так і в тих, де вона визначена.
Наприклад, якщо функція задана кількома різними аналітичними виразами (формулами) для різних інтервалів, то на межі стику може бути розривною.

Приклади знаходження точок розриву функції

Завдання 1.Знайти точки розриву функції
а)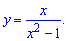

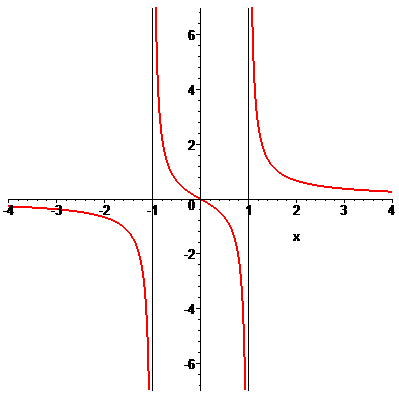
Розв'язання: Функція визначена в усіх точках крім тих де знаменник перетворюється в нуль x=1,x=-1. Область визначення функції наступна

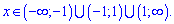
Знайдемо односторонні границі в точках розриву

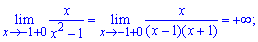
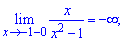
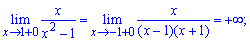
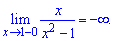
При знаходженні односторонніх границь подібного вигляду достатньо переконатися в знаку функції та в тому, що знаменник прямує до нуля. В результаті отримаємо границю рівну безмежності або мінус безмежності.
Оскільки в точках x=1,x=-1 функція має нескінченні односторонні границі, то аргументи x=1,x=-1 є точками розриву ІІ роду. Графік функції наведено на рисунку нижче

б)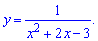

Розв'язання: Завдання подібне до попереднього. В першу чергу знаходимо нулі знаменника

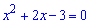
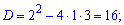
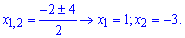
Таким чином функція визначена на всій дійсній осі за виключенням точок x=-3; x=1, які є точками розриву. Обчислимо односторонні границі справа та зліва

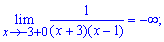
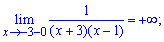
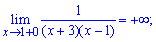
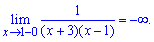
Границі функції нескінченні, тому, за означенням, маємо точки розриву x=-3; x=1 другого роду.

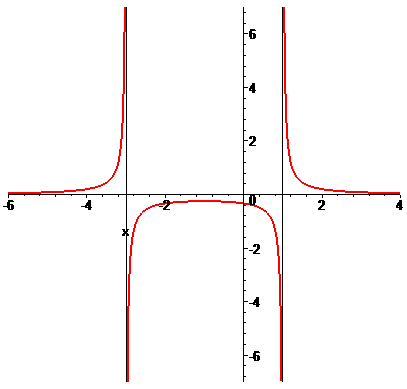
Із графіків наведених функцій бачимо, що для ряду з них відшукання точок розриву еквівалентне знаходженню вертикальних асимптот. Але бувають функції, які і без вертикальних асимптот мають розриви першого чи другого роду.

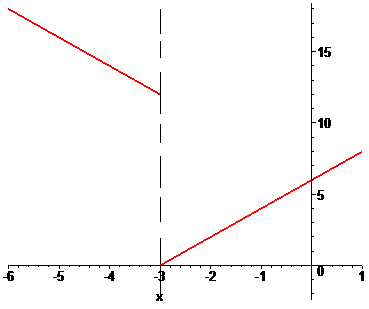
в)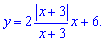

Розв'язання: Задана функція неперервна на всій числовій осі крім точки x=-3. Обчислимо односторонні границі в цій точці

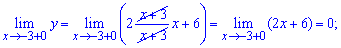
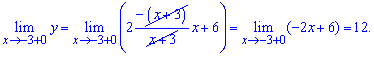
Вони різняться за значеннями, проте є скінченними. Отже точка x=-3 є неусувною точкою розриву І роду.

Завдання 2.Знайти точки розриву функції, якщо вони існують. Обчислити стрибок функції в точці розриву. Побудувати графік функції.

а)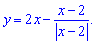

Розв'язання:Для заданої дробової функції з модулем в знаменнику точка x=2 є точкою розриву. Знайдемо границі, щоб визначити характер розриву

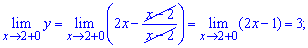
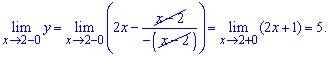
За означенням, точка x=2 є неусувною точкою розриву першого роду. Обчислимо стрибок функції при x=2

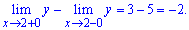
Графік функції на інтервалі, який нас цікавить наведено далі

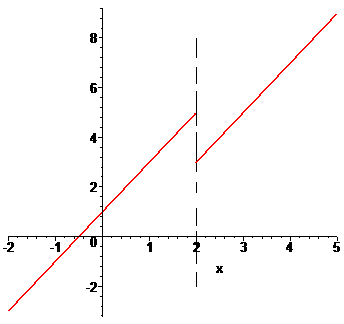
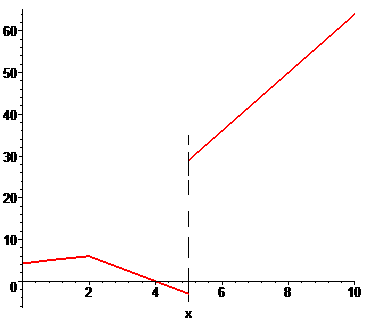
б)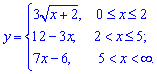

Розв'язання: Неелементарна функція y(x) визначена для всіх невід'ємних значень аргументу. Точки, які розбивають функцію на інтервали можуть бути розривами. Для перевірки знайдемо відповідні границі

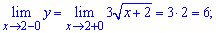
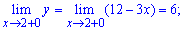
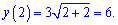
Оскільки границі в точці x=2 рівні значенню функції в цій точці, то функція – неперервна.
Звідси також слідує, що для вихідної функції стрибок рівний 6-6=0.
Дослідимо на неперервність другу точку

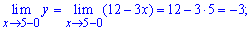
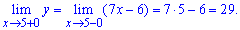
За означенням функція в точці x=2 має неусувний розрив І роду.
Стрибок функції рівний 29-(-3)=31.
Для заданої функції побудовано графік.

З наведеного матеріалу Ви повинні навчитися знаходити розриви першого та другого роду, а також розрізняти їх. Для цього підібрано небагато прикладів, які в повній мірі розкривають всі важливі питання теми. Все решта зводиться до знаходження простих односторонніх границь і не повинно бути для Вас складним.

Застосування похідної для дослідження функції

Wed, 08 Jul 2015 18:17:51 +0300

Без похідної неможливо визначити проміжки зростання та спадання функції, точки перегину, якщо такі існують. Суть таких досліджень – полегшити побудову графіка функції, адже якщо Ви знайшли вказані проміжки то на їх межі функція має локальні екстремуми і залишається знайти в них значення і побудувати графік функції. Правила на знаходження інтервалів зростання функції достатньо прості та зрозумілі кожному.

Ознака зростання функції

Якщо похідна функції більша нуля f'(x)> 0 на деякому проміжку, то функція f (x) зростає на цьому проміжку.

І обернене твердження.

Ознака спадання функції

Якщо похідна функції від'ємна f'(x) < 0 на деякому інтервалі, то функція f (x) спадає на даному інтервалі.

Застосування похідної на прикладах

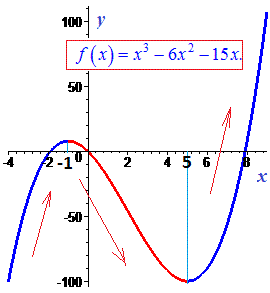
Приклад 1. Знайти проміжки зростання та спадання функції
f(x)=x³-6*x²-15x.
Розв'язання: Обчислюємо похідну функції за змінною

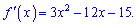
Прирівняємо похідну до нуля та визначимо стаціонарні точки

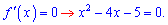
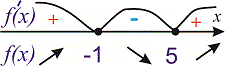
За теоремою Вієта корені квадратного рівняння рівні x=-1; x=5.
Точки розбивають числову вісь на три інтервали

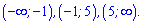
Знак похідної визначаємо підстановкою точки з інтервалу.

Запам'ятайте: для швидкого визначення знаку похідної завжди вибирайте нуль, якщо він не є стаціонарною точкою або іншу точку, в якій легко обчислити значення похідної.

В нулі похідна менша нуля

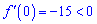
отже на інтервалі (-1;5) функція спадає, а на двох сусідніх 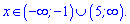зростає

Графік функції має вигляд

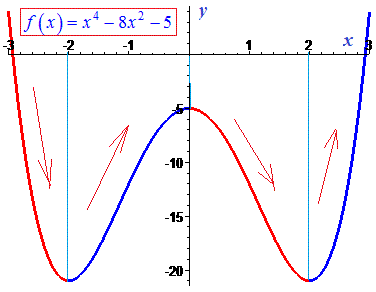
Приклад 2. Дослідити функцію f(x)=x⁴-8*x²-5 та знайти проміжки зростання.
Розв'язання: Задана функція є парною

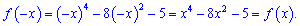
Знайдемо інтервали монотонності функції. Для цього обчислимо похідну

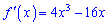
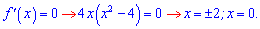
Отримали три точки, які розбивають числову вісь на 4 інтервали

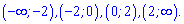
Знак похідної визначаємо підстановкою одиниці

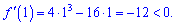
Отже на інтервалі (0;2) функція спадає, на сусідніх інтервалах знаки похідної чергуються

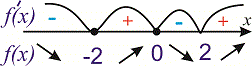
У відповіді отримаємо 2 інтервали зростання функції

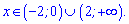
Для наочності графік функції наведено нижче

Інше застосування похідної відноситься до знаходження інтервалів опуклості та вгнутості графіка функції. При цьому потрібно знаходити другу похідну та виконувати відповідний аналіз.

Локальний екстремум функції. Правила знаходження

Wed, 08 Jul 2015 18:16:51 +0300

Відшукання локальних максимумів і мінімумів не обходиться без диференціювання і потрібне при дослідженні функції та побудові її графіка.

Точка x₀ називається точкою локального максимуму (або мінімуму) функції y=f(x), якщо існує такий окіл 0<|x-x₀| цієї точки, який належить області визначення функції, і для всіх аргументів x0 з цього околу виконується нерівність f(x)0) (або f(x)>f(x₀)).

Точки максимуму і мінімуму називаються точками екстремуму функції , а значення функції в екстремальних точках – її екстремальними значеннями.

НЕОБХІДНА ОЗНАКА ЛОКАЛЬНОГО ЕКСТРЕМУМУ:

Якщо функція має в точці x₀ локальний екстремум, то її похідна або рівна нулю f'(x₀)=0 , або не існує. Точки, які задовольняють виписаним вище вимогам ще називають критичними точками. Проте не в кожній критичній точці функція має екстремум. Відповідь на питання: чи буде критична точка точкою екстремуму дає наступна теорема.

ДОСТАТНЯ ОЗНАКИ ІСНУВАННЯ ЕКСТРЕМУМУ ФУНКЦІЇ

Теорема І. Нехай функція y=f(x) неперервна в деякому інтервалі, що містить критичну точку x₀, і диференційована у всіх точках цього інтервалу (за винятком, можливо, самої точки x₀). Тоді для точки x₀ функція має максимум, якщо для аргументів x0 виконується f'(x₀)>0, а для x>x₀ умова f'(x₀)<0.

Якщо ж для x0 похідна менша нуля f'(x₀)<0 , а для x>x₀ більша нуля f'(x₀)>0, то для точки x=x₀ функція має мінімум.

Теорема ІІ. Нехай функція два рази диференційована в околі точки x₀ і похідна рівна нулю f'(x₀)=0 . Тоді в точці x=x₀ функція має локальний максимум, якщо друга похідна менша нуля f"(x₀)<0 , і локальний мінімум, якщо друга похідна додатна f"(x₀)>0.

Якщо ж f"(x₀)=0, то точка x=x₀ може й не бути точкою екстремуму.
При дослідженні функцій на екстремуми використовують обидві теореми. Перша на практиці простіша, оскільки не вимагає знаходження другої похідної.

ПРАВИЛА ЗНАХОДЖЕННЯ ЕКСТРЕМУМІВ (МАКСИМУМІВ І МІНІМУМІВ) ЗА ДОПОМОГОЮ ПЕРШОЇ ПОХІДНОЇ

1) знайти область визначення D(f);
2) знайти похідну f'(x);
3) знайти критичні точки x₀;
4) дослідити знак похідної f'(x) на інтервалах, які отримали від розбиття критичними точками області визначення.

При цьому критична точка x₀ є точкою мінімуму, якщо при переході через неї зліва направо f'(x) змінює знак з від'ємного "-" на додатній "+", в протилежному випаду x₀ є точкою максимуму.
Замість даного правила можна визначати другу похідну f"(x) і досліджувати згідно другої теореми.

5) обчислити значення функції в точках екстремуму.

Розглянемо тепер дослідження функції на екстремуми на конкретних прикладах.

Приклади. Збірник В.Ю. Клепко, В.Л. Голець "Вища математика в прикладах і задачах"

1. (4.53.7) y=x²e^-x

Ров'язування: 1) Областю визначення буде множина дійсних чисел D(y): x∈R
2) Знаходимо похідну функції

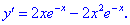
3) Прирівнявши її до нуя, визначаємо критичні точки

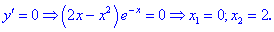
Вони розбивають область визначення на такі інтервали

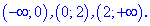
4) Дослідимо знак похідної на знайдених інтервалах методом підстановки внутрішніх точок

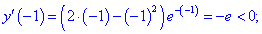
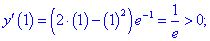
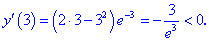
Таким чином перша точка x=0 є точкою мінімуму, а друга x=2 - точкою максимуму.
5) Обчислюємо значення ординати точкок

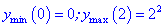
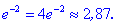
На цьому і грунтуються дослідження функцій на екстремуми.
Далі навчимо Вас будувати графіки, асимптоти і виконувати дослідження функції в математичному пакеті Мейпл.
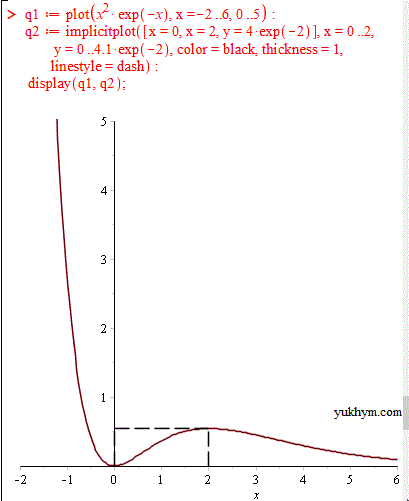
Для побудови першої функції на інтервалі, де добре видно локальний максимум скористаємося наступним кодом:
restart; with(plots);
q1 := plot(x^2*exp(-x), x = -2 .. 6, 0 .. 5);
q2 := implicitplot([x = 0, x = 2, y = 4*exp(-2)], x = 0 .. 2, y = 0 .. 4.1*exp(-2), color = black, thickness = 1, linestyle = dash);
display(q1, q2);
В результаті отримаємо графік на якому в точці x=0 маємо локальний мінімум, а в точці x=2 – локальний максимум.

2. (4.53.9) y=ln√(1+x^2)+arctan(x)

Ров'язування: 1) Областю визначення буде множина дійсних чисел D(y): x∈(-∞;+∞), оскільки корінь завжди більший одиниці

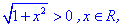
і функція арктангенс визначена на всій дійсній осі .

2) Знаходимо похідну логарифма та арктангенса

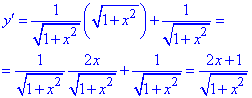
3) З умови рівності похідної нулю знаходимо критичну точку
2x+1=0, x=-1/2=-0,5.
Вона розбиває область визначення на два інтервали
x∈(-∞;-0,5)∪(0,5;+∞).
4) Визначимо знак похідної в кожній з областей

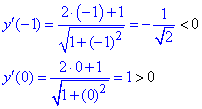
Отже в критичній точці x=-0,5 функція приймає мінімальне значення.
5) Обчислимо екстремум функції
y(-0.5)=ln(1+(-0,5)^2)+arctan(-0,5)≈-0,2405
Ще одне завдання детально проаналізована на локальний екстремум.
Для наочності, покажемо як виглядає локальний мінімум на графіку.
Для цього в Мейплі наберемо наступний код та обчислимо
q1 := plot(ln(x^2+1)+arctan(x), x = -8 .. 5);
q2 := implicitplot([x = 0, 5], x = -5 .. 5, y = -1 .. 0, color = black, thickness = 1, linestyle = dash);
display(q1, q2);
Отримаємо наступний графік функції

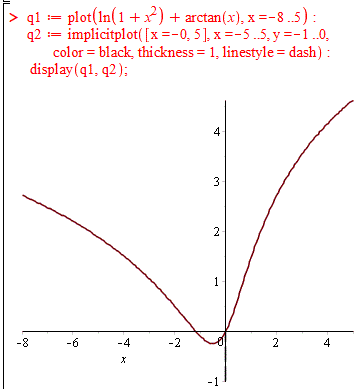
3. (4.53.13)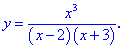

Ров'язування: 1) Функція визначена коли знаменник дробу не перетворюється в нуль
(x-2)(x+3)≠0⇒x=2, x=-3.
Отже область визначення складається з трьох інтервалів
D(y): x∈(-∞;-3)∪(-3;2)∪(2;+∞)
2) Обчислимо похідну

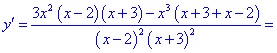
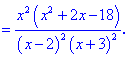
3) Прирівнюємо похідну до нуля і знаходимо критичні точки.

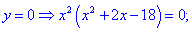
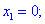
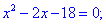
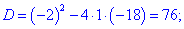
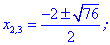
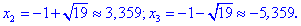
4) Встановлюємо знак похідної в кожній з областей підстановкою відповідних значень.

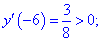
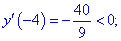
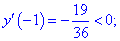
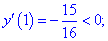
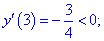
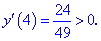
Таким чином перша точка x₃=-5,359 є точкою локального максимуму, а x₂=3,359 локального мінімуму. В x₁=0 маємо перегин функції, але про нього буде більше матеріалу в наступних статтях.
5) Знаходимо значення в критичних точках

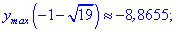
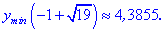
Незважаючи на те, що значення функції y_maxmin, перша точка є точкою локального максимуму, а дуга – мінімуму. Не лякайтеся, якщо в Вас вийдуть подібні результати, при визначенні локальних екстремумів такі ситуації нормальне явище.
Побудуємо графік функції разом з вертикальними асимптотами в Мейплі:
q1 := plot(x^3/(-2+x)/(x+3), x = -8 .. 8, discont = true);
q2 := implicitplot([x=-3,x = 2], x = -5 .. 5, y = -30 .. 30, color = black, thickness = 1, linestyle = dash);
display(q1, q2);

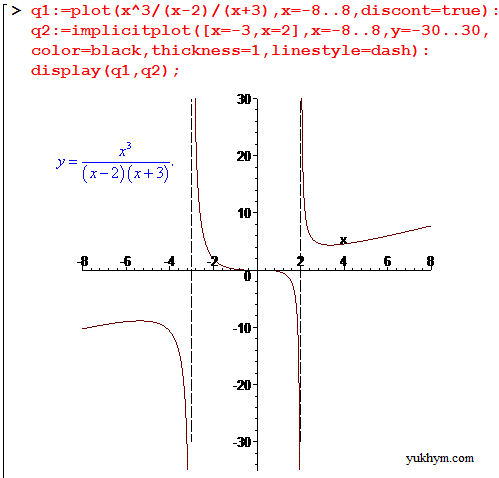
З графіку бачимо, що функція має похилу асимптоту, але як про те як скласти рівняння похилих асимптот поговоримо в наступнй статті.
Попереду Вас чекає багато готових розв'язків на повне дослдження функції, знаходження асимптот, інтервалів опуклості та вгнутості. Тож залишайтеся з нами та беріть максимум користі для навчання зі сторінок сайту!

Побудова графіків функцій методом геометричних перетворень

Tue, 31 Mar 2020 20:02:27 +0300

Основними методами геометричних перетворень графіків функцій є симетрія відносно осей Ox, Oy;
паралельне перенесення відносно осей Ox, Oy;
стиск та розтяг графіків відносно осей; відображення частини графіка під віссю Ox нагору (аналог модуль функції) і навпаки;
поворот площини навколо певної точки. В шкільному курсі Вас навчають як геометричні перетворення використовувати до графіків функцій та як це впливає на область визначення та область значень. Всі перелічені вище перетворення необхідні, щоб швидко навчити Вас будувати графіки функцій.

Основні геометричн перетворення графіка функцї

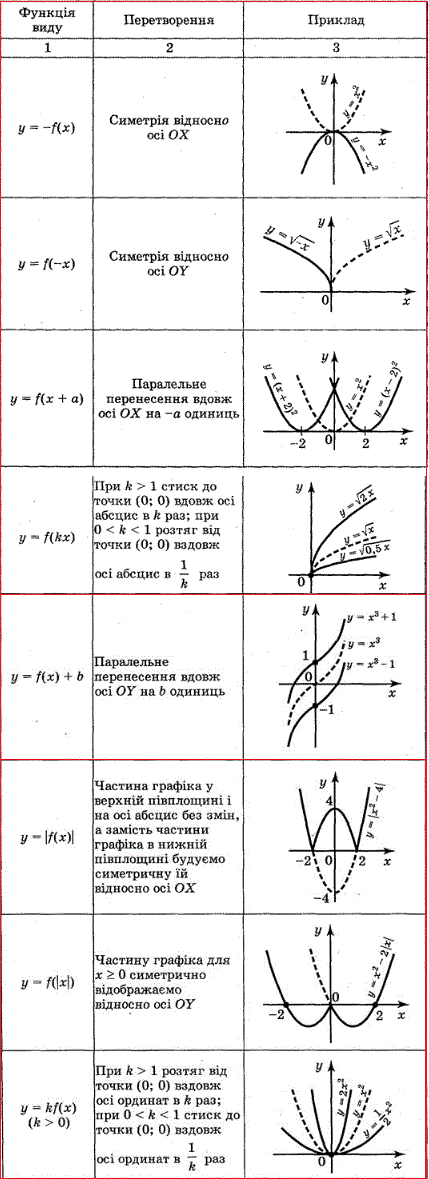
Для повторення шкільних матеріалів, які Ви повинні вільно вміти використовувати, уважно перегляньте таблицю в якій проілюстровані вісім основних перетворень графіка функції у = f(x):
у = -f(x); у = f(-x); у = f(x) + b; у = f(x + a); у = af(x); у = f(ax); у = f(|x|); у =|f(x)|.

Переходимо до практики застосування геометричних перетворень для графіків функцій та проаналізуємо готові відповіді до завдань із ЗНО підготовки. Завдання добре розписані, крім того основні методи перетворень виділені в ході розв'язування завдань. Всього розв'язано 33 приклади, частина з яких увійшли до наступних публікацій.

Побудова графіків функцій за допомогою геометричних перетворень

Приклад 23.1 Вказати формулу функції, графік якої отримують із графіка y=1/x у результаті його паралельного перенесення в додатному напрямі осі Oy на 5 одиниць.

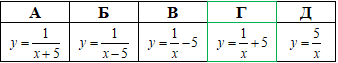
Розв'язування: Графік функції y=f(x)+a можна одержати із графіка функції y=f(x) за допомогою паралельного перенесення вздовж осі Oy на a одиниць угору (в додатному напрямі осі Oy), якщо a>0, і на a одиниць униз (у від’ємному напрямі осі Oy), якщо a<0.

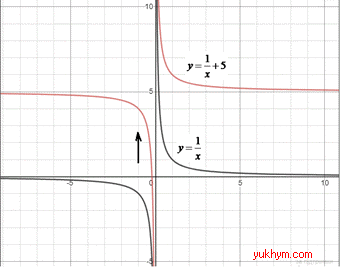
Отже, з графіка гіперболи y=1/x, у результаті його паралельного перенесення в додатному напрямі осі Oy на 5 одиниць, отримаємо графік функції y=1/x+5.
Це відповідає варіанту Г тестів.
Відповідь: y=1/x+5 – Г.

(В усіх завданнях графік чорним кольором є основним, а червоним кольором графік отриманий після геометричних перетворень)!

Приклад 23.2 На якому з наведених рисунків зображено ескіз графіка функції y=4-(x-1)^2?

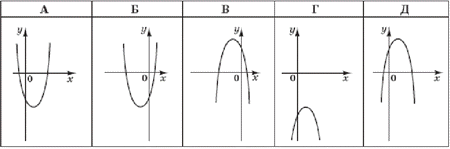
Розв'язування: Графік функції y=f(x+b) можна одержати із графіка функції y=f(x) за допомогою паралельного перенесення вздовж осі Ox на b одиниць праворуч (в додатному напрямі осі Ox), якщо b<0, і на b одиниць ліворуч (у від’ємному напрямі осі Ox), якщо b>0.

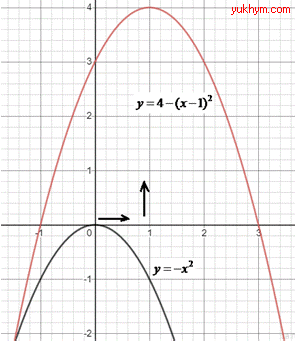
Отже, з графіка функції y=-x^2 (парабола) отримали y=4-(x-1)² паралельними перенесеннями на 1 одиницю праворуч і на 4 одиниці вгору, тобто на вектор p(1;4).
Відповідь: Д.

Приклад 23.4 Областю значень функції y=f(x) є проміжок [-4;16]. Знайти область значень функції y=1/4•f(x).

Розв'язування: Завдання на область визначення та область значень досить поширені, тому запам'ятайте схему обчислень.
Оскільки функцію y=1/4•f(x) отримують з функції y=f(x) стисненням у 4 рази до осі Ox, то область значень (множина y) теж стиснеться у 4 рази.
Формулами це може мати запис
-4•1/4≤1/4•f(x)≤16•1/4, звідси
-1≤1/4•f(x)≤4.
Замість f(x) можете використовувати в нерівностях y, такі позначення будуть рівносильні для області значень.
Отже, E(y)=[-1;4] - область значень функції 1/4•f(x).
Відповідь: [-1;4] – В.

Приклад 23.5 На якому з рисунків зображено графік функції y=-2^x?

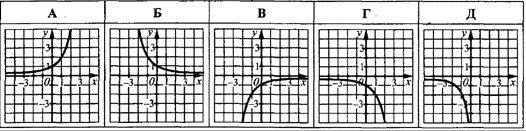
Розв'язування: Графік функції y=-f(x) можна одержати із графіка функції y=f(x) за допомогою симетричного відображення відносно осі Ox (абсцис).
Відповідний рисунок показникової функції до та після геометричного перетворення має вигляд.

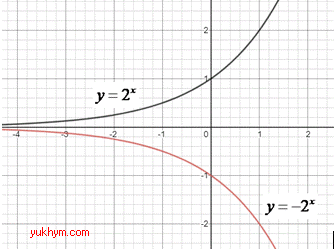
Відповідь: Г.

Приклад 23.6 Вказати формулу функції, графік якої отримують із графіка функції y=x^3 у результаті його паралельного перенесення в додатному напрямі осі Ox на 4 одиниці.

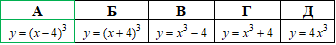
Розв'язування: З графіка функції y=x^3, у результаті його паралельного перенесення в додатному напрямі осі Ox на 4 одиниці, отримаємо функцію y=(x-4)^3.
Побудуємо зсув кубічної функції згідно умови.

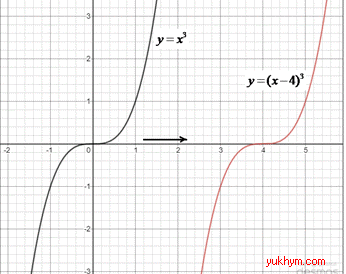
Відповідь: y=(x-4)^3 – А.

Приклад 23.7 На якому з рисунків зображено графік функції y=√(x+1)?

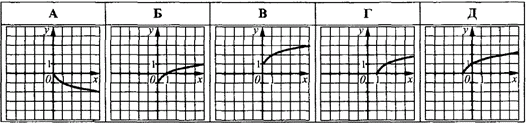
Розв'язування: З графіка функції y=√x, у результаті його паралельного перенесення у від’ємному напрямі осі Ox на 1 одиницю, отримаємо функцію y=√(x+1).

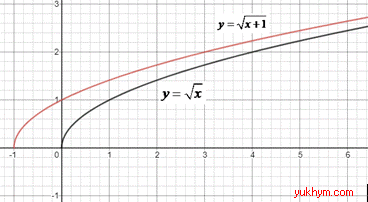
Відповідь: Д.

Приклад 23.8 Вказати формулу функції, графік якої отримують із графіка функції y=sin(x) у результаті його розтягування від осі Oy у 8 разів?

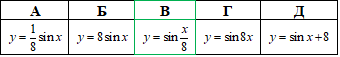
Розв'язування: Графік функції y=f(c•x) можна одержати із графіка функції y=f(x) за допомогою розтягу від осі Oy у c разів, якщо 0, і за допомогою стиснення до осі Oy у c разів, якщо c>1.

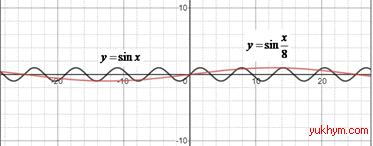
Отже, з графіка функції y=sin(x), у результаті його розтягу до осі Oy у 8 разів, отримаємо функцію y=sin(x/8).
Відповідь: y=sin(x/8)– В.

Приклад 23.9 Областю визначення функції y=f(x) є проміжок [-4;6].

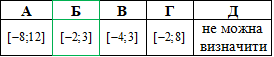
Знайти область визначення функції y=f(2x).
Розв'язування: Оскільки функцію y=f(2x) отримують з функції y=f(x) стисненням удвічі до осі Oy, то D(y)=[-2;3] - область визначення функції y=f(2x) (область визначення звузили у 2 рази).
Відповідь: [-2;3] – Б.

Приклад 23.10 На рисунку зображено ескіз графіка функції y=f(x). На якому з рисунків зображено ескіз графіка функції y=f(-x)?

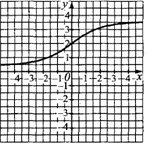
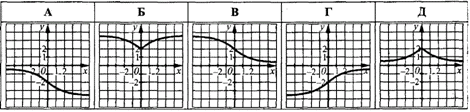
Розв'язування: Графік функції y=f(-x) можна одержати із графіка функції y=f(x) за допомогою симетричного відображення відносно осі Oy (ординат). Перегляньте уважно кожен з варіантів тестових відповідей та переконайтесь, що це В.
Відповідь: В.

Приклад 23.33 Найбільшим значенням функції y=f(x) є число 8. Знайти:
1) найбільше значення функції y=0,3f(4x+5)-1;
2) найменше значення функції y=-3f(2x-5).
Розв'язування: Область значень для функцій y=f(x), y=f(4x+5) і y=f(2x-5) однакова, оскільки змінення відбувається лише в межах осі Ox. Тому f(4x+5)≤8,
звідси
0,3•f(4x+5)≤0,3•8,
0,3•f(4x+5)≤2,4,
0,3•f(4x+5)-1≤2,4-1,
0,3•f(4x+5)-1≤ 1,4.
f(2x+5)≤8,
звідси
-3•f(2x+5) ≥-3•8,
-3•f(2x+5) ≥-24.
Отже, найбільшим значенням функції y=0,3f(4x+5)-1 є число 1,4;
найменшим значенням функції y=-3f(2x-5) є число -24.
Відповідь: 1,4; -24.

Попереду Вас чекають більше 20 готових прикладів на геометричні перетворення графіків функцій, що відповідають програмі ЗНО підготовки з математики.

Геометричні перетворення графіків функцій. ЗНО підготовка

Tue, 31 Mar 2020 19:48:35 +0300

Продовжуємо розбирати готові відповіді із ЗНО тестів на геометричні перетворення графіків функцій: паралельне перенесення, симетричне відображення, розтяг та стиск. Щоб не повертатися до попередніх десяти прикладів та теорії нагадаємо основні геометричні перетворення з ескізами відповідних графіків.

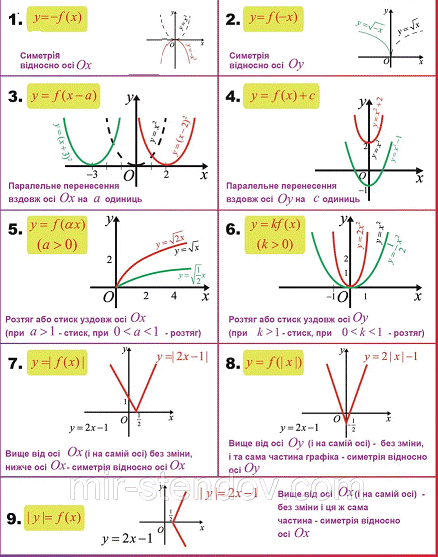
Таблицю можете завантажити та використовувати при розв'язуванні подібних завдань самостійно. А зараз перейдемо до розгляду тестових завдань із ЗНО підготовки з математики.

Приклад 23.11 На якому з рисунків зображено графік функції y=|log₂x|?

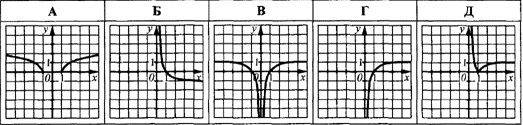
Розв'язування: Графік функції y=|f(x)| можна одержати із графіка функції y=f(x) наступним чином: ту частину графіка функції y=f(x), яка розміщена над віссю Ox, у тому числі точки перетину графіка з віссю абсцис, залишаємо без змін, а ту частину, яка розміщена під віссю абсцис, симетрично відображаємо відносно цієї осі (Ox).
Побудуємо логарифмічну функцію, та її модуль за допомогою інструкції виписаної вище.

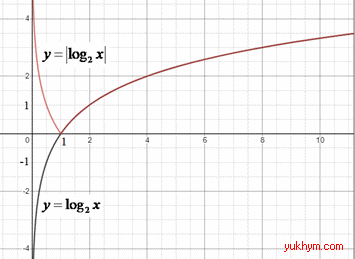
Відповідь: Д.

Приклад 23.12 На рисунку зображено графік функції y=f(x).

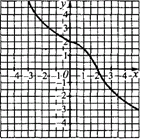
На якому з рисунків зображено графік функції y=f(|x|)?

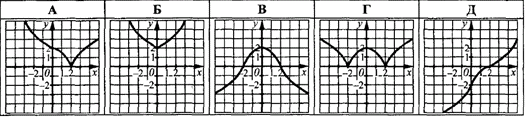
Розв'язування: Графік функції y=f(|x|) можна одержати із графіка функції y=f(x) наступним чином: ту частину графіка функції y=f(x), яка розміщена праворуч осі Oy, у тому числі точки перетину графіка з віссю ординат, залишаємо без змін, а ту частину, яка розміщена ліворуч від осі ординат (для від'ємних x), замінюємо симетричною до розташованої праворуч частини відносно осі ординат (Oy).
Із запропонованих тестових відповідей варіант В задовільняє правило.
Відповідь: В.

Приклад 23.13 Графік функції y=x^3 зсунули ліворуч на 4 одиниці й відобразили симетрично відносно осі Ox. Графік якої функції отримали в результаті таких перетворень?

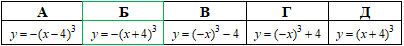
Розв'язування: Щоб отримати графік функції y=(x+4)³ необхідно графік y=x³ зсунути ліворуч на 4 одиниці.
Графік функції y=(x+4)^3 відобразили симетрично відносно осі Ox, отримаємо y=-(x+4)^3.

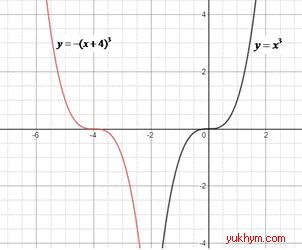
Відповідь: y=-(x+4)^3 – Б.

Приклад 23.14 Областю значень функції y=f(x) є проміжок [-2;2].
Знайти область значень функції y=4f(x)-3.

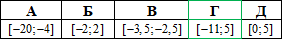
Розв'язування: Будьте уважними та прослідкуйте як змінюється область визначення та область значень при геометричних перетвореннях графіків функцій.
Оскільки функцію y=4f(x)-3 отримують з функції y=f(x) розтягом останньої у 4 рази до осі Ox та зсуненням на 3 одиниці вниз (відносно осі Oy), то запишемо як мінятиметься область значень при цьому
-2≤f(x)≤2,
-2•4≤4•f(x)≤2•4, тобто -8≤4•f(x)≤8,
-8-3≤4•f(x)-3≤8-3, тобто -11≤4•f(x)-3≤5.
Знайшли E(y)=[-11;5] - область значень функції y=4f(x)-3.
Відповідь: [-11;5] – Г.

Приклад 23.15 У результаті яких послідовних перетворень із графіка функції y=f(x) можна отримати графік функції y=f(2x+6)?

Розв'язування: З графіка функції y=f(x) отримали графік функції y=f(2x) в результаті стиснення удвічі до осі Oy. З графіка функції y=f(2x) отримали графік функції y=f(2(x+3)) в результаті паралельного перенесення на 3 одиниці вліво (відносно осі Ox). Отримали y=f(2x+6).
Відповідь: В.

Приклад 23.16 Областю визначення функції y=f(x) є проміжок [0;2]. Знайти область визначення функції y=f(x/2-4).

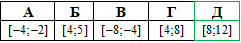
Розв'язування: Функцію y=f(x/2-4) отримують з функції y=f(x) паралельним перенесенням на 4 одиниці вправо та розтягом удвічі від осі Oy. Виконаємо послідовно перетворення
D1(y)=[4;6] - область визначення функції y=f(x-4) (область визначення зсунули на 4 одиниці).
D(y)=[8;12] - область визначення функції y=f(x/2-4) (область визначення розширили удвічі від попередньої).
Отримали варіант Д тестових відповідей.
Відповідь: [8;12] – Д.

Приклад 23.17 Ескіз графіка якої з наведених функцій зображено на рисунку?

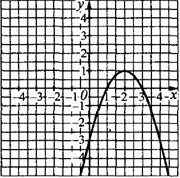
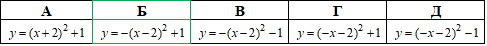
Розв'язування: Візьмемо функцію y=-x^2 (параболу з гілками вниз і вершиною в початку координат, точка (0;0)).
На заданому ескізі графіка вершина параболи знаходиться у точці (2;1), отже графік функції y=-x^2 паралельно перенесли на 2 одиниці вправо (вздовж осі Ox) і на 1 одиницю вгору (вздовж осі Oy).

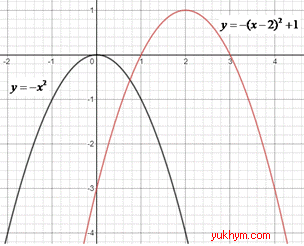
Отримали графік функції y=-(x-2)²+1.
Слідкуйте за тим як змінюються рівняння функцій при відповідних зміщеннях.
Відповідь: y=-(x-2)^2+1 – Б.

Приклад 23.18 Ескіз графіка якої з наведених функцій зображено на рисунку?

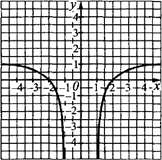
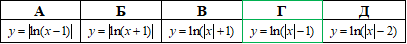
Розв'язування: Оскільки в відповідях фігурують логарифми, то за елементарну функцію над якою будемо виконуватимемо перетворення візьмемо логарифм y=ln(x) (логарифмічна крива, яка перетинає вісь Ox в точці (1;0)).
На заданому ескізі графіка логарифмічна крива перетинає вісь Ox в точці (2;0) і симетрично відображена відносно осі Oy, отже отримаємо паралельне перенесення графіка на 1 одиницю вправо і модуль абсциси x, тобто y=ln(|x|-1).

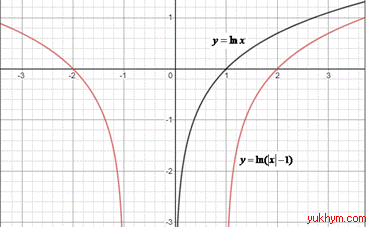
Відповідь: y=ln(|x|-1) – Г.

З наведених прикладів Ви повинні навчитися будувати ескізи графіків функцій за допомогою простих геометричних перетворень, а також за ескізами графіків бачити які дії потрібно виконати, щоб з елементарних функцій прийти до заданого графіка функції.

Попереду Вас чекає біля десятка готових відповідей з підготовки до ЗНО тестів на перетворення графіків функцій.

Паралельне перенесення графіку функції, симетричне відображення, розтяг та стиск

Wed, 01 Apr 2020 15:45:25 +0300

Продовжуємо вивчати основні геометричні перетворення функції і сьогодні розглянемо нові відповіді із ЗНО підготовки з математики на паралельне перенесення графіку функції, симетричне відображення відносно осей, розтяг та стиск до осей графіків функцій. З цього уроку Ви навчитеся складати рівняння функцій за виглядом графіків, а також за графіками прогнозувати, які перетворення графіків простих функцій необхідно виконати.
Для початку трохи повторимо теорію, щоб Ви завжди мали під рукою схеми для розв'язування задач.

Геометричні перетворення графіків функцій

Для побудови графіків функцій Вам необхідно вивчити наступну таблицю з ескізами графіків, щоб знати що робити з функцією у=f(x) :
у=-f(x);у=f(-x);у=f(x)+b;у=f(x+a);у=af(x);у=f(ax);у=f(|x|);у=|f(x)|;|у|=f(x).

Для Вас підготовлено понад 30 готових завдань, тому якщо наступні приклади Вам важкі для розуміння, що і для чого робили, просимо почати вивчати тему геометричних перетворень графіків функцій з уроків, опублікованих раніше. Повірте, що на ЗНО тестах Вас можуть чекати як аналогічні тести, так і значно складніші завдання.

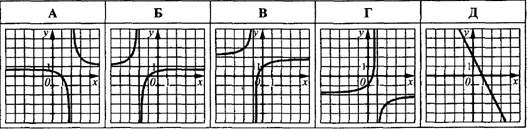
Приклад 23.19 На якому з рисунків зображено графік функції y=(x-1)/(x-2)?

Розв'язування: Зробимо деякі алгебраїчні перетворення виразу:

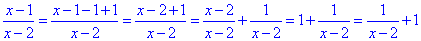
Отримали, y=1/(x-2)+1.
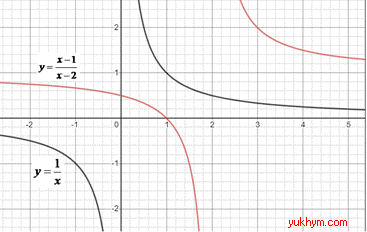
Графік функції y=1/x (гіперболу) зсунули праворуч на 2 одиниці, отримаємо y=1/(x-2).
Графік функції y=1/(x-2) зсунули на 1 одиницю вгору, отримаємо y=1/(x-2)+1.
На рисунку перетворення від першої до кінцевої функції мають вигляд

Порівнюючи робимо висновок, що графік функції y=(x-1)/(x-2) зображений на рисунку А.
Відповідь: А.

Приклад 23.3 Указати формулу функції, графік якої отримують із графіка y=cos(x) у результаті його стискування до осі Ox утричі.

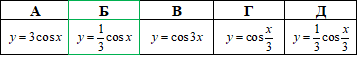
Розв'язування: Графік функції y=c•f(x) можна одержати із графіка функції y=f(x) за допомогою розтягу від осі Ox у c разів, якщо c>1, і за допомогою стиснення до осі Ox у c разів, якщо 0.
Стиснення це зменшення, тому с=1/3. Побудуємо косинусоїду за умовою прикладу.

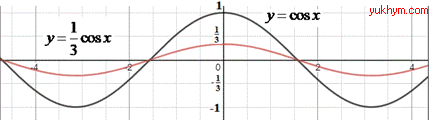
З графіка функції y=cos(x), у результаті його стиснення до осі Ox у тричі, отримаємо функцію y=cos(x)/3.
Відповідь: y=co(x)/3 – Б.
Якщо потрібно розтягнути (0k<1) у k разів графік функції до осі Oy тоді слід використовувати правило 5 таблиці y=f(k•x).

Приклад 23.20 Ескіз графіка якої з наведених функцій зображено на рисунку?

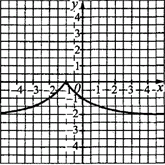
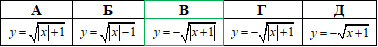
Розв'язування: Візьмемо кореневу функцію y=√x (крива, яка має початок в точці (0;0)). На заданому ескізі графіка функція має лише від’ємні значення (тому y=-√x); симетрично відображена відносно осі Oy (тому y=-√|x|);
має початок у точці (-1;0) (отримаємо паралельним перенесенням графіка y=-√|x| на 1 одиницю ліворуч).

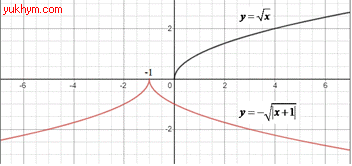
Отримали y=-√|x+1| варант В тестів.
Самостйно розберіться та вивчіть таблицю з основними геометричними перетвореннями, щоб також розуміти, які зміщення на шо впливають та як при цьому змінюються рівняння кривих.
Відповідь: y=-√|x+1| – В.

Приклад 23.29 Установити відповідність між геометричними перетвореннями графіка функції y=cos(x) (1–4) та функціями, одержаних у результаті цих перетворень (А–Д).

1. Графік функції y=cos(x) симетрично відобразили відносно осі Ox

2. Графік функції y=cos(x) симетрично відобразили відносно осі Oy

3. Частину графіка функції y=cos(x), яка лежить вище від осі Ox і на
самій осі, залишили без змін, а частину, яка лежить нижче від осі
Ox, відобразили симетрично відносно цієї осі

4. Першу частину графіка функції y=cos(x), яка лежить праворуч від
осі Oy і на самій осі, залишили без змін, а другу частину замінили
симетричною до першої відносно осі Oy

А. y=|cos(x)|

Б. y=|cos(|x|)|

В. y=cos|x|

Г. y=cos(-x)

Д. y=-cos(x)

Розв'язування: 1. Графік функції y=cos(x) симетрично відобразили відносно осі Ox, отримаємо графік функції y=-cos(x). 1 – Д.

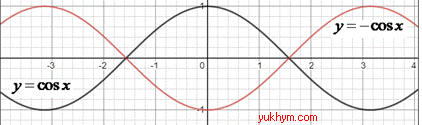
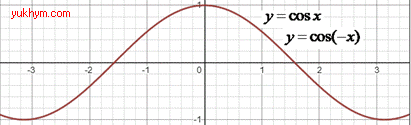
2. Графік функції y=cos(x) симетрично відобразили відносно осі Oy, отримаємо графік функції y=cos(-x). 2 – Г.

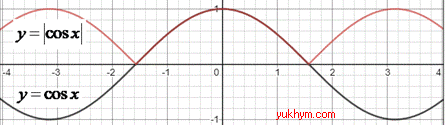
3. Частину графіка функції y=cos(x), яка лежить вище від осі Ox і на самій осі, залишили без змін, а частину, яка лежить нижче від осі Ox, відобразили симетрично відносно цієї осі, отримаємо графік функції y=|cos(x)|. 3 – А.

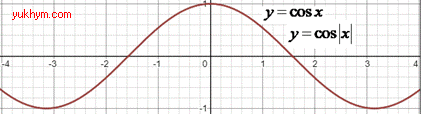
4. Першу частину графіка функції y=cos(x), яка лежить праворуч від осі Oy і на самій осі, залишили без змін, а другу частину замінили симетричною до першої відносно осі Oy, отримаємо графік функції y=cos|x|. 4 – В.

Приклад 23.30 Установити відповідність між графіками функцій (1–4) та їх формулами (А–Д).

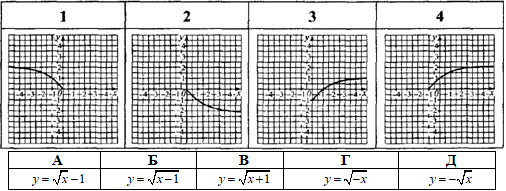
Розв'язування: 1. Графік кореневої функції y=√x симетрично відобразили відносно осі Oy, отримаємо графік функції y=√(-x). 1 – Г.

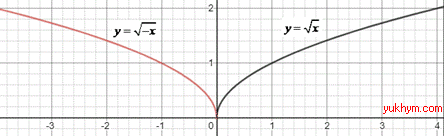
2. Графік кореня y=√x симетрично відобразили відносно осі Ox, отримаємо графік функції y=-√x. 2 – Д.

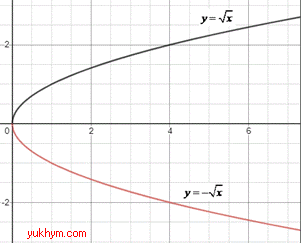
3. Кореневу функції y=√x посунули на 1 одиницю вниз, отримаємо графік функції y=√x-1. 3 – А.

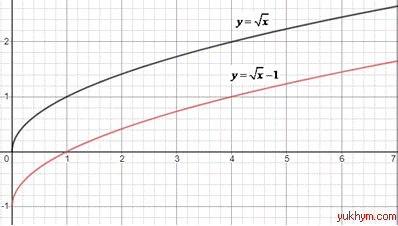
4. Графік функції y=√x посунули на 1 одиницю ліворуч, в результаті отримали графік y=√(x+1). 4 – В.

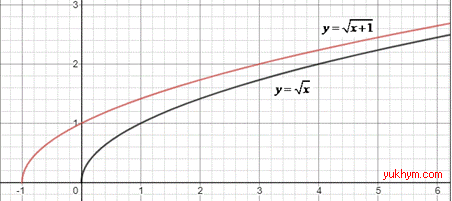
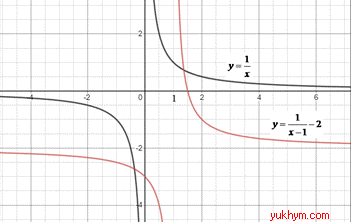
Приклад 23.31 Установити відповідність між графіками функцій (1–4), утворених із графіка функції y=1/x, та їх формулами (А–Д).

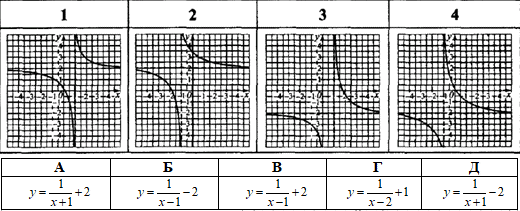
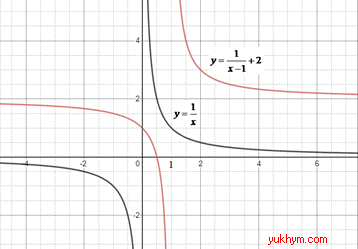
Розв'язування: 1. Графік функції y=1/x паралельно перенесли праворуч на 1 одиницю та паралельно перенесли вгору на 2 одиниці, отримаємо графік функції y=1/(x-1)+2. 1 – В.
На рисунку це має вигляд:

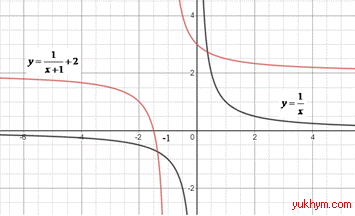
2. Графік функції y=1/x паралельно перенесли ліворуч на 1 одиницю та паралельно перенесли вгору на 2 одиниці, отримаємо графік функції y=1/(x+1)+2. 2 – А.

3. Графік функції y=1/x паралельно перенесли праворуч на 1 одиницю та паралельно перенесли вниз на 2 одиниці, отримаємо графік функції y=1/(x-1)-2. 3 – Б.

4. Графік функції y=1/x паралельно перенесли ліворуч на 1 одиницю та паралельно перенесли вниз на 2 одиниці, отримаємо графік функції y=1/(x+1)-2. 4 – Д.

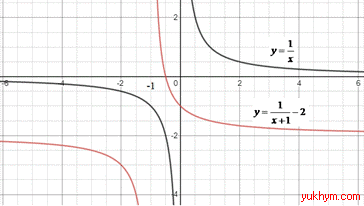
Приклад 23.32 Установити відповідність між ескізами графіків функцій (1–4), утворених із графіка функції y=|x|, та відповідними формулами (А–Д).

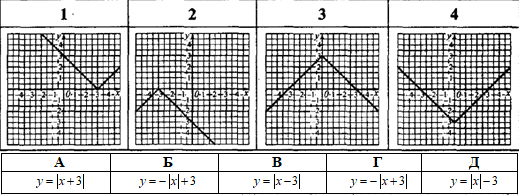
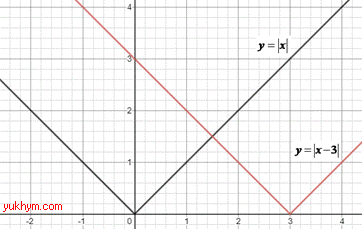
Розв'язування: 1. Графік функції y=|x| паралельно перенесли праворуч на 3 одиниці, отримаємо графік функції
y=|x-3|. 1 – В.

2. Графік функції y=|x| паралельно перенесли ліворуч на 3 одиниці та симетрично відобразили відносно осі Ox, отримаємо графік функції
y=-|x+3| 2 – Г.

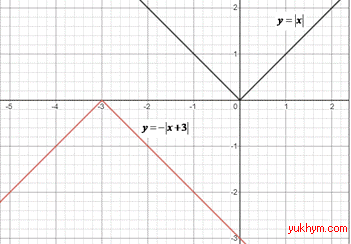
3. Графік функції y=|x| симетрично відобразили відносно осі Ox та паралельно перенесли вгору на 3 одиниці, отримаємо графік функції
y=-|x|+3. 3 – Б.

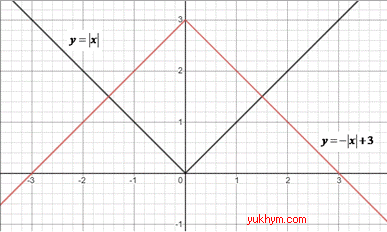
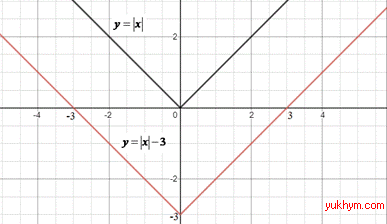
4. Графік функції y=|x| паралельно перенесли вниз на 3 одиниці, отримаємо графік функції
y=|x|-3. 4 – Д.

Наведені приклади на паралельне перенесення графіка функцій вздовж осей, розтяг та стиск, відображення від'ємних або додатних значень в повній мірі повинні підготувати Вас до складання вступних іспитів. Додавайте ресурс в закладки та використовуйте матеріали в шкільній програмі, ЗНО тестах та навчанні у ВУЗах.

Знайти відповідність між функціями та графіками. ЗНО тести

Tue, 31 Mar 2020 19:40:53 +0300

Переходимо до останніх завдань із ЗНО підготовки на геометричні перетворення функції. Теорія та прості приклади на застосування зсуву та паралельного перенесення графіку функцій, його розтягу та стиску розглянуто раніше. Далі на готових відповідях Ви навчитеся за виглядом функцій знаходити їх графіки, області визначення та області значень, самостійно виконувати найпростіші геометричні перетворення. Завдань багато і на щоб розібратися з усіма Вам необхідно уважно переглянути та усвідомити, що від Вас вимагають в умові.

Побудова графіків функцій за допомогою паралельного перенесення, симетричного відображення, розтягу та стиску

Приклад 23.21 Установити відповідність між функціями (1–4) та їх графіками (А–Д).

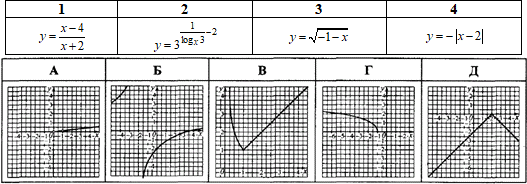
Розв'язування: 1. Перетворимо вихідну формулу функції

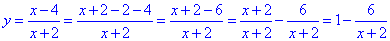
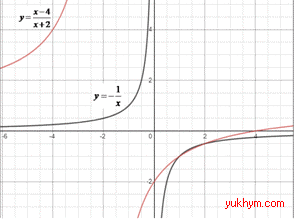
Бачимо, що графік функції y=(x-4)/(x+2) отримують в результаті наступних геометричних перетворень графіка функції y=-1/x (гіпербола з гілками у ІІ у ІV чвертях):
а) паралельним перенесенням на 2 одиниці ліворуч;
б) на 1 одиницю вгору і розтягом у 6 разів, отже 1 - Б.
В результаті отримаємо графік y=(x-4)/(x+2).
Виконуємо побудову елементарної оберненої функції та заданої в умові

2. Враховуючи властивості логарифма, задану функцію перетворимо до вигляду

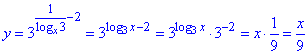
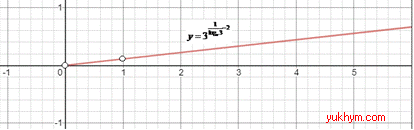
І не забувайте врахувати ОДЗ логарифма при побудові рисунку, тому графіком функції 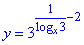є пряма y=x/9 з областю визначення:
x>0 і x≠-1 (за властивістю логарифма log_x3). 2 - А.

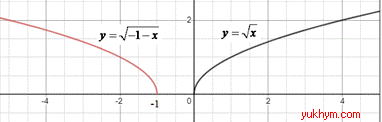
3. Графік кореневої функції y=√(-x-1) отримують в результаті перетворень графіка функції y=√x:
а) симетричним відображенням відносно осі Oy (y=√(-x));
б) паралельним перенесенням на 1 одиниці ліворуч (y=√(-1-x)), отже 3 - Г.
На рисунку нижче наведені обидва графіки.

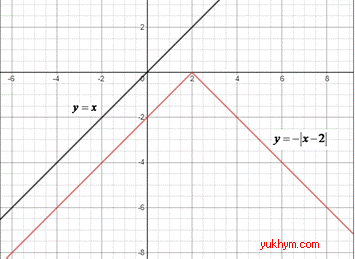
4. Графік модуль функції y=-|x-2| отримують в результаті перетворень графіка функції y=x:
а) симетричним відображенням відносно осі Oy (y=|x|);
б) паралельним перенесенням на 2 одиниці праворуч (y=|x-2|);
в) симетричним відображенням відносно осі Ox усіх додатних y ( y=-|x-2|), отже 4 - Д.
Побудова графіків функцій допомагає краще запам'ятати як змінюються формули функцій при перенесенні та симетричному відображенні. Таких завдань попереду багато і більшість по можливості ми будемо доповнювати ескізами графіків функцій.

Приклад 23.22 Установити відповідність між функціями (1–4) та їх графіками (А–Д).

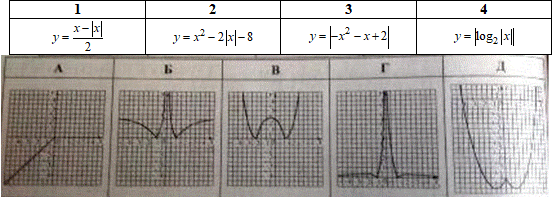
Розв'язування: 1. Графік функції y=(x-|x|)/2 отримують шляхом розкриття модуля:
при x≥0 маємо: y=(x-|x|)/2=0,
при x<0 маємо: y=(x+x)/2=x. 1 - А.

2. Графік функції y=x^2-2|x|-8 отримують методом розкриття модуля:
при x>0 маємо: y=x^2-2x-8 права частина параболи,
при x<0 маємо: y=x^2+2x-8 ліва частина параболи. 2 – Д.

3. Графік функції y=|-x^2-x+2| отримують з графіка y=-x^2-x+2:
y=-x^2-x+2 - парабола з гілками вниз (a=-1<0), з абсцисою у вершині 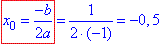та точкою перетину з віссю ординат (0;2).
Частину графіка, яка знаходиться під віссю Ox (від'ємні значення y) симетрично відображають відносно осі абсцис (Ox) і отримуємо графік функції y=|-x^2-x+2|. 3 – В.

4. Графік функції y=|log₂|x|| отримують з графіка y=log₂x:
Спочатку частину графіка, яка знаходиться під віссю Ox симетрично відображаємо відносно осі абсцис і отримуємо графік функції y=|log₂x| (причому частину графіка під віссю абсцис не залишаємо).
Далі отриманий графік симетрично відображають відносно осі ординат і отримуємо графік функції y=|log₂|x||. 4 – Б.
Для підготовки до ЗНО тестувань спробуйте самостійно розв'язати не менше двох подібних завдань.

Приклад 23.23 Установити відповідність між функціями (1–4) та їх графіками (А–Д).

Розв'язування: 1. Графік функції y=|x|in(2x)/x
отримують шляхом розкриття модуля:
при x>0 маємо:

при x<0 маємо:
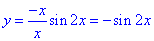1 – Д.

2. Графік функції y=|x+1|+|x-2|+|x-3| отримують методом розкриття модулів:
при x<-1 маємо:
y=-x-1-x+2-x+3=-3x+4 – частина прямої;
при -1 маємо:
y=x+1-x+2-x+3=-x+6 – частина прямої;
при 2 маємо:
y=x+1=x-2-x+3=x+2 – частина прямої;
при x>3 маємо:
y=x+1+x-2+x-3=3x-4 – частина прямої.
В результаті отримаємо ламану, що зображена на рисунку – В.

3. Графік функції y=3^|log₃(x)| отримують методом розкриття модуля і показниково-логарифмічної функції:
при x>1 маємо: 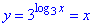– частина прямої;
при 0 маємо: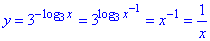
y=1/x частина гіперболи.
З тестових відповідей підходить варіант – Б.
4. Графік функції отримують за властивістю тригонометричних функцій та розкриття модуля:

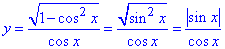
при x∈(0+2πk;π+2πk), k∈Z, маємо:
y=sin(x)/cos(x)=tg(x) - частина лінії тангенса;
при x∈(π+2πk;2π+2πk), k∈Z маємо:
y=-sin(x)/cos(x)=-tg(x) - частина лінії тангенса. 4 – А.
На ЗНО тестах модулі та тригонометричні функції зустрічаються досить часто, тому добре вивчіть їх властивості.

Приклад 23.24 Установити відповідність між рівняннями (1–4) та їх графіками (А–Д).

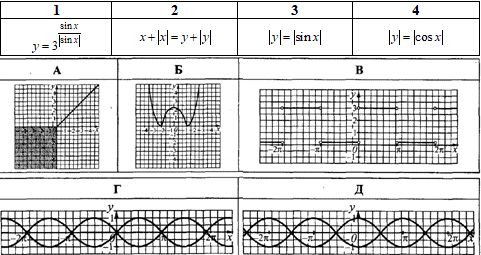
Розв'язування: 1. Графік функції 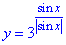отримують розкриттям модуля та властивостей тригонометричних функцій:
при x∈(0+2πk;π+2πk), k∈Z маємо:
y=3^(sin(x)/sin(x))=3 - частина прямої;
при x∈(π+2πk;2π+2πk), k∈Z маємо:
y=3^(-sin(x)/sin(x))=3^(-1)=1/3 - частина прямої. 1 – В.

2. Щоб побудувати графік функції x+|x|=y+|y| розкриваємо модулі для змінних з кожної чверті:
при x>0, y>0 маємо:
x+x=y+y, 2x=2y, x=y - частина прямої;
при x>0, y<0 маємо:
x+x=y-y, 2x=0, x=0 - частина осі Oy;
при x<0, y>0 маємо:
x-x=y+y, 0=2y, y=0 - частина осі Ox;
при x<0, y<0 маємо:
x-x=y-y, 0=0 - частина координатної площини. 2 - А.
Уважно перегляньте як розкривали модулі та повторіть правила.

3. Графік функції |y|=sin(x) отримують розкриваючи модулі для синуса:
при x∈(0+2πk;π+2πk), k∈Z, y>0 маємо:
y=sin(x) - частина синусоїди;
при x∈(0+2πk;π+2πk), k∈Z, y<0, маємо:
-y=sin(x), y=-sin(x) - частина синусоїди;
при x∈(π+2πk;2π+2πk), k∈Z, y>0 маємо:
y=sin(x) - частина синусоїди;
при x∈(π+2πk;2π+2πk), k∈Z, y<0 маємо:
-y=sin(x), y=-sin(x) - частина синусоїди. 3 - Г.

4. Графік функції |y|=|cos(x)| отримують методом розкриття модуля:
при x∈(-Pi/2+2πk;-Pi/2+2πk), k∈Z, y>0 маємо:
y=cos(x) - частина косинусоїди;
при x∈(-Pi/2+2πk;-Pi/2+2πk), k∈Z, y<0 маємо:
-y=cos(x), y=-cos(x) - частина косинусоїди;
при x∈(Pi/2+2πk;3Pi/2+2πk), k∈Z, y>0 маємо:
y=-cos(x) - частина косинусоїди;
при x∈(Pi/2+2πk;3Pi/2+2πk), k∈Z, y<0 маємо:
-y=-cos(x), y=cos(x) - частина косинусоїди. 4 - Д.

Приклад 23.25 Задано функцію y=f(x) з множиною значень [-2;5]. Установити відповідність між функціями (1–4) та їхніми множинами значень (А–Д).

Розв'язування: 1. Графік функції y=f(x)+2 отримали паралельним перенесенням на 2 одиниці вгору графіка функції y=f(x).
Оскільки -2≤f(x)≤5, то -2+2≤f(x)+2≤5+2, тобто 0≤f(x)+2≤7.
E(y)=[0;7] - множина значень функції y=f(x)+2. 1 - Г.
2. Графік функції y=-f(x) отримали симетричним відображенням y=f(x) відносно осі Ox (абсцис).
Оскільки -2≤f(x)≤5, то 2≥f(x) ≥-5, тобто -5≤f(x)≤2.
E(y)=[-5;2] - множина значень функції y=-f(x). 2 - Д.
3. Графік функції y=2f(x) отримали розтягом y=f(x) удвічі відносно осі Ox (абсцис).
Оскільки -2≤f(x)≤5, то -2•2≤2•f(x)≤2•5, тобто -4≤2•f(x)≤10.
E(y)=[-4;10] - множина значень функції y=2f(x). 3 - Б.
4. Графік функції y=|f(x)| отримали симетричним відображенням y=f(x) відносно осі Ox (абсцис) лише ту частину, яка знаходилася під віссю Ox.
Оскільки -2≤f(x)≤5, то -2≤|f(x)|≤5.
E(y)=[0;5] - множина значень функції y=|f(x)|. 4 - А.

Приклад 23.26 Задано функцію y=φ(x) з областю визначення [-4;10]. Установити відповідність між функціями (1–4) та їхніми областями визначення (А–Д).

Розв'язування: 1. Графік функції y=φ(x+4) отримали паралельним перенесенням на 4 одиниці ліворуч (у від’ємному напрямку осі Ox) графіка функції y=φ(x).
Оскільки -4≤x≤10, то -4-4≤x-4≤10-4, тобто -8≤x-4≤6.
D(y)=[-8;6] - область визначення функції y=φ(x+4). 1 - Д.

2. Графік функції y=φ(x-4) отримали паралельним перенесенням на 4 одиниці праворуч (у додатному напрямку осі Ox) графіка функції y=φ(x).
Оскільки -4≤x≤10, то -4+4≤x+4≤10+4, тобто -0≤x+4≤14.
D(y)=[0;14] - область визначення функції y=φ(x+4). 2 - Б.

3. Графік функції y=φ(x)+5 отримали паралельним перенесенням на 5 одиниць вгору (у додатному напрямку осі Oy) графіка функції y=φ(x). Область визначення функцій y=φ(x) і y=φ(x)+5 однакова.
D(y)=[-4;10] - область визначення функції y=φ(x)+5. 3 - А.

4. Графік функції y=φ(x-5)-3 отримали паралельним перенесенням на 5 одиниці праворуч (у додатному напрямку осі Ox) та на 3 одиниці вниз (у від’ємному напрямку осі Oy) графіка функції y=φ(x).
Оскільки -4≤x≤10, то -4+5≤x+5≤10+5, тобто 1≤x+5≤15.
D(y)=[1;15] - область визначення функції y=φ(x-5)-3. 4 - Г.

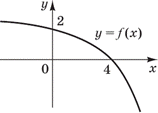
Приклад 23.27 Задано функцію y=h(x) з областю визначення [-2;6]. Установити відповідність між функціями (1–4) та їхніми областями визначення (А–Д).

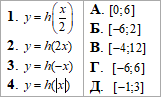
Розв'язування: 1. Графік функції y=h(x/2) розтягом удвічі відносно осі Oy графіка функції y=h(x).
Оскільки -2≤x≤6, то -2•2≤2•x≤2•6, тобто -4≤2•x≤12.
D(y)=[-4;12] – область визначення функції y=h(x/2). 1 - В.

2. Графік функції y=h(2x) стисненням удвічі відносно осі Oy графіка функції y=h(x).
Оскільки -2≤x≤6, то -2/2≤x/2≤6/2, тобто -1≤x/2≤3.
D(y)=[-1;3] – область визначення функції y=h(2x). 2 - Д.

3. Графік функції y=h(-x) отримали симетричним відображенням відносно осі Oy (ординат) графіка функції y=h(x).
Оскільки -2≤x≤6, то 2≤x≤-6, тобто -6≤x≤2.
D(y)=[-6;2] – область визначення функції y=h(-x). 3 - Б.

4. Графік функції y=h(|x|) отримали симетричним відображенням правої частини графіка функції y=h(x) відносно осі Oy (ординат).
Оскільки -2≤x≤6, то -6≤x≤6. Це не зовсім тривіально для Вас, але спробуйте собі уявити, що початкова функція визначена на x∈[-2;6]. Модуль з |x| при x=-6 якраз рівний правому краю проміжку x∈[-2;6].
D(y)=[-6;6] – область визначення функції y=h(|x|). 4 - Г.

Приклад 23.28 На рисунку зображено графік функції y=f(x), спадної на проміжку (-∞;+∞).

Установіть відповідність між функцією (1–4) та точкою перетину її графіка з віссю Ox (А–Д).

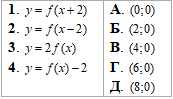
Розв'язування: Графік функції y=f(x) перетинає вісь Ox в точці (4;0).
1. Графік функції y=f(x+2) отримали паралельним перенесенням на 2 одиниці ліворуч (у від’ємному напрямку осі Ox) графіка функції y=f(x).
Тому графік функції y=f(x+2) перетинає вісь Ox в точці (2;0)
(зменшили абсцису точки перетину на 2 одиниці). 1 – Б.

2. Графік функції y=f(x-2) отримали паралельним перенесенням на 2 одиниці праворуч (у додатному напрямку осі Ox) графіка функції y=f(x).
Тому графік функції y=f(x-2) перетинає вісь Ox в точці (6;0)
(збільшили абсцису точки перетину на 2 одиниці). 2 - Г.

3. Графік функції y=2f(x) отримали розтягом y=f(x) удвічі відносно осі Ox (абсцис).
Тому графік функції y=2f(x) перетинає вісь Ox в точці (4;0)
(абсцису точки перетину не змінили). 3 - В.

4. Графік функції y=f(x)-2 отримали паралельним перенесенням на 2 одиниці вниз графіка функції y=f(x).
Тому графік функції y=f(x)-2 перетинає вісь Ox в точці (0;0)
(абсциса і ордината точки перетину співпали у початку координат). 4 - А.

Ви можете використовувати завдання в шкільній програмі, готувати на їх основі презентації, а головне мати уявлення як це легко реалізувати з допомогою простих геометричних перетворень.

Область визначення функції

Wed, 08 Jul 2015 18:22:17 +0300

Областю визначення називають множину значень аргументу x при яких існує значення y=f(x) і позначають D(y) або D(f).
Областю значень називають множину чисел, які приймає функція y=f(x) при проходженні аргументом x всіх визначених значень. Її позначають E(y) або E(f)..Графічно обидві множини добре ілюструє наступний рисунок

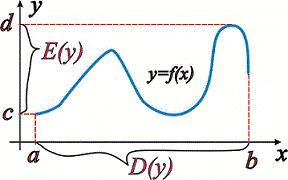
Для схематичної функції розглядувані області приймають значення

Методика знаходження області визначення для всіх функцій одна і та ж: потрібно виявити точки при яких функція не існує, а потім виключити їх з множини дійсних чисел R. В результати отримаємо набір проміжків чи інтервалів, точки, які і утворюють область визначення.

Особливості елементарних функцій

1) Якщо функція має вигляд полінома 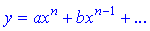, то її областю визначення буде вся дійсна множина 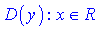або 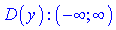. Така функція визначена всюди.

2) Дробово раціональна функція y=f(x)/g(x), де f(x),g(x) – поліноми областю визначення має всі значення аргумента при яких знаменник g(x) не перетворюється в нуль. Тобто розв'язуємо рівняння g(x)=0 і розв'язки, якщо ті існують, вирізаємо з множини дійсних значень. В результаті отримаємо набір інтервалів

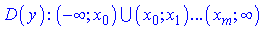
де x₀,...,x_m – корені рівняння g(x)=0.

3) Функція містить корінь парного степеня 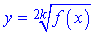. В такому випадку областю визначення будуть точки x, при якому підкоренева функція приймає невід'ємні значення, тобто розв'язки нерівності f(x)>=0.

4) Якщо корінь міститься в знаменнику

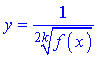
то область визначення визначаємо із строгої нерівності f(x)>0.

5) Якщо в знаменнику маємо корінь непарної степені

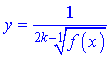
то область визначення знаходимо з умови, що функція не рівна нулеві.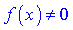

6) Якщо y(x) є логарифмом від іншої функції y=ln(f(x)), то за властивістю логарифма область визначення знаходимо з нерівності f(x)>0. Як правило, це буде інтервал або декілька інтервалів.

7) Експонента y=e^f(x) областю визначення має значення x для яких визначена f(x). Для прикладу, функція y=e^k*x визначена на всій дійсній осі.

8) Прості тригонометричні функції (косинус y=cos(x) та синус y=sin(x) визначені на всій множині дійсних чисел .

9) Тангенси y=tan(x) та котангенси y=cotan(x) областями визначення мають інтервали, які межують точками

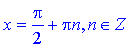
для першої функції та

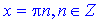
для другої, тобто

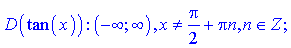
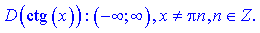
У випадках коли при аргументах є множники y=tan(k*x), точки в яких функція не існує слід визначати з умови

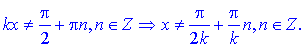
Подібним чином і для котангенса y=cotan(k*x)

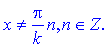
10) Варто зазначити, що обернені тригонометричні функції - арксинус y=arcsin(f(x)) і арккосинус y=arccos(f(x))областями значень мають відрізок [-1; 1]. Для відшукання їх областей визначення необхідно розв'язати подвійну нерівність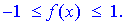
Наприклад, для функції y=arcsin(x+7) маємо нерівність 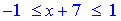з якої отримаємо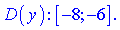
При суперпозиції функцій, тобто коли маємо їх комбінацію, потрібно знаходити область визначення кожної з функцій, після чого перетин знайдених областей.

Приклад 1 Знайти область визначення функції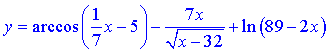

Розв'язання. Область визначення першого доданку знаходимо з нерівності

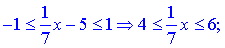
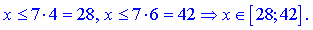
Дробова фунція з оренем у знаменнику та логарифм дадуть наступний вклад

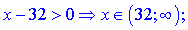
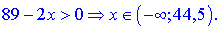
Перетином знайдених множин буде інтервал

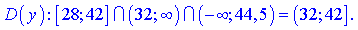
Це і є шукана область визначення.
Побудуємо графік функції в математичному пакеті Maple:
restart;
plot(arccos(x/7-5)-7*x/sqrt(x-32)+ln(89-2*x),x=30..44,-500..0);

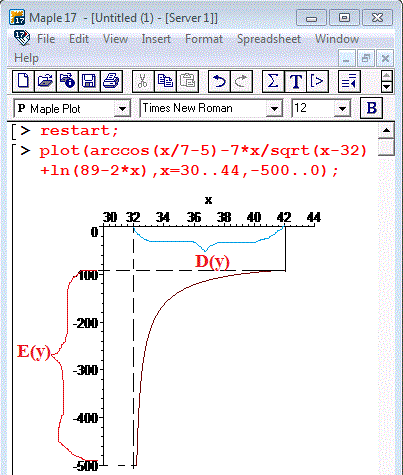
Аналогічним чином виконуть дослідження для функцій двох та більше змінних.

Приклад 2. Знайти і зобразити на малюнку область визначення функції двох змінних z=f(x,y).

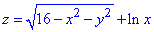
Обчислення: Випишемо ОДЗ кореневої функції та логарифма:

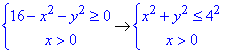
Це і є ті обмеження, які дозволяють побудувати область визначення.
На графіку отримаємо правий півкруг з центром у точці (0;0) і радіусом r=4.

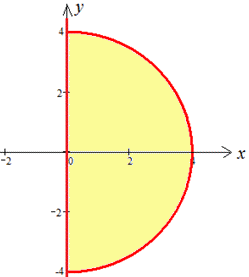
Знаходьте області визначення за наведеною схемою, виключайте всі зайві проміжки та точки та не допускайте помилок. Пам'ятайте, що встановлення областей визначення - це одне з найпростіших завдань при дослідженні функції.