Під складними розуміємо функції виду f(g(q(x))), f(g(x))де f, g, q - елементарні функції. Тобто мова сьогодні піде про складні (вложені) функції, та як знаходити для них області визначення. Схема обчислень базується на знаннях властивостей кореневих, логарифмічних, показникових та тригонометричних функцій. При обчисленнях головне не забути умови, яка обмежує ОДЗ. В цьому Ви зараз переконаєтеся на практиці.
Розділ 22. Елементарні функції та їх властивості
Приклад 22.42 Знайти область визначення функції 
.
У відповідь записати найменше ціле значення аргументу.
Розв'язування: Маємо складну кореневу функцію від логарифма, який в свою чергу містить дробову функцію.
Підкоренева функція, тобто логарифм має приймати невід'ємні значення + дробова функція повинна бути додатно визначена.
Звідси складаємо та розв'язуємо систему двох нерівностей для визначення області визначення:
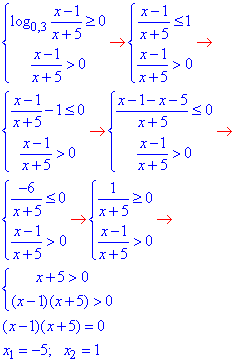
Наносимо знайдені точки на числову вісь і з'яcовуємо спільний перетин усіх нерівностей:
Виписуємо перетин множин, що є областю визначення x∈(1;+ ∞).
Число 2 є найменшим цілим значенням аргументу в області визначення.
Відповідь: 2.
Приклад 22.43 Знайти область визначення функції y=logx+4(908x-x^2). У відповідь записати кількість цілих значень аргументу з області визначення.
Розв'язування: Для логарифма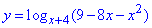 
основа (x+4) повинна бути додатною і не рівною нулю.
Функція під логарифмом повинна приймати додатні значення.
На основі цього складаємо систему трьох нерівностей для знаходження області визначення логарифма
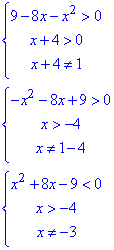
Квадратне рівняння x^2+8x-9=0 обчислюємо за теоремою Вієта
x1=-9, x2=1.
Наносимо точки на числову вісь та визначаємо знаки на інтервалах
Спільними є два інтервали x∈(-4;-3)∪(-3;1).
Запишемо усі цілі значення аргументу з області визначення:
-2; -1; 0.
Усього 3 цілих розв’язки.
Відповідь: 3.
Приклад 22.44 Знайти область визначення функції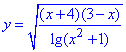 
.
У відповідь записати кількість цілих значень аргументу з області визначення.
Розв'язування: Задана складна коренева функція, аргументом якої є частка добутку (x+4)(3-x) до логарифма десяткового lg(x2+1).
Область визначення знайдемо з нерівностей, які слідують з наступних обмежень на функції:
коренева функція повинна приймати додатні значення або рівні нулю;
знаменник дробу не повинен перетворюватися в нуль lg(x2+1)≠0;
логарифм повинен бути додатно визначений.
Цім висновкам відповідає наступна система трьох нерівностей:
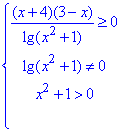
вираз lg(x^2+1)>0 виконується для будь-яких x, тому на першу нерівність системи не впливає і її можна відкинути, враховуючи при цьому другий вираз,
остання нерівність в системі виконується для будь-яких x, тому її можна відкинути, та звести до розгляду наступної
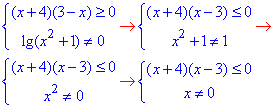
(x+4)(x-3)=0,
x1=-4, x2=3.
З'ясовуємо інтервали знакосталості для знайдених точок
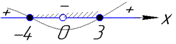
Областю визначення є два проміжки x∈[-4;0)∪(0;3].
Запишемо усі цілі значення аргументу з області визначення:
-4; -3; -2; -1; 1; 2; 3.
Усього 7 цілих розв’язків.
Відповідь: 7.
Приклад 22.45 Знайти область визначення функції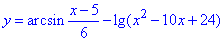 
.
У відповідь записати кількість цілих значень аргументу з області визначення.
Розв'язування: Маємо різницю складного арксинуса та логарифма.
З обмежень на вказані функції складаємо систему нерівностей для ОДЗ:
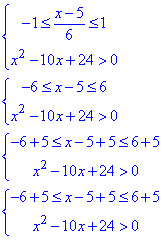
Квадратне рівняння x2-10x+24=0 розв'язуємо за теоремою Вієта отримаємо
x1=4, x2=6.
Щоб не ламати голову, для складних завдань можете будувати розв'язки нерівностей на числовій осі одну під одною. Так легше читати + вищі шанси не помилитися.
Запам'ятайте лише, що результуючими будуть розв'язки обох нерівностей одночасно.
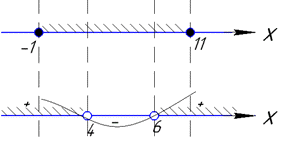
Областю визначення є інтервали x∈[-1;4)∪(6;11].
Запишемо усі цілі значення аргументу з області визначення:
-1; 0; 1; 2; 3; 7; 8; 9; 10; 11.
Усього 10 цілих розв’язків.
Відповідь: 10.
Приклад 22.46 Знайти область визначення функції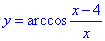 
.
У відповідь записати найменше значення аргументу.
Розв'язування: Складний арккосинус повинен приймати значення, які за модулем не перевищують одиниці.
Крім цього знаменник дробової функції повинен бути відмінним від нуля.
Записуємо ОДЗ та спрощуємо нерівності:
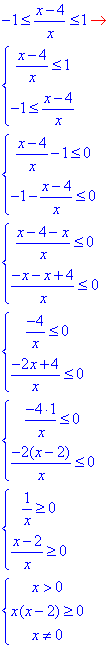
x(x-2)=0,
x1=0, x2=0.
Наносимо точки на числову вісь та визначаємо знаки x(x-2) на інтервалах
Область визначення рівна x∈[2;+∞).
Число 2 є найменшим цілим значенням аргументу з області визначення.
Відповідь: 2.
Приклад 22.47 Знайти область значень функції y=3sin2(x)+2cos2(x).
У відповідь записати кількість цілих значень функції.
Розв'язування: Спростимо суму квадратів синуса та косинуса у правій частині за знаком рівності:
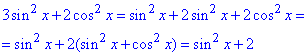
Оскільки областю визначення синуса є інтервал -1≤sin(x)≤1 (за властивістю), то звідси випливає наступне
0≤sin2(x)≤1 (відкинули від’ємні значення).
0+2≤sin2(x)+2≤1+2,
2≤sin2(x)+2≤3.
Завжди аналізуйте від простих функцій до складних, і від вкладених до загальних.
E(y)=[2;3] - область значень функції y=3sin2(x)+2cos2(x).
Запишемо усі цілі значення функції:
2; 3.
Усього 2 цілих значення.
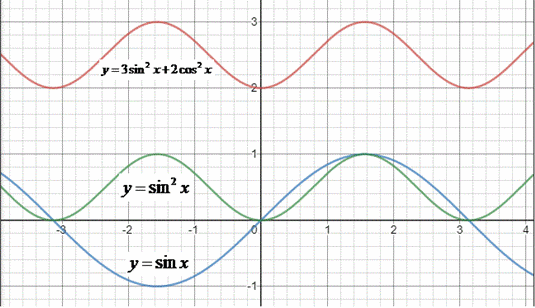
На рисунку позначено графіки функцій:
y=sin(x) (синім кольором);
y=sin2(x) (зеленим кольором);
y=3sin2(x)+2cos2(x) (червоним кольором).
Відповідь: 2.
Приклад 22.48 Знайти найбільше значення функції
.
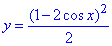Розв'язування: Таку функцію також можна досліджувати, виходячи з елементарних косинуса та квадратичної, що входять сюди.
Оскільки -1≤cos(x)≤1 (за властивістю), то звідси випливає, що
-2≤-2cos(x)≤2,
1-2≤1-2cos(x)≤1+2,
-1≤1-2cos(x)≤3
Далі підносимо до квадрату та ділимо на двійку зі знаменника
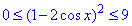(відкинули від’ємні значення),
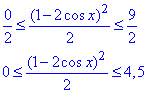
В такий простий для Вас спосіб знайшли E(y)=[0;4,5] - область значень функції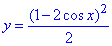
Звідси, число 4,5 є найбільшим значенням функції.
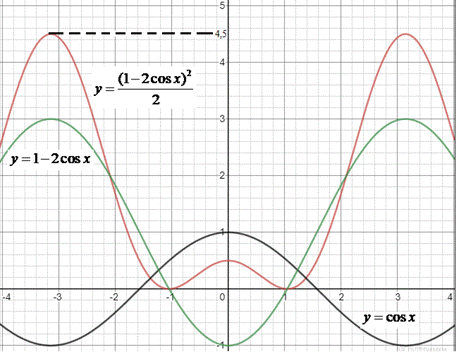
На рисунку позначено графіки функцій: y=cos(x) (чорним кольором);
y=1-2cos(x) (зеленим кольором);
головна 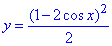(червоним кольором).
Відповідь: 4,5.
Приклад 22.50 Знайти нулі функції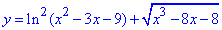 
.
Розв'язування: Нулі функції – це такі значення x (аргументу), при яких y=0.
Складна функція є сумою квадрату логарифма та кореня квадратного від кубічної функції.
Оскільки, їх сума повинна бути рівна нулю, а корінь квадратний завжди або більший або рівний нулю, так само як квадрат логарифма, то нам потрібно знайти так точки при яких обидві функції рівні нулю.
ОДЗ для кореня квадратного: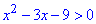 
Основна система має вигляд
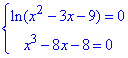
крім цього, розв’язки обох рівнянь мають співпадати.
Розв’яжемо обидва рівняння:
1) ln(x2-3x-9)=0
ln(x2-3x-9)=ln(1)
x2-3x-9=1,
x2-3x-10=0
за теоремою Вієта отримаємо
x1=-2, x2=5.
Обидва корені належать ОДЗ.
2) x3-8x-8=0,
x3+8-8-8x-8=0,
x3+2^3-8x-16=0,
(x+2)(x2-2x+4)-8(x+2)=0,
(x+2)(x2-2x+4-8)=0,
(x+2)(x2-2x-4)=0,
x1=-2,
x2-2x-4=0.
Обчислюємо дискримінант та корені квадратного рівняння
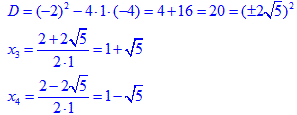
Отже, x=-2 - єдиний спільний корінь обох рівнянь, тому x=-2 - є нулем заданої функції .
Відповідь: -2.
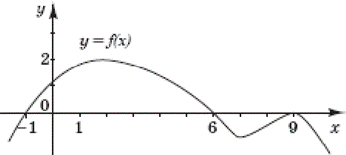
Приклад 22.51 На рисунку зображено графік функції y=f(x), що визначена на проміжку (-∞;∞) і має лише три нулі.
Розв’язати систему нерівностей
.
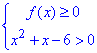У відповідь записати суму всіх цілих розв’язків системи.
Розв'язування:1) За графіком функції y=f(x) знайдемо розв’язки нерівності f(x)≥0 , тобто такі її значення x, при яких крива функції y=f(x) знаходиться над (або на самій) віссю Ox (абсцис, І, ІІ чверть).
З рисунку легко переконатися, що це точки x∈[-1;6]∪{9}.
2) Знайдемо розв’язки нерівності x2+x-6>0.
x2+x-6=0,
за теоремою Вієта отримаємо
x1=-3, x2=2.
Методом інтервалів визначаємо проміжки де виконується нерівність x2+x-6>0.
Отже, x∈(-∞;-3)∪(2;+∞).
3) Знайдемо спільні розв’язки обох нерівностей (тобто системи):
Отже, x∈(2;6]∪{9}.
Випишемо усі цілі розв’язки системи:
3; 4; 5; 6; 9.
Обчислимо їх суму: 3+4+5+6+9=27.
Відповідь: 27.
На цьому завершуємо розділ вивчення властивостей простих функцій, але не закінчуємо готуватись разом до ЗНО з математики.
