Максимумом (мінімумом) функції двох змінних за означенням, це як і для функцій двох змінних максимальне (мінімальне) її значення. На площині це "горби" і "ями", в просторі – те саме тільки двовимірне зображення. Уявити як правило легко, а от для заданої функції знайти точки екстремуму може не кожен.
Схема дослідження функції двох змінних на екстремум
Перше - це перевірити чи виконуються необхідні умови екстремум, а вони наступні – якщо функція має часткові похідні першого порядку і вони рівні нулю то в цих точках функція може мати екстремуми. На практиці реалізація теорії наступна: обчислюємо часткові похідні і прирівнюємо їх до нуля. В результаті потрібно із системи рівнянь
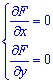
знайти точки (x0; y0) підозрілі на екстремум, їх ще називають стаціонарними.
Щоб встановити чи має місце максимум функції, чи мінімум потрібно обчислити часткові похідні другого порядку (A, B, C) в критичних точках
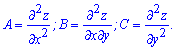
Далі в знайдених точках потрібно обчислити параметр диференціала D
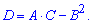
Далі можливі 4 випадки:
- функція має максимум, якщо A<0; D>0
- функція має мінімум, якщо A>0; D>0
- не має екстремуму, якщо D<0
- при D=0 потрібно проводити додатковий аналіз на екстремум.
З аналізу знаків і роблять висновки про точки максимуму та мінімуму функції. Далі підстановкою точок обчислюють сам екстремум функції.
Якщо треба знайти найбільше (найменше) значення функції у замкненій області (трикутник, прямокутник, коло) то ці криві підставляємо у вихідне рівняння та досліджуємо функцію на екстремум по лініях, а також перевіряємо чи стаціонарна точка належить замкненій області. Такий приклад розглянуто в готових контрольних роботах.
Приклади на екстремуми
Приклад 1. Знайти екстремум функції двох змінних
Z=2*x*y-3*x^2-2*y^2
Розв'язок: Щоб знайти критичні точки функції двох змінних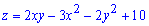 
спершу нам слід обчислити часткові похідні першого порядку
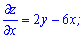
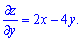
Далі прирівнюємо часткові похідні до нуля і розв'язуємо систему рівнянь
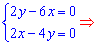
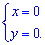
Знайдені значення і є координатами критичної точки. Щоб не досліджувати функцію в околі точки екстремуму, оскільки не маємо графіка функції, встановимо знаки других часткових похідних в цій точці. Обчислюємо похідну другого порядку в критичній точці (0;0)
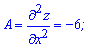
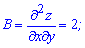
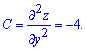
Далі обчислюємо параметр D
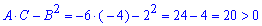
Знак більший нуля, отже в критичній точці (0;0) функція має максимум. Значення рівне вільному члену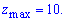 
Графік просторової функції в околі точки екстремуму має вигляд
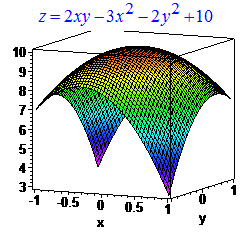
Приклад 1*. Знайти екстремум функції двох змінних z=f(x,y).
z=2x^2+y^2-2y+1
Обчислення: Знайдемо похідні першого порядку заданої функції:
z'x=4x,
z'y=2y-2.
Прирівняємо до нуля отримані вирази та визначимо стаціонарну точку:
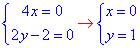
Знайдемо похідні другого порядку в точці (0;1):
z"xx=4,
z"yy=2,
z''xy=0.
За критерієм Сильвестра визначимо знак квадратичної форми:
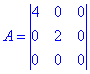
Знаходимо Δ1=2>0, Δ2=8>0, Δ3=0.
Квадратична форма є додатно визначеною, тому в точці (0;1) функція досягає мінімуму. Побудуємо 3D графік в середовищі Мейпл.
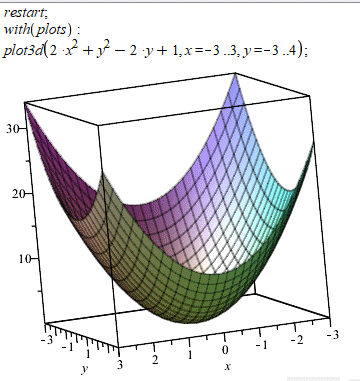
Приклад 2. Знайти точку максимуму або мінімуму заданої функції
Z=4*x-6*y-x^2-3*y^2+5
Розв'язок: За стандартною схемою шукаємо похідні першого порядку
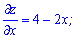
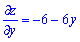
та прирівнюємо їх до нуля. В результаті отримаємо систему рівнянь з якої можемо знайти критичну точку функції
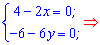
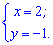
Критична точка відома, її координати (2; -1).
Щоб встановити чи має місце мінімум функції чи максимум знайдемо часткові похідні другого порядку
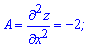
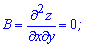
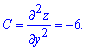
Знаходимо параметр
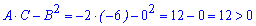
Він додатній, отже в знайденій точці функція досягає максимуму. Обчислимо його значення підстановкою
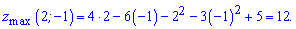
Точка максимуму на графіку матиме вигляд
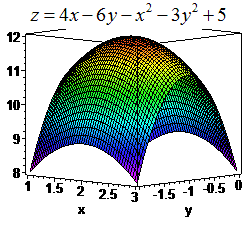
Приклад 3. Дослідити функцію двох змінних на екстремум
Z=3*x^2-x*y+y^2-7*x-8*y+2
Розв'язок: Обчислюємо часткові похідні першого порядку функції
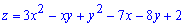
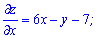
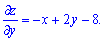
Прирівнюємо похідні до нуля і розв'язуємо систему рівнянь
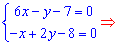
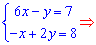
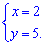
Критична точка має координати (2; 5). Для з'ясування характеру точки екстремуму знайдемо похідні другого порядку в критичній точці
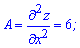
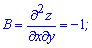
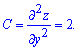
Обчислюємо параметр
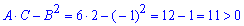
Знак A, D додатний, значить в точці (2; 5) дана функція має мінімум, обчислюємо мінімальне значення
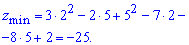
Графік функції двох змінних наведено нижче
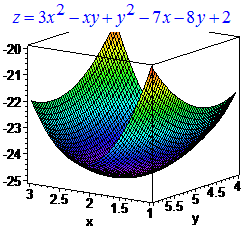
Приклад 4. Знайти екстремум функції двох змінних
Z=2*x^2-3*y^2+4*x+6*y+5
Розв'язок: Знайдемо критичні точки функції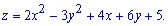 
Обчислюємо часткові похідні
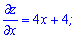
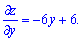
та прирівнюємо їх до нуля. В результаті дістанемо систему рівнянь для знаходження точки екстремуму
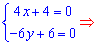
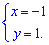
Знайдемо похідну другого порядку в стаціонарній точці (-1; 1)
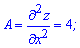
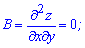
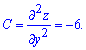
Обчислюємо параметр D
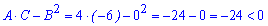
Знаки A>0,D<0, отже в точці (-1; 1) функція не досягає екстремуму. Це є точка перегину просторової функції. На графіку це має вигляд
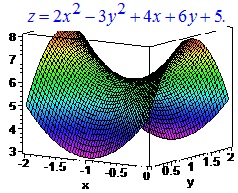
Приклад 5. Дослідити функцію на екстремум
Z=x^3+y^3-15*x*y+120.
Розв'язок: Повторюємо всі пункти методики знаходження екстремумів.
Обчислюємо часткові похідні функції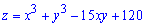 
першого порядку
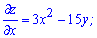
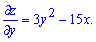
Прирівнюємо їх до нуля та розв'язуємо
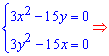
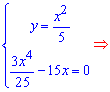
Звідси отримуємо дві підозрілі на екстремум точки
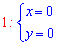
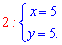
Далі знаходимо похідні другого порядку в критичних точках (0; 0) і (5; 5)
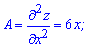
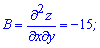
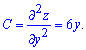
Характер першої критичної точки:
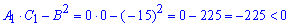
В точці (0; 0) дана функція не має ні максимуму, ні мінімуму.
Характер другої критичної точки:
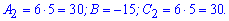
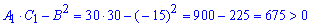
За ознаками екстремуму дана функція має мінімум, а саме
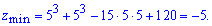
Аналіз функції двох змінних в Мейпл
Наведемо алгоритми аналізу функції та побудови графіків в математичному пакеті Maple. Фрагмент коду дещо простіший ніж обчислення вручну. Спершу потрібно занулити всі змінні і підключити бібліотеку для побудови 3D графіків
>restart;with(plots):
Далі вводимо саме рівняння просторової функції
> Z=x^3+y^3-15*x*y+120;
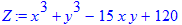Обчислюємо часткові похідні
> diff(Z,x)=0;diff(Z,y)=0;
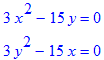Другі похідні можна знайти повторним диференціюванням
> A:=diff(Z,x,x);C:=diff(Z,y,y);B:=diff(Z,x,y);
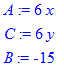Знаходимо розв'язки системи рівянянь командою solve
> solve({diff(Z,x)=0,diff(Z,y)=0},{x,y});
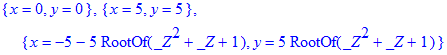Далі будуємо графіки функції за допомогою команди plot3d(F,x=a..b,y=c..d) .Тут всі позначення повинні бути Вам зрозумілі
> plot3d(Z, x= -1..1, y=-1..1);
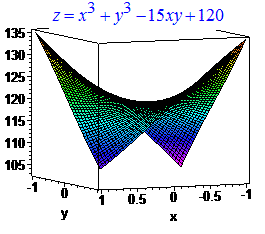> plot3d(Z, x= 4..6, y=4..6);
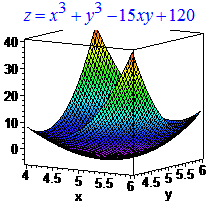В мейплі немає потреби аналізувати другі похідні, оскільки можемо побудувати графік і візуально перевірити чи маємо максимум, чи мінімум, а можливо і перегини, як в останньому прикладі. Завантажити математичний пакет Maple Ви можете з офіційного сайту або пошукати інсталяційний пакет у мережі інтернет. Приклади наведено у пакеті Maple 17.
Подібно до наведеного виглядає аналіз на екстремуми,якщо задані тригонометричні чи показникові функції. Все зводиться до рівнянь на похідні і обчислень, які Ви часто виконуєте на заняттях.
Якщо не можете виконати аналіз на екстремум самостійно, тоді замовляйте розв'язання задач, контрольних у нас!
