Відшукання максимумів та мінімумів – одне з поширених завдань при дослідженнях функцій.
Неперервна на відрізку [a;b] функція y=f(x) набуває своїх найбільшого та найменшого значень, або в критичних точках (у точках, в яких похідна перетворюється в нуль чи не існує), що належать досліджуваному проміжку, або на його кінцях x=a, x=b.
На практиці знаходження максимумів та мінімумів подібне до відшукання локального екстремуму, тільки добавляються краї проміжку. Можливі випадки коли максимуми та мінімуми функцій знаходяться в точках локального екстремуму, а можливі - на краях відрізку.
Розглянемо ряд прикладів, щоб ознайомити Вас з методикою дослідження.
-----------------------------------
Приклади. Визначити найбільше та найменше значення фунції на проміжку.
Збірник В.Ю. Клепко, В.Л. Голець "Вища математика в прикладах і задачах".
1. (4.55.б)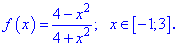 
Розв'язування: Функція визначена на всій множині дійсних чисел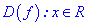 
. Хоча вона і дробова, проте знаменник ніде не перетворюється в нуль.
Знайдемо похідну функції
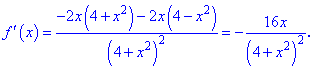
Прирівняємо її до нуля та визначимо критичні точки
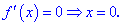
Перевіримо знак похідної зліва та справа від знайденої точки
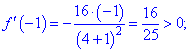
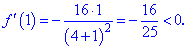
Похідна при переході через точку x=0 змінює знак з додатного "+" на від'ємний "-", отже вона є точкою локального максимуму.
Знайдемо значення функції в точці x=0
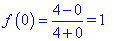
та на краях відрізку
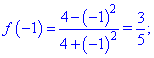
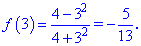
Таким чином функція досягає максимуму в точці локального екстремуму fmax(0)=1, а мінімуму на одному з країв відрізку fmin(3)=-5/13.
Для повного представлення, що ми досліджуємо, побудуємо графік функції на інтервалі в математичному пакеті Мaple:
restart; with(plots);
plot((4-x^2)/(4+x^2),x=-2..4);
В результаті отримаємо графік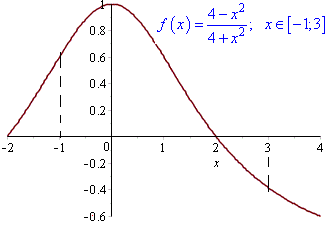
Дослідження на максимуми та мнімуми теж можна проводити в Мaple, але проце поговоримо на іншому уроці.
2. (4.55.д)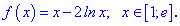 
Розв'язування: На заданому проміжку функція визначена всюди, обчислимо її похідну
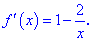
З умови рівності похідної нулю знаходимо критичну точку
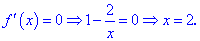
Задана точка належить розглянутому відрізку. Знайдемо значення функції в критичній точці та на краях
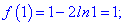
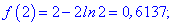
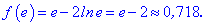
Функція набуває максимуму і мінімуму в точках
fmax(1)=1, fmin(2)=0,6137.
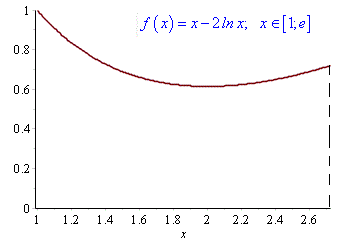
Побудуємо графік функції в Мaple
plot(x-2*ln(x), x = 1 .. exp(1), 0 .. 1);
3. (4.55.є)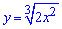 
Розв'язування: Функція визначена для всіх значень аргумента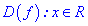 
.
Знайдемо похідну
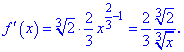
З виразу бачимо, що похідна відмінна від нуля на проміжку визначення, однак в точці x=0 вона не існує.
Обчислимо значення функції в підозрілих на екстремум точках
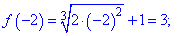
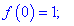
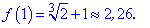
Найбільше значення функція приймає в точці fmax(-2)=3 , а найменше значення в критичній точці fmin(0)=1.
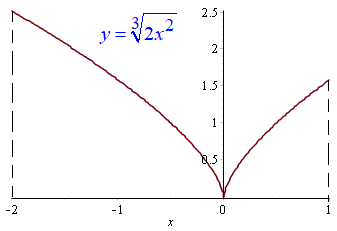
Графік досліджуваної функції наведено нижче
plot((2*abs(x))^(2/3), x = -2 .. 1);
Наведемо розв'язки задач із збірника Дубовик В.П., Юрик І.І. "Вища математика" .
4. (5.770)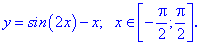 
Розв'язування: Синус функція визначена всюди, тому приступаємо до знаходження похідної
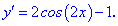
Прирівняємо її до нуля та знайдемо критичні точки
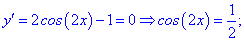
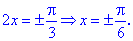
Знайдемо значення функції у всіх підозрілих на екстремум точках
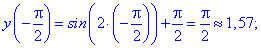
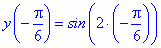
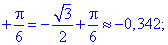
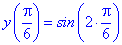
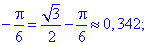
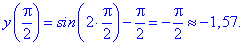
З отриманих значень випливає, що функція приймає максимум та мінімум на краях відрізку
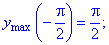
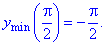
Побудуємо графік функції
plot(sin(2*x)-x, x = -(1/2)*Pi .. (1/2)*Pi);
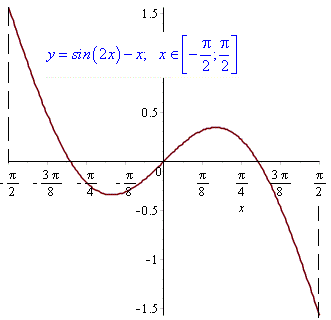
5. (5.771)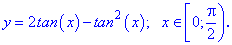 
Розв'язування: На заданому інтервалі функція визначена, тому переходимо до диференціювання
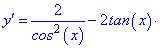
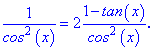
Прирівнявши до нуля похідну отримаємо
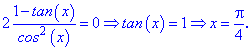
Іншу критичну точку знайдемо з умови, що похідна не існує
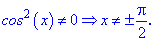
Одна співпадає з початком відрізку. Обчислимо значення функції на краях відрізку та в критичних точках
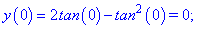
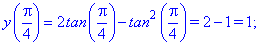
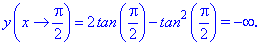
Таким чином функція приймає максимальне значення в критичній точці, а мінімальне на кінці відрізку
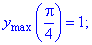
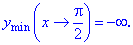
Виконаємо побудову графіка функції в Maple
plot(2*tan(x)-tan(x)^2, x = 0 .. (1/2)*Pi);
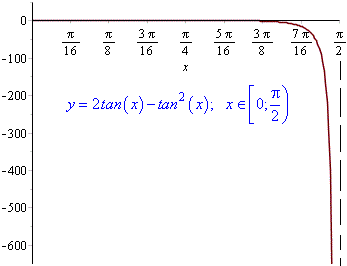
З наведених розв'язків можна зробити висновки, що головним в обчисленні є знання функцій та вміння диференціювати. Все решта зводиться до відшукання значень функцій в точках та аналізу результатів. Вивчайте властивості елементарних функцій, правила знаходження похідних, це Вам стане в нагоді при знаходженні екстремумів.
