Приклади на періодичність функцій, основний період

Періодичність тригонометричних функцій не складна, якщо розглядаємо класичні тригонометричні функції sin(x), cos(x), tg(x), ctg(x). Cинус та косинус періодом мають 2Pi, тангенс та котангенс – Pi. Проблеми у Вас починаються, коли потрібно знайти перод tg(3x+5), sin(x/2)+cos(x/3), ctg(Pi·x/5) та подібних комбінацій функцій. Щоб навчитися визначати основний період функцій та знати формули за якими можна обчислити період суми синусів, чи інших комбінацій тригонометричних функцій Вам потрібно розібратися з готовими відповідями до прикладів, що відповідають підготовці до ЗНО тестів.

Розділ 22. Елементарні функції та їх властивості

Приклад 22.19 Вказати функцію, в якої основний період дорівнює Pi.

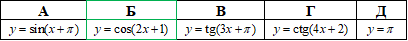
Розв'язування: Найменше додатне число T0, яке є періодом функції (тобто f(x±T0)=f(x)) називають найменшим додатним періодом, або основним періодом цієї функції. Знайдемо основні періоди заданих функцій:
y=sin(x+Pi), тому T0=2Pi;
Далі будьте уважні, особливо коли складаємо прості рівняння на період.
y=cos(2•x+1), отже 2•T0=2Pi, звідси T0=Pi;
y=tg(3x+Pi), отже 3•T0=Pi, звідси T0=Pi/3;
y=ctg(4x+2), отже 4•T0=Pi, звідси T0=Pi/4;
y=Pi - не є періодичною функцією.
Відповідь: y=cos(2x+1) – Б.

Приклад 22.20 Знайти основний період функції y=cos²(6x).

Розв'язування:Понизимо степінь косинуса
,
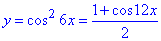тоді період рівний 12•T0=2Pi, звідси T0=2Pi/12=Pi/6.
Тут використали формулу пониження степеня:
.
Відповідь: Pi/6 – Д.

Приклад 22.21 Знайти основний період функції .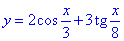

Розв'язування:Тут маємо суму двох косинусів, знаходимо почергово їх періоди y₁=2cos(x/3), отже T₁/3=2Pi, звідси T₁=6Pi;
y₂=3tg(x/8), отже T₂/8=Pi, звідси T₂=8Pi.
Основний період заданої суми косинусів рівний найменшому спільному кратному (НСК) між T₁=6Pi і T₂=8Pi,
T₀=НСК(6Pi;8Pi)=24Pi - основний період функції y=2cos(x/3)+3tg(x/8).
Відповідь: 24Pi – В.

Приклад 22.34 Установити відповідність між функціями (1–4) та їх найменшими додатними періодами (А–Д).

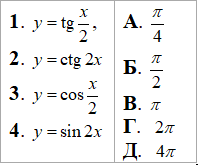
Розв'язування: Задані тригонометричні функції з певними множниками при аргументі. Пам'ятайте, що період класичного синуса та косинуса рівний 2Pi, а період T₀ тангенса та котангенса рівний π. Це необхідно знати, щоб досить швидко виконати наступні обчислення додатних періодів.
1. y=tg(x/2), 1/2T₀=π , звідси T₀=2π. 1 - Г.
2. y=ctg(2x), 2T₀=π, звідси T₀=π/2. 2 - Б.
3. y=cos(x/2), 1/2T₀=2π, звідси T₀=4π. 3 - Д.
4. y=sin(2x), 2T₀=2π, звідси T₀=π. 4 - В.

Приклад 22.49 Знайти найменший додатний період T₀ функції .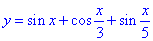
У відповідь записати значення T₀:π.
Розв'язування: y₁=sin(x), отже T₁=2π;
y₂=cos(x/3), отже T₂/3=2π, звідси T2=6π;
y₃=sin(x/5), отже T₃/5=2π, звідси T3=6π.

Знайдемо НСК (найменше спільне кратне) між T₁=2π, T₂=6π і T₃=6π, отже
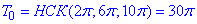- основний (найменший додатний) період функції y=sin(x)+cos(x/3)+sin(x/5).
Обчислюємо T₀:π =30.
Відповідь: 30.

Особливої уваги заслуговують завдання з параметром, тому будьте уважними при їх розв'язуванні.

Приклад 22.53 За яких значень параметра a число π є періодом функції f(x)=cos(x)/(a+sin(x))
?
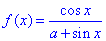Розв'язування: Функція f(x) періодична, якщо f(x)=f(x+T), де T є періодом функції.
Отже,
.
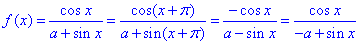Отримали,

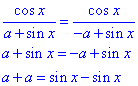
2a=0
a=0.
При a=0 функція з параметром f(x)=cos(x)/(a+sin(x)) перетворюється в котангенс
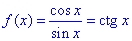з періодом T₀=π.
Відповідь: 0.

Приклад 22.54 Для функції y=2sin(πx+3)-7 знайти:
1. основний період;
2. найбільше значення.
Розв'язування: Знайдемо основний період заданої функції y=2sin(πx+3)-7:
πT₀=2π, звідси T₀=2.
Знайдемо множину значень заданої функції y=2sin(πx+3)-7:
-1≤sin(πx+3)≤1
(за властивістю функції синуса),
-2≤2sin(πx+3)≤2,
-2-7≤2sin(πx+3)-7≤2-7,
-9≤2sin(πx+3)-7≤-5 .
Отже, E(y)=[-9;-5] - множина значень заданої функції.
Звідси, y_max=-5 - найбільше значення функції.
Відповідь: 2; -5.
Повторіть обчислення аналогічних завдань самостійно та перевірте, чи добре Ви запам'ятали схеми обчислень.