Властивості параболи y=ax^2+bx+c необхідно добре знати, щоб правильно будувати графіки парабол, швидко знаходити вершину параболи, а також для встановлення знаків коефіцієнтів a,b,c за ескізами графіків. Такі завдання зустрічаються як в шкільній практиці, так і при здачі вступних тестів, дал на перших курсах ВУЗів. Підготовлені далі готові відповіді взяті із збірника для ЗНО підготовки з математики. Почнемо розгляд від найпростіших завдань і далі до ескізів та завдань з параметром.
Приклад 22.6 Знайти множину значень функції y=-x2+4x-5.
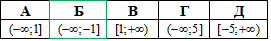
Розв'язування: Множину значень, яких набуває залежна змінна (функція), називають областю значень функції E(y).
Побудуємо для повного уявлення графік.
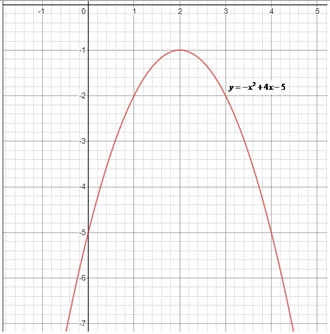
y=-x^2+4x-5 - парабола (y=a•x^2+b•x+c) з гілками вниз (a=-1<0), тому її вершина є найбільшим значенням заданої функції, найменшого значення не існує (тобто ymin=-∞).
Отже, знайдемо координати вершини параболи:
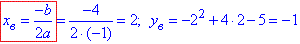
Отримали (2;-1).
У вершині досягається максимальне значення, тому E(y)=(- ∞;-1] - множина значень заданої функції.
Відповідь: (- ∞;-1] – Б.
Приклад 22.7 Обчислити відстань від початку координат до вершини параболи y=-x2+10x-13.
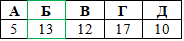
Розв'язування: Рівняння параболи має вигляд:
y=a•x^2+b•x+c.
За умовою y=-1•x^2+10•x+(-13) (a=-1, b=10, c=-13).
Знайдемо координати її вершини:
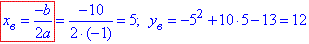
Отримали A(5;12). Наведемо рисунок заданої параболи
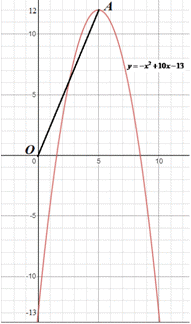
Початок координат знаходиться у точці O(0;0).
Знайдемо відстань між точками O(0;0) і A(5;12) за формулою:
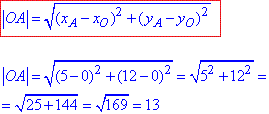
Відповідь: 13 – Б.
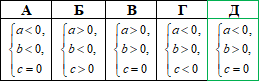
Приклад 22.17 На рисунку зображено ескіз графіка функції y=a•x2+bx+c.
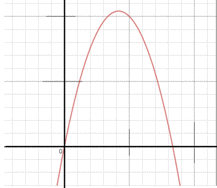
Указати правильне твердження щодо коефіцієнтів a, b, c.
Розв'язування: Графіком функції y=a•x2+bx+c є парабола. У параболи гілки напрямлені вниз, тому a<0.
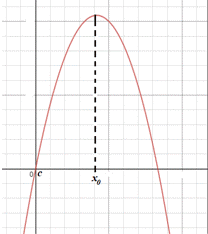
З формули вершини параболи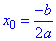 
випливає:
оскільки x0>0 і a<0, то b>0). Параметр c вказує на ординату перетину параболи з віссю Oy.
На ескізі графіка c=0 (задана парабола проходить через початок координат).
Остаточні коефіцієнти параболи a<0, b>0, c=0.
Відповідь: { a<0, b>0 , c=0}– Д.
Приклад 22.18 За яких значень a парабола y=9x^2-12x+35a має з віссю абсцис дві точки перетину?
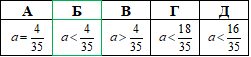
Розв'язування: Парабола y=9x2-12x+35a має з віссю абсцис дві точки перетину, якщо дискримінант D відповідного квадратного рівняння 9x^2-12x+35a=0 більший нуля (D>0).
Обчислимо дискримінант рівняння
звідси складемо нерівність для знаходження параметра
144-1260a>0,
-1260a>-144,
a<144/1260, або a<4/35.
Відповідь: a<4/35 – Б.
Приклад 22.37 Дано квадратичну функцію y=ax^2+bx+c. Установити відповідність між ескізами графіків функцій (1–4) та знаками коефіцієнтів a, b й c (А–Д).
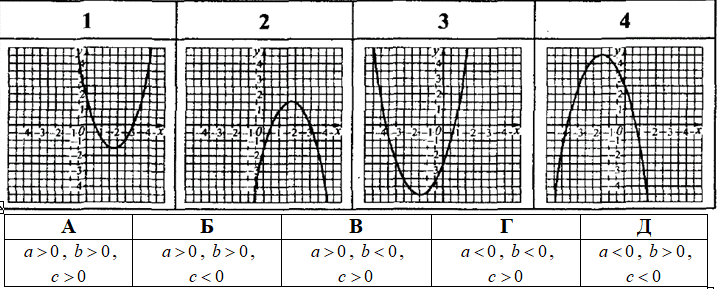
Розв'язування: Графіками заданих функцій y=ax^2+bx+c є параболи.
Якщо гілки напрямлені вгору, то a>0, якщо вниз, то a<0.
З формули вершини параболи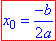 
виводимо значення другого параметра:
Звідси слідує, якщо a і x0 (абсциса вершини параболи) різних знаків, то b>0;
якщо a і x0 мають однакові знаки, то b<0.
Параметр c вказує на ординату перетину параболи з віссю Oy (Значення по y при x=0).
1. a>0, (x0>0), b<0 і c>0. 1 – В.
2. a<0, (x0>0), b>0 і c<0. 2 – Д.
3. a>0, (x0<0), b>0 і c<0. 3 – Б.
4. a<0, (x0<0), b<0 і c>0. 4 – Г.
Приклад 22.38 Установити відповідність між функціями (1–4) та проміжками їх зростання (А–Д).
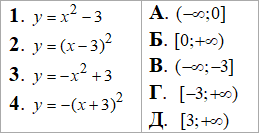
Розв'язування: Графіками заданих функцій є параболи з абсцисами вершини x0, які є зміщені відносно «головної» параболи y=x2 (або y=-x2, якщо гілки йдуть вниз).
Якщо гілки параболи напрямлені вгору, то проміжок зростання: [x0;+∞);
якщо гілки параболи напрямлені вниз, то проміжок зростання функції: (-∞;x0].
Для наочності перегляньте рисунок з графіками парабол, що досліджуємо.
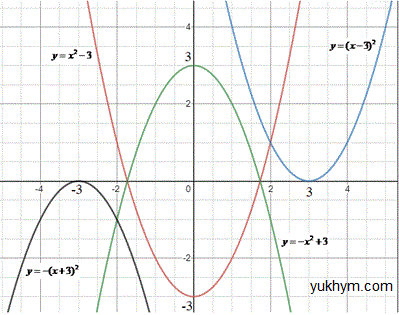
1. y=x2-3 - парабола з гілками вгору і зміщена на 3 одиниці вниз (відносно y=x2), тому x0=0, проміжок зростання: [0;+∞) 1 - Б.
На графіку задана парабола позначена червоним кольором.
2. y=(x-3)2 - парабола з гілками вгору і зміщена на 3 одиниці вправо (відносно y=x^2), тому x0=3, проміжок зростання: [3;+∞) 2 - Д.
На графіку задана парабола позначена синім кольором.
3. y=-x^2+3 - парабола з гілками вниз і зміщена на 3 одиниці вгору (відносно y=-x2), тому x0=0, проміжок зростання: (-∞;0] 3 - А.
На графіку задана парабола позначена зеленим кольором.
4. y=-(x+3)2 - парабола з гілками вниз і зміщена на 3 одиниці вліво (відносно y=-x2), тому x0=-3, проміжок зростання: (-∞;-3] 4 - В.
На графіку задана парабола позначена чорним кольором.
Готових завдань на параболи в нас досить багато, на будь-яку складність.
Залишайтесь з нами, вивчайте математику та діліться посиланням на сайт з друзями!
- Вас може зацікавити:
- Приклади на область визначення та властивості елементарних функцій
- Розвязування задач на найбільше та найменше значення функції на відрізку
- Приклади на множину значень функції, знаходження функції за ескізом
- Критичні точки на графіку функції
- Геометричні перетворення графіків функцій. ЗНО підготовка
