Схема повного дослідження функції детально розписана в попередніх уроках. Тут ми продовжуємо аналізувати можливі на практиці приклади, пов'язані з визначенням інтервалів монотонності, екстремумів, перегинів графіка функцій та знаходження асимптот. Матеріал в першу чергу буде корисний студентам заочникам, оскільки все приходиться освоювати самостійно, а якісних матеріалів в інтернеті не так і багато.
ЗАВДАННЯ 1 Знайти проміжки монотонності й екстремуми функції:
f(x)=x/ln(x).
Розв'язання: 1) Область допустимих значень (ОДЗ):
Всі точки де визначений логарифм, окрім значення де він рівний нулю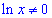 
, звідси "ікс" більший одиниці 
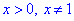, тобто дійсна вісь розбита на інтервали одиницею
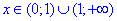
2) Знайдемо похідну заданої функції: f'(x)=(ln(x)-1)/ln2(x)
3) Знайдемо критичні точки: f'(x)=0
(ln(x)-1)/ln2(x),
ln(x)-1=0,
ln(x)=1 звідси x=e - критична точка.
4) Запишемо проміжки монотонності й екстремум функції (інтервали де похідна або додатна, або від'ємна):
Перевіримо знак похідної, для цього усно (Ви можете перевірити) підставимо точки з інтервалів у рівняння похідної.
Таким чином на двох інтервалах (0;1)U(1;e) – функція спадає;
від експоненти до нескінченності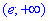
– функція зростає;
Результати дослідження функції записуємо в таблицю
Така систематизація дозволяє краще бачити, що за функція задана, та як будувати.
Значення функції при аргументі рівному експоненті
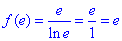
(e;e) (мінімум) – точка екстремуму функції.
В нулі границя функції рівна одиниці, наведена функція має наслідок з важливої границі.
Далі Вас вчать протабулювати функцію в кількох точках з області визначення та в зошиті в клітинку виконати побудову графіка функції. Для шкільного навчання це підходить і це правильно, Ви вчитеся старанно виконувати рисунки, працювати з олівцем та лінійкою.
Але я Вам таких рисунків тут не приведу, дальше Вас чекає навчання у ВУЗах та робота на фірмах, де геть інші вимоги до оформлення результатів і про це повинні говорити не викладач студентам, а вчителі школярам, готуючи останнх до реалій життя.
Тому наведемо Вам графік заданої функції зроблений в математичному пакеті Maple.
Для цього Вам знадобиться всього кілька рядків коду
> restart: with(plots):
> q1:=plot(x/ln(x),x=0..0.999,-30..0,thickness=2,color=blue):
> q2:=plot(x/ln(x),x=1.01..3,0..30,thickness=2,color=blue):
> q3:=plot([[1,-30],[1,30]],thickness=1,color=red):
> display(q1,q2,q3);
щоб побудувати графік функції разом з вертикальною асимптотою
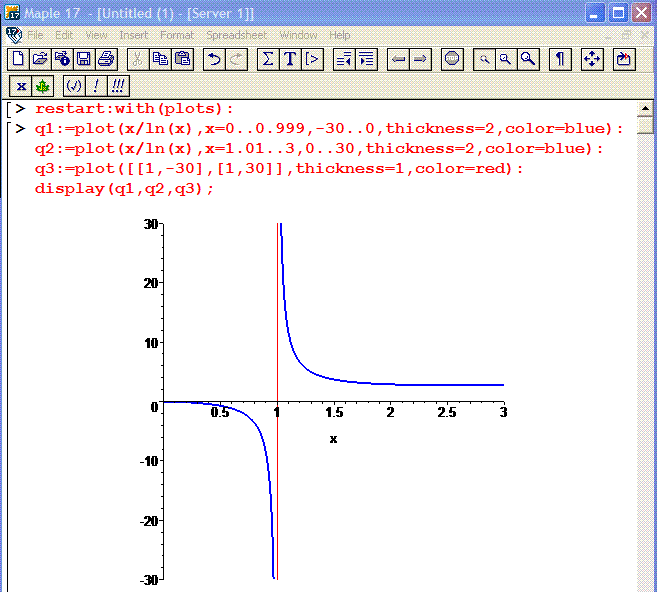
Тут права сторона дещо обрізана, оскільки від експоненти =2,71828 функція починає зростати.
Тому права частина містить фрагмент, що включає локальний мінімум функції. Щоб побачити правіше графік функції, достатньо в q2 змінити межі x=1.01..10.
Можете самостійно поекспериментувати та з'ясувати, що за що відповідає.
ЗАВДАННЯ 2 Виконати повне дослідження функції та побудувати її графік
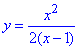
Розв'язання:
А) Область визначення функції ОДЗ:
В дробовій функції знаменник повинен приймати додатні значення. З цієї умови маємо
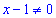, тобто маємо два інтервали визначеності функції
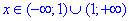
Б) Нулі функції:
при x=0,y=0;
при y=0, x=0.
Графік заданої функції перетинає осі координат в точці (0;0).
В) Дослідження на парність:
Підставимо від'ємний аргумент та перевіримо, що отримаємо
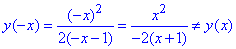
функція не є парною, ні непарна .
Г) Знайдемо критичні точки функції:
Похідна функції за правилом частки рівна:
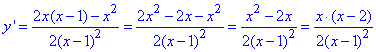
Прирівнявши похідну до нуля y'=0 знаходимо точки, підозрілі на екстремум
x(x-2)=0,
звідси x1=0 і x2=2 - критичні точки.
Д) Інтервали зростання та спадання, точки max і min функції:
Вибираємо довільні точки з області визначення, що лежать між критичними точками та перевіряємо знак похідної.
y'(-1)>0;
y(0.5)<0;
y'(1.5)<0;
y'(3)>0.
Це не так важко перевіряти, оскільки знаменник в похідній завжди додатний, а в чисельнику всьго два простих множники.
Нас же цікавить не значення похідної, а лише її знак.
Результати визначення інтервалів знакосталості похідної потрібні, щоб з'ясувати чи максимуму, а чи мінімуму функція досягає в критичній точці.
ymax=y(0)=0 - локальний максимум функції.
ymin=y(2)=2 - локальний мінімум функції.
Систематизуємо дані у вигляді таблиці
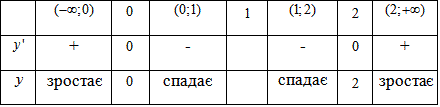
В кого багата практика, той за таблицею і екстремумами вже може уявити, що за функція задана та як її побудувати.
Е) Асимптоти функції.
Вертикальну асимптоту маємо з умови, що границя в точці рівна нескінченності:
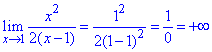
Таким чином x=1 - вертикальна асимптота.
Похилу асимптоту y=k*x+b отримаємо після обчислення границь при змінній прямуючій до безмежності:
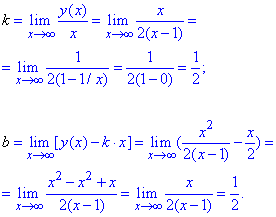
Кінцеве рівняння похилої асимптоти y=(x+1)/2.
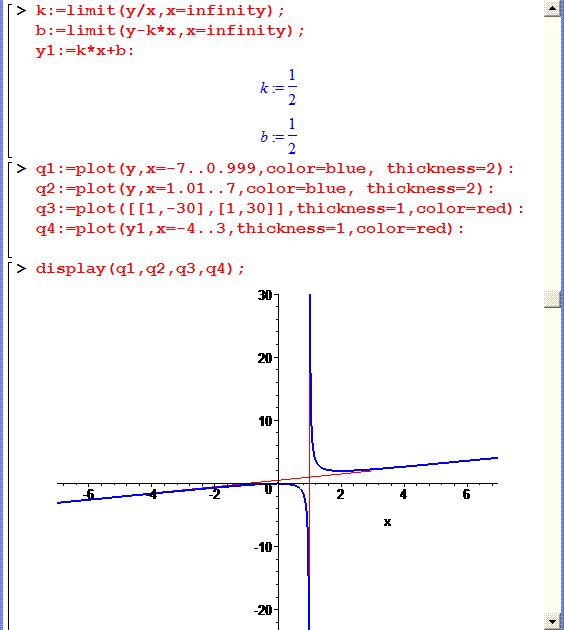
Виконаємо побудову графіка функції та обчислення границь в мейплі.
Для цього нам потрібен наступний код
restart:with(plots):
y:=x2/2/(x-1);
> k:=limit(y/x,x=infinity);
> b:=limit(y-k*x,x=infinity);
> y1:=k*x+b:
k := 1/2
b := 1/2
> q1:=plot(y,x=-7..0.999,color=blue, thickness=2):
> q2:=plot(y,x=1.01..7,color=blue, thickness=2):
> q3:=plot([[1,-30],[1,30]],thickness=1,color=red):
> q4:=plot(y1,x=-4..3,thickness=1,color=red):
> display(q1,q2,q3,q4);
Результати побудови наведені на рисунку
ЗАВДАННЯ 3 Дослідити і побудувати графік функції
y=x4/(x3-1)
Розв'язання: Область допустимих значень знаходимо з умови, що знаменник функції не приймає нульових значень
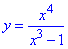
А) ОДЗ:
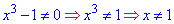, отже знову маємо два інтервали
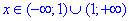
Б) Нулі функції:
при x=0, y(0)=0;
при y=0, x(0)=0.
В) Дослідження на парність:
Підстановка від'ємних значень
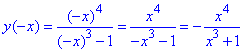
показує, що функція є ні парною, ні непарною.
Г) Знайдемо критичні точи функції:
За правилом частки обчислюємо похідну дробової функції
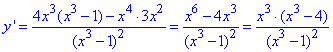
та з умови рівності похідної нулю
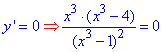
знаходимо дві x1=0,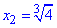 
- критичні точки.
Д) Інтервали зростання та спадання функції:
ymax=y(0)=0 - найбільше значення функції;
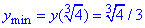- найменше значення функції.
Результати досліджень записуємо у таблицю
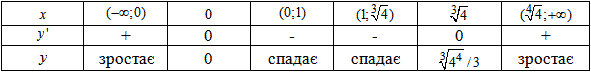
Е) Асимптоти функції.
Обчислюємо границю функції, коли змінна прямує до одиниці зліва та справа
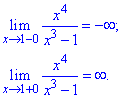
Границі прямують до плюс - мінус безмежності, отже маємо точку розриву ІІ роду.
Похилу асимптоту знаходимо через відповідні границі k, b
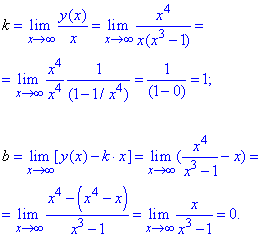
Таким чином пряма y=x є похилою асимптотою функції.
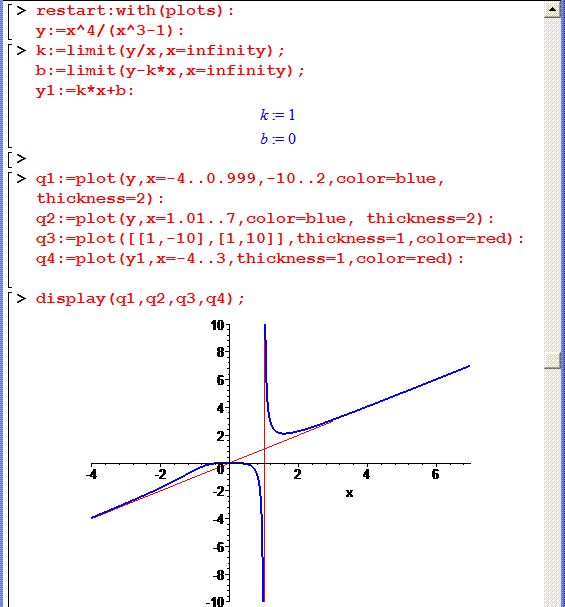
Виконаємо обчислення границь в Мейпл та побудову функції разом з асимптотами
> restart:with(plots):
> y:=x^4/(x^3-1):
> k:=limit(y/x,x=infinity);
> b:=limit(y-k*x,x=infinity);
> y1:=k*x+b:
k := 1
b := 0
> q1:=plot(y,x=-4..0.999,-10..2,color=blue, thickness=2):
> q2:=plot(y,x=1.01..7,color=blue, thickness=2):
> q3:=plot([[1,-10],[1,10]],thickness=1,color=red):
> q4:=plot(y1,x=-4..3,thickness=1,color=red):
> display(q1,q2,q3,q4);
Фрагмент програми наведено на рисунку
ЗАВДАННЯ 4 Знайти проміжки монотонності й екстремуми функції:
f(x)=1/8*(6x2-x3-16)
Розв'язання: ОДЗ: Поліном визначений на всій множині дійсних чисел xєR, тобто функція існує всюди
Знайдемо похідну заданої функції:
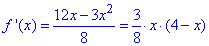
Знайдемо критичні точки з умови f'(x)=0
3.8*x*(4-x)=0, звідси x1=0 і x2=4 - критичні точки.
Перевіривши знак похідної між знайденими точками f'(1)>0, та скориставшись правилом чергування знаку похідної, запишемо проміжки монотонності й екстремум функції: на двох інтервалах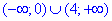 
– функція спадає;
та на одному (0;4) – маємо зростаючу функцію;
(0;-2) (мінімум) і (4;2) (максимум) – точки екстремуму функції.
В підсумку у Вас повинні вийти наступні результати
Графік функції наведено нижче
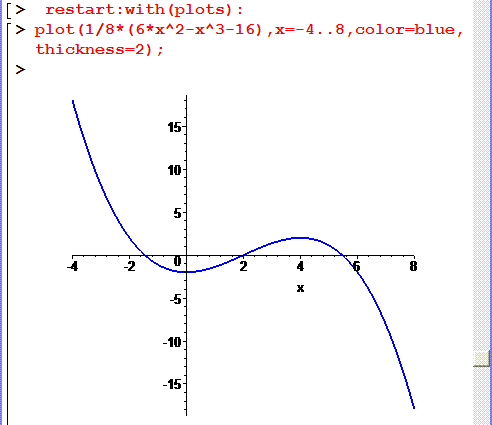
ЗАВДАННЯ 5 Виконати повне дослідження функції та побудувати її графік
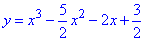Розв'язання: Проведемо аналіз трьохчлена за загальною схемою
А) Область визначення функції - множина дійсних чисел
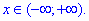
Б) Нулі функції:
при x=0,y=3/2;
при y=0 маємо три точки перетину осі x1=3, x2=1/2 і x3=-1.
В підсумку маємо чотири точки перетину координатних осей:
(0;3/2), (3;0), (1/2;0), (-1;0) .
В) Дослідження на парність:
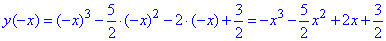
Бачимо, що функція не є парна, ні непарна.
Г) Знайдемо критичні точки функції:
Похідна заданої функції:
y'=3x2-5x-2 .
Далі особливі точки з умови y'=0,
3x2-5x-2=0 звідси x1=-1/3 і x2=2 - критичні точки.
Досліджуємо поведінку похідної між знайденими точками
y'(0)=-2<0, на сусідніх інтервалах похідна чергується (додатна), відповідно функція зростаюча.
Результати досліджень записуємо в таблицю
Д) Інтервали зростання та спадання, max і min точки функції:
ymax=y(-1/3)=50/27 - локальний максимум функції.
ymin=y(2)=-4,5 - локальний мінімум функції.
В допоміжну таблицю вносимо результати аналізу
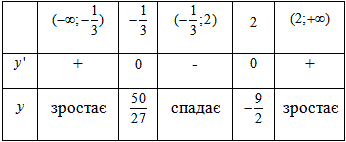
Е) Інтервали опулості та вгнутості функції:
Обчислюємо другу похідну
y''=6x-5;
та з умови рівності нулю знаходимо точку перегину
y''=0; 6x-5=0; x=5/6.
Далі досліджуємо знак другої похідної
y''(0)=-5; y''(1)=1.
Отже на інтервалі від мінус безмежності до точки перегину (-infinity;5/6) – функція опукла.
(5/6;infinity) –інтервал вігнутості ф-ї.
Є) Асимптот графік заданої функції не має, оскільки поліноміальна функція неперервна на всій області визначення.
Як будувати графік функції в Мейпл наведено на рисунку
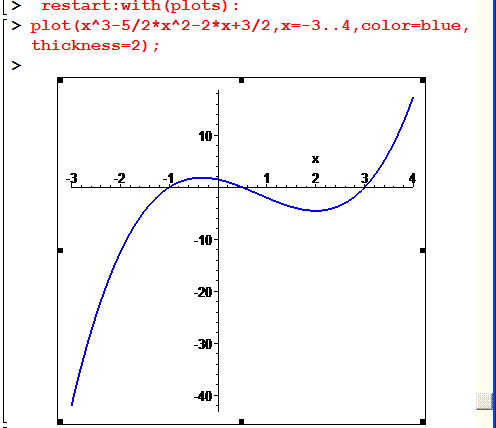
Код не складний і навчитися його використовувати в навчаьних цілях під силу кожному студенту, поєднувати теорію з практикою не так і складно.
Варто лише спробувати і Ви освоїте як мат. аналіз, так і математичні програми!
