Продовжуємо цикл публікацій із ЗНО підготовки на властивості елементарних функцій. Сьогодні розберемо приклади на парність та непарність функцій, формули перевірки парності та непарності, далі вивчатимемо періодичність тригонометричних функцій. Завдання досить прості, тому Ви швидко зможете засвоїти основні властивості функцій та алгоритми обчислень подібних завдань.
Розділ 22. Елементарні функції та їх властивості
Парність та непарність функцій
Приклад 22.12 Указати парну функцію.
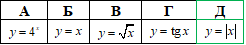
Розв'язування: Функція y=f(x) називається парною, якщо y(-x)=y(x).
Перевіримо парність y(x)=4x, для від'ємних значень маємо 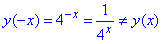 , робимо висновок що функція y(x)=4x не є парною;
, робимо висновок що функція y(x)=4x не є парною;
y(x)=x, тоді y(-x)=-x ≠y(x) - не є парною;
y(x)= √x, тоді 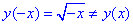 - не є парною;
- не є парною;
y(x)=tg(x), тоді y(-x)=tg(-x)=-tg(x)≠y(x) - не є парною;
y(x)=|x|, тоді y(-x)=|-x|=x=y(x) - функція є парною.
Відповідь: y=|x| – Д.
Приклад 22.13 Яка з наведених функцій є непарною?
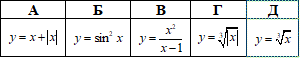
Розв'язування: Функція y=f(x) називається непарною, якщо y(-x)=-y(x).
Розглянемо y(x)=x+|x|, розпишемо y(-x)=-x+|-x|=-x+|x|≠y(x) - не є непарною;
y(x)=sin2(x), тоді y(-x)=sin2(-x)= sin2(x) |≠y(x) - не є непарною;
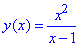 , тоді
, тоді 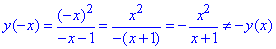 - не є непарною;
- не є непарною;
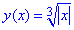 , розпишемо
, розпишемо 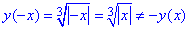 - не є непарною;
- не є непарною;
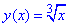 , тоді
, тоді 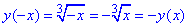 - функція є непарною.
- функція є непарною.
Відповідь: 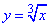 – Д.
– Д.
Приклад 22.14 Функція f(x) - парна, а функція g(x) - непарна. f(7)=-11, g(5)=-2. Обчислити 2f(-7)-3g(-5).
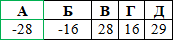
Розв'язування: Оскільки функція f(x) - парна, то f(-x)=f(x), звідси f(-7)=f(7)=-11.
Оскільки функція g(x) - непарна, то g(-x)=-g(x), звідси g(-5)=-g(5)=2.
Обчислюємо значення виразу
2f(-7)-3g(-5)=2•(-11)-3•2=-22-6=-28.
Відповідь: -28 – А.
Приклад 22.15 На рисунку зображено графік функції y=f(x), визначеної на проміжку [-4;4].
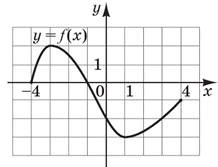
Знайти множину всіх значень x, для яких f(x) ≤-2.
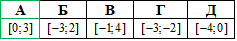
Розв'язування: Проведемо пряму y=-2 (паралельно осі Ox), та знайдемо такі значення x, при яких графік функції y=f(x) знаходиться під прямою y=-2
(і на прямій також, бо нерівність нестрога), тобто знайдемо розв'язки нерівності f(x) ≤-2:
x∈[0;3] .
Відповідь: [0;3] – А.
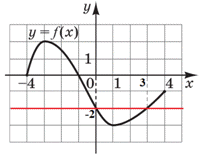
Приклад 22.16 За ескізом графіка y=ax+b вказати знаки параметрів a і b.
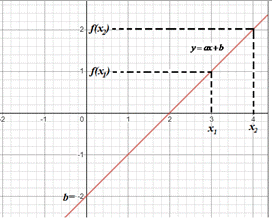
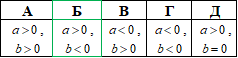
Розв'язування: Графіком функції y=ax+b є пряма. Функція зростає: f(x1)>f(x2), якщо x1>x2, або f(x1)<f(x2), якщо x1<x2, тоді a>0 (або якщо пряма утворює гострий кут з додатним напрямком осі Ox).
У завданні функція зростає, тому a>0.
Параметр b вказує на ординату перетину прямої y=ax+b з віссю Oy. На ескізі графіка b=-2<0.
Відповідь: a>0, b<0.
Приклад 22.39 Установити відповідність між функціями (1–4) та їх парністю (А–Д).
1. y=0 | А. На парність не досліджується |
Розв'язування: Функція y=y(x) парна, якщо y(-x)=y(x) (графік симетричний відносно осі Oy).
Функція y=y(x) непарна, якщо y(-x)=-y(x) (графік симетричний відносно початку координат).
Наведемо допоміжний рисунок, щоб Ви переконалися в правильності міркувань.
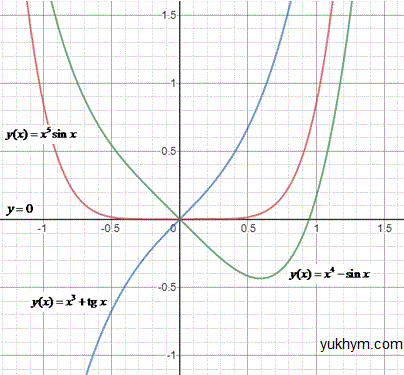
1. y=0 - функція і парна, і непарна (особливий випадок) 1 - Д.
Запам'ятайте цей момент, оскільки на цьому рідко наголошують.
На графіку задана функція зображена чорним кольором (вісь Ox).
2. y(x)=x3+tg(x).
y(-x)=(-x)3+tg(-x)=-3-tg(x)=-(x3+tg(x))=-tg(x) - функція непарна 2 - В.
Функція y(x)=x3+tg(x) зображена синім кольором (симетрична відносно початку координат).
3. y(x)=x4-sin(x).
y(-x)=(-x)4-sin(-x)=x4+sin(x)≠±y(x) - функція ні парна, ні непарна 3 - Г.
Функція на графіку y(x)=x3+tg(x) зображена зеленим кольором.
4. y(x)=x5·sin(x).
y(-x)=(-x)5•sin(-x)=-x5•(-sin(x))=x5•sin(x)=y(x) - функція парна 4 - Б.
На графіку y(x)=x5·sin(x) зображена червоним кольором (симетрична відносно осі Oy).
Приклад 22.52 За якого найбільшого значення параметра a функція 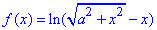 буде непарною?
буде непарною?
Розв'язування: Функція f(x) непарна, якщо f(-x)=-f(x).
Складаємо рівняння з умови на парність
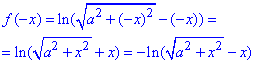 .
.
Розв'яжемо логарифмічне рівняння:
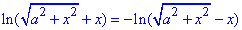 відносно параметра a.
відносно параметра a.
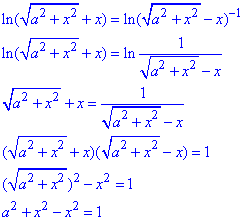
a2=1,
a1=1,
a2=-1.
a=1 - найбільше значення, за якого функція буде непарною.
Відповідь: 1.
Знання властивостей функцій потрібні для швидкого їх дослідження, що перевіряється в шкільній практиці та продовжують вивчати у ВУЗах. Вступні тести є перехідним етапом, але через обмеженість часу Ви маєте вивчити великий об'єм матеріалу, тому починайти готуватися завчасно.
- Вас може зацікавити:
- Область визначення складних кореневих, логарифмічних, тригонометричних функцій
- Дослідження функції на монотонність, екстремуми, побудова графіка
- Дослідження функції на монотонність, екстремуми, побудова графіка
- Паралельне перенесення графіку функції, симетричне відображення, розтяг та стиск


