Переходимо до останніх завдань із ЗНО підготовки на геометричні перетворення функції. Теорія та прості приклади на застосування зсуву та паралельного перенесення графіку функцій, його розтягу та стиску розглянуто раніше. Далі на готових відповідях Ви навчитеся за виглядом функцій знаходити їх графіки, області визначення та області значень, самостійно виконувати найпростіші геометричні перетворення. Завдань багато і на щоб розібратися з усіма Вам необхідно уважно переглянути та усвідомити, що від Вас вимагають в умові.
Побудова графіків функцій за допомогою паралельного перенесення, симетричного відображення, розтягу та стиску
Приклад 23.21 Установити відповідність між функціями (1–4) та їх графіками (А–Д).
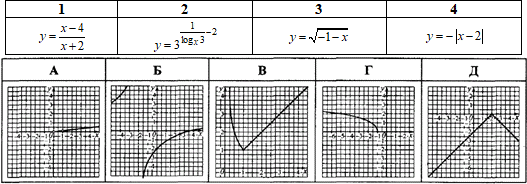
Розв'язування: 1. Перетворимо вихідну формулу функції
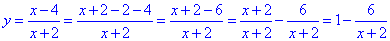
Бачимо, що графік функції y=(x-4)/(x+2) отримують в результаті наступних геометричних перетворень графіка функції y=-1/x (гіпербола з гілками у ІІ у ІV чвертях):
а) паралельним перенесенням на 2 одиниці ліворуч;
б) на 1 одиницю вгору і розтягом у 6 разів, отже 1 - Б.
В результаті отримаємо графік y=(x-4)/(x+2).
Виконуємо побудову елементарної оберненої функції та заданої в умові
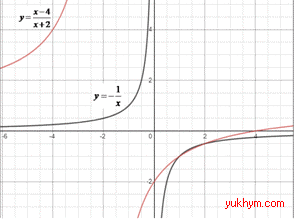
2. Враховуючи властивості логарифма, задану функцію перетворимо до вигляду
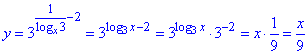
І не забувайте врахувати ОДЗ логарифма при побудові рисунку, тому графіком функції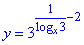 
є пряма y=x/9 з областю визначення:
x>0 і x≠-1 (за властивістю логарифма logx3). 2 - А.
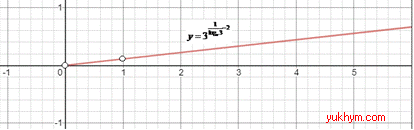
3. Графік кореневої функції y=√(-x-1) отримують в результаті перетворень графіка функції y=√x:
а) симетричним відображенням відносно осі Oy (y=√(-x));
б) паралельним перенесенням на 1 одиниці ліворуч (y=√(-1-x)), отже 3 - Г.
На рисунку нижче наведені обидва графіки.
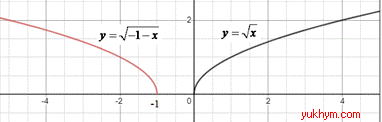
4. Графік модуль функції y=-|x-2| отримують в результаті перетворень графіка функції y=x:
а) симетричним відображенням відносно осі Oy (y=|x|);
б) паралельним перенесенням на 2 одиниці праворуч (y=|x-2|);
в) симетричним відображенням відносно осі Ox усіх додатних y ( y=-|x-2|), отже 4 - Д.
Побудова графіків функцій допомагає краще запам'ятати як змінюються формули функцій при перенесенні та симетричному відображенні. Таких завдань попереду багато і більшість по можливості ми будемо доповнювати ескізами графіків функцій.
Приклад 23.22 Установити відповідність між функціями (1–4) та їх графіками (А–Д).
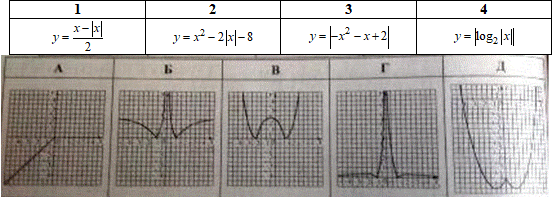
Розв'язування: 1. Графік функції y=(x-|x|)/2 отримують шляхом розкриття модуля:
при x≥0 маємо: y=(x-|x|)/2=0,
при x<0 маємо: y=(x+x)/2=x. 1 - А.
2. Графік функції y=x^2-2|x|-8 отримують методом розкриття модуля:
при x>0 маємо: y=x^2-2x-8 права частина параболи,
при x<0 маємо: y=x^2+2x-8 ліва частина параболи. 2 – Д.
3. Графік функції y=|-x^2-x+2| отримують з графіка y=-x^2-x+2:
y=-x^2-x+2 - парабола з гілками вниз (a=-1<0), з абсцисою у вершині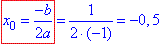 
та точкою перетину з віссю ординат (0;2).
Частину графіка, яка знаходиться під віссю Ox (від'ємні значення y) симетрично відображають відносно осі абсцис (Ox) і отримуємо графік функції y=|-x^2-x+2|. 3 – В.
4. Графік функції y=|log2|x|| отримують з графіка y=log2x:
Спочатку частину графіка, яка знаходиться під віссю Ox симетрично відображаємо відносно осі абсцис і отримуємо графік функції y=|log2x| (причому частину графіка під віссю абсцис не залишаємо).
Далі отриманий графік симетрично відображають відносно осі ординат і отримуємо графік функції y=|log2|x||. 4 – Б.
Для підготовки до ЗНО тестувань спробуйте самостійно розв'язати не менше двох подібних завдань.
Приклад 23.23 Установити відповідність між функціями (1–4) та їх графіками (А–Д).
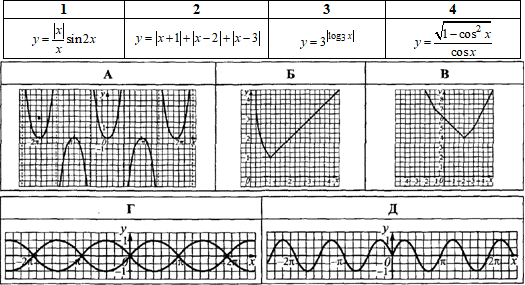
Розв'язування: 1. Графік функції y=|x|in(2x)/x
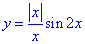отримують шляхом розкриття модуля:
при x>0 маємо:
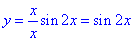
при x<0 маємо:
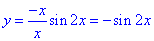1 – Д.
2. Графік функції y=|x+1|+|x-2|+|x-3| отримують методом розкриття модулів:
при x<-1 маємо:
y=-x-1-x+2-x+3=-3x+4 – частина прямої;
при -1<x<2 маємо:
y=x+1-x+2-x+3=-x+6 – частина прямої;
при 2<x<3 маємо:
y=x+1=x-2-x+3=x+2 – частина прямої;
при x>3 маємо:
y=x+1+x-2+x-3=3x-4 – частина прямої.
В результаті отримаємо ламану, що зображена на рисунку – В.
3. Графік функції y=3^|log3(x)| отримують методом розкриття модуля і показниково-логарифмічної функції:
при x>1 маємо: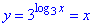 
– частина прямої;
при 0<x<1 маємо: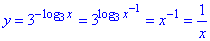 
y=1/x частина гіперболи.
З тестових відповідей підходить варіант – Б.
4. Графік функції 
отримують за властивістю тригонометричних функцій та розкриття модуля:
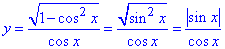
при x∈(0+2πk;π+2πk), k∈Z, маємо:
y=sin(x)/cos(x)=tg(x) - частина лінії тангенса;
при x∈(π+2πk;2π+2πk), k∈Z маємо:
y=-sin(x)/cos(x)=-tg(x) - частина лінії тангенса. 4 – А.
На ЗНО тестах модулі та тригонометричні функції зустрічаються досить часто, тому добре вивчіть їх властивості.
Приклад 23.24 Установити відповідність між рівняннями (1–4) та їх графіками (А–Д).
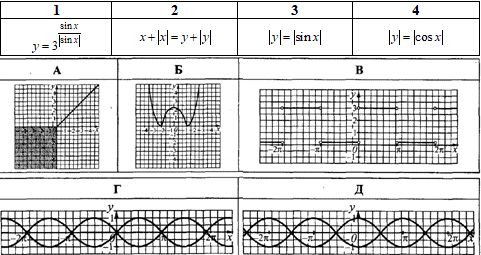
Розв'язування: 1. Графік функції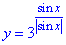 
отримують розкриттям модуля та властивостей тригонометричних функцій:
при x∈(0+2πk;π+2πk), k∈Z маємо:
y=3^(sin(x)/sin(x))=3 - частина прямої;
при x∈(π+2πk;2π+2πk), k∈Z маємо:
y=3^(-sin(x)/sin(x))=3^(-1)=1/3 - частина прямої. 1 – В.
2. Щоб побудувати графік функції x+|x|=y+|y| розкриваємо модулі для змінних з кожної чверті:
при x>0, y>0 маємо:
x+x=y+y, 2x=2y, x=y - частина прямої;
при x>0, y<0 маємо:
x+x=y-y, 2x=0, x=0 - частина осі Oy;
при x<0, y>0 маємо:
x-x=y+y, 0=2y, y=0 - частина осі Ox;
при x<0, y<0 маємо:
x-x=y-y, 0=0 - частина координатної площини. 2 - А.
Уважно перегляньте як розкривали модулі та повторіть правила.
3. Графік функції |y|=sin(x) отримують розкриваючи модулі для синуса:
при x∈(0+2πk;π+2πk), k∈Z, y>0 маємо:
y=sin(x) - частина синусоїди;
при x∈(0+2πk;π+2πk), k∈Z, y<0, маємо:
-y=sin(x), y=-sin(x) - частина синусоїди;
при x∈(π+2πk;2π+2πk), k∈Z, y>0 маємо:
y=sin(x) - частина синусоїди;
при x∈(π+2πk;2π+2πk), k∈Z, y<0 маємо:
-y=sin(x), y=-sin(x) - частина синусоїди. 3 - Г.
4. Графік функції |y|=|cos(x)| отримують методом розкриття модуля:
при x∈(-Pi/2+2πk;-Pi/2+2πk), k∈Z, y>0 маємо:
y=cos(x) - частина косинусоїди;
при x∈(-Pi/2+2πk;-Pi/2+2πk), k∈Z, y<0 маємо:
-y=cos(x), y=-cos(x) - частина косинусоїди;
при x∈(Pi/2+2πk;3Pi/2+2πk), k∈Z, y>0 маємо:
y=-cos(x) - частина косинусоїди;
при x∈(Pi/2+2πk;3Pi/2+2πk), k∈Z, y<0 маємо:
-y=-cos(x), y=cos(x) - частина косинусоїди. 4 - Д.
Приклад 23.25 Задано функцію y=f(x) з множиною значень [-2;5]. Установити відповідність між функціями (1–4) та їхніми множинами значень (А–Д).
Розв'язування: 1. Графік функції y=f(x)+2 отримали паралельним перенесенням на 2 одиниці вгору графіка функції y=f(x).
Оскільки -2≤f(x)≤5, то -2+2≤f(x)+2≤5+2, тобто 0≤f(x)+2≤7.
E(y)=[0;7] - множина значень функції y=f(x)+2. 1 - Г.
2. Графік функції y=-f(x) отримали симетричним відображенням y=f(x) відносно осі Ox (абсцис).
Оскільки -2≤f(x)≤5, то 2≥f(x) ≥-5, тобто -5≤f(x)≤2.
E(y)=[-5;2] - множина значень функції y=-f(x). 2 - Д.
3. Графік функції y=2f(x) отримали розтягом y=f(x) удвічі відносно осі Ox (абсцис).
Оскільки -2≤f(x)≤5, то -2•2≤2•f(x)≤2•5, тобто -4≤2•f(x)≤10.
E(y)=[-4;10] - множина значень функції y=2f(x). 3 - Б.
4. Графік функції y=|f(x)| отримали симетричним відображенням y=f(x) відносно осі Ox (абсцис) лише ту частину, яка знаходилася під віссю Ox.
Оскільки -2≤f(x)≤5, то -2≤|f(x)|≤5.
E(y)=[0;5] - множина значень функції y=|f(x)|. 4 - А.
Приклад 23.26 Задано функцію y=φ(x) з областю визначення [-4;10]. Установити відповідність між функціями (1–4) та їхніми областями визначення (А–Д).
Розв'язування: 1. Графік функції y=φ(x+4) отримали паралельним перенесенням на 4 одиниці ліворуч (у від’ємному напрямку осі Ox) графіка функції y=φ(x).
Оскільки -4≤x≤10, то -4-4≤x-4≤10-4, тобто -8≤x-4≤6.
D(y)=[-8;6] - область визначення функції y=φ(x+4). 1 - Д.
2. Графік функції y=φ(x-4) отримали паралельним перенесенням на 4 одиниці праворуч (у додатному напрямку осі Ox) графіка функції y=φ(x).
Оскільки -4≤x≤10, то -4+4≤x+4≤10+4, тобто -0≤x+4≤14.
D(y)=[0;14] - область визначення функції y=φ(x+4). 2 - Б.
3. Графік функції y=φ(x)+5 отримали паралельним перенесенням на 5 одиниць вгору (у додатному напрямку осі Oy) графіка функції y=φ(x). Область визначення функцій y=φ(x) і y=φ(x)+5 однакова.
D(y)=[-4;10] - область визначення функції y=φ(x)+5. 3 - А.
4. Графік функції y=φ(x-5)-3 отримали паралельним перенесенням на 5 одиниці праворуч (у додатному напрямку осі Ox) та на 3 одиниці вниз (у від’ємному напрямку осі Oy) графіка функції y=φ(x).
Оскільки -4≤x≤10, то -4+5≤x+5≤10+5, тобто 1≤x+5≤15.
D(y)=[1;15] - область визначення функції y=φ(x-5)-3. 4 - Г.
Приклад 23.27 Задано функцію y=h(x) з областю визначення [-2;6]. Установити відповідність між функціями (1–4) та їхніми областями визначення (А–Д).
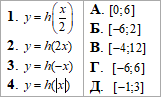
Розв'язування: 1. Графік функції y=h(x/2) розтягом удвічі відносно осі Oy графіка функції y=h(x).
Оскільки -2≤x≤6, то -2•2≤2•x≤2•6, тобто -4≤2•x≤12.
D(y)=[-4;12] – область визначення функції y=h(x/2). 1 - В.
2. Графік функції y=h(2x) стисненням удвічі відносно осі Oy графіка функції y=h(x).
Оскільки -2≤x≤6, то -2/2≤x/2≤6/2, тобто -1≤x/2≤3.
D(y)=[-1;3] – область визначення функції y=h(2x). 2 - Д.
3. Графік функції y=h(-x) отримали симетричним відображенням відносно осі Oy (ординат) графіка функції y=h(x).
Оскільки -2≤x≤6, то 2≤x≤-6, тобто -6≤x≤2.
D(y)=[-6;2] – область визначення функції y=h(-x). 3 - Б.
4. Графік функції y=h(|x|) отримали симетричним відображенням правої частини графіка функції y=h(x) відносно осі Oy (ординат).
Оскільки -2≤x≤6, то -6≤x≤6. Це не зовсім тривіально для Вас, але спробуйте собі уявити, що початкова функція визначена на x∈[-2;6]. Модуль з |x| при x=-6 якраз рівний правому краю проміжку x∈[-2;6].
D(y)=[-6;6] – область визначення функції y=h(|x|). 4 - Г.
Приклад 23.28 На рисунку зображено графік функції y=f(x), спадної на проміжку (-∞;+∞).
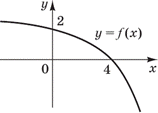
Установіть відповідність між функцією (1–4) та точкою перетину її графіка з віссю Ox (А–Д).
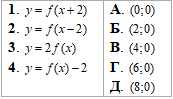
Розв'язування: Графік функції y=f(x) перетинає вісь Ox в точці (4;0).
1. Графік функції y=f(x+2) отримали паралельним перенесенням на 2 одиниці ліворуч (у від’ємному напрямку осі Ox) графіка функції y=f(x).
Тому графік функції y=f(x+2) перетинає вісь Ox в точці (2;0)
(зменшили абсцису точки перетину на 2 одиниці). 1 – Б.
2. Графік функції y=f(x-2) отримали паралельним перенесенням на 2 одиниці праворуч (у додатному напрямку осі Ox) графіка функції y=f(x).
Тому графік функції y=f(x-2) перетинає вісь Ox в точці (6;0)
(збільшили абсцису точки перетину на 2 одиниці). 2 - Г.
3. Графік функції y=2f(x) отримали розтягом y=f(x) удвічі відносно осі Ox (абсцис).
Тому графік функції y=2f(x) перетинає вісь Ox в точці (4;0)
(абсцису точки перетину не змінили). 3 - В.
4. Графік функції y=f(x)-2 отримали паралельним перенесенням на 2 одиниці вниз графіка функції y=f(x).
Тому графік функції y=f(x)-2 перетинає вісь Ox в точці (0;0)
(абсциса і ордината точки перетину співпали у початку координат). 4 - А.
Ви можете використовувати завдання в шкільній програмі, готувати на їх основі презентації, а головне мати уявлення як це легко реалізувати з допомогою простих геометричних перетворень.
