Відшукання локальних максимумів і мінімумів не обходиться без диференціювання і потрібне при дослідженні функції та побудові її графіка.
Точка x0 називається точкою локального максимуму (або мінімуму) функції y=f(x), якщо існує такий окіл 0<|x-x0|<delta цієї точки, який належить області визначення функції, і для всіх аргументів x<x0 з цього околу виконується нерівність f(x)<f(x0) (або f(x)>f(x0)).
Точки максимуму і мінімуму називаються точками екстремуму функції , а значення функції в екстремальних точках – її екстремальними значеннями.
НЕОБХІДНА ОЗНАКА ЛОКАЛЬНОГО ЕКСТРЕМУМУ:
Якщо функція має в точці x0 локальний екстремум, то її похідна або рівна нулю f'(x0)=0 , або не існує. Точки, які задовольняють виписаним вище вимогам ще називають критичними точками. Проте не в кожній критичній точці функція має екстремум. Відповідь на питання: чи буде критична точка точкою екстремуму дає наступна теорема.
ДОСТАТНЯ ОЗНАКИ ІСНУВАННЯ ЕКСТРЕМУМУ ФУНКЦІЇ
Теорема І. Нехай функція y=f(x) неперервна в деякому інтервалі, що містить критичну точку x0, і диференційована у всіх точках цього інтервалу (за винятком, можливо, самої точки x0). Тоді для точки x0 функція має максимум, якщо для аргументів x<x0 виконується f'(x0)>0, а для x>x0 умова f'(x0)<0.
Якщо ж для x<x0 похідна менша нуля f'(x0)<0 , а для x>x0 більша нуля f'(x0)>0, то для точки x=x0 функція має мінімум.
Теорема ІІ. Нехай функція два рази диференційована в околі точки x0 і похідна рівна нулю f'(x0)=0 . Тоді в точці x=x0 функція має локальний максимум, якщо друга похідна менша нуля f"(x0)<0 , і локальний мінімум, якщо друга похідна додатна f"(x0)>0.
Якщо ж f"(x0)=0, то точка x=x0 може й не бути точкою екстремуму.
При дослідженні функцій на екстремуми використовують обидві теореми. Перша на практиці простіша, оскільки не вимагає знаходження другої похідної.
ПРАВИЛА ЗНАХОДЖЕННЯ ЕКСТРЕМУМІВ (МАКСИМУМІВ І МІНІМУМІВ) ЗА ДОПОМОГОЮ ПЕРШОЇ ПОХІДНОЇ
1) знайти область визначення D(f);
2) знайти похідну f'(x);
3) знайти критичні точки x0;
4) дослідити знак похідної f'(x) на інтервалах, які отримали від розбиття критичними точками області визначення.
При цьому критична точка x0 є точкою мінімуму, якщо при переході через неї зліва направо f'(x) змінює знак з від'ємного "-" на додатній "+", в протилежному випаду x0 є точкою максимуму.
Замість даного правила можна визначати другу похідну f"(x) і досліджувати згідно другої теореми.
5) обчислити значення функції в точках екстремуму.
Розглянемо тепер дослідження функції на екстремуми на конкретних прикладах.
Приклади. Збірник В.Ю. Клепко, В.Л. Голець "Вища математика в прикладах і задачах"
1. (4.53.7) y=x2e-x
Ров'язування: 1) Областю визначення буде множина дійсних чисел D(y): x∈R
2) Знаходимо похідну функції
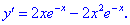
3) Прирівнявши її до нуя, визначаємо критичні точки
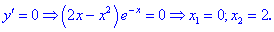
Вони розбивають область визначення на такі інтервали
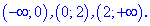
4) Дослідимо знак похідної на знайдених інтервалах методом підстановки внутрішніх точок
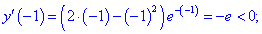
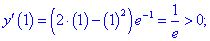
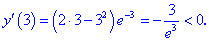
Таким чином перша точка x=0 є точкою мінімуму, а друга x=2 - точкою максимуму.
5) Обчислюємо значення ординати точкок
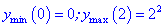
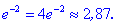
На цьому і грунтуються дослідження функцій на екстремуми.
Далі навчимо Вас будувати графіки, асимптоти і виконувати дослідження функції в математичному пакеті Мейпл.
Для побудови першої функції на інтервалі, де добре видно локальний максимум скористаємося наступним кодом:
restart; with(plots);
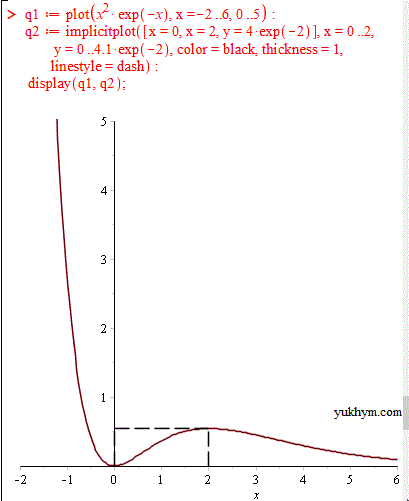
q1 := plot(x^2*exp(-x), x = -2 .. 6, 0 .. 5);
q2 := implicitplot([x = 0, x = 2, y = 4*exp(-2)], x = 0 .. 2, y = 0 .. 4.1*exp(-2), color = black, thickness = 1, linestyle = dash);
display(q1, q2);
В результаті отримаємо графік на якому в точці x=0 маємо локальний мінімум, а в точці x=2 – локальний максимум.
2. (4.53.9) y=ln√(1+x^2)+arctan(x)
Ров'язування: 1) Областю визначення буде множина дійсних чисел D(y): x∈(-∞;+∞), оскільки корінь завжди більший одиниці
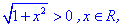
і функція арктангенс визначена на всій дійсній осі .
2) Знаходимо похідну логарифма та арктангенса
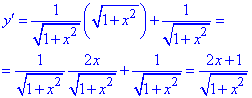
3) З умови рівності похідної нулю знаходимо критичну точку
2x+1=0, x=-1/2=-0,5.
Вона розбиває область визначення на два інтервали
x∈(-∞;-0,5)∪(0,5;+∞).
4) Визначимо знак похідної в кожній з областей
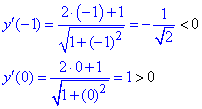
Отже в критичній точці x=-0,5 функція приймає мінімальне значення.
5) Обчислимо екстремум функції
y(-0.5)=ln(1+(-0,5)^2)+arctan(-0,5)≈-0,2405
Ще одне завдання детально проаналізована на локальний екстремум.
Для наочності, покажемо як виглядає локальний мінімум на графіку.
Для цього в Мейплі наберемо наступний код та обчислимо
q1 := plot(ln(x^2+1)+arctan(x), x = -8 .. 5);
q2 := implicitplot([x = 0, 5], x = -5 .. 5, y = -1 .. 0, color = black, thickness = 1, linestyle = dash);
display(q1, q2);
Отримаємо наступний графік функції
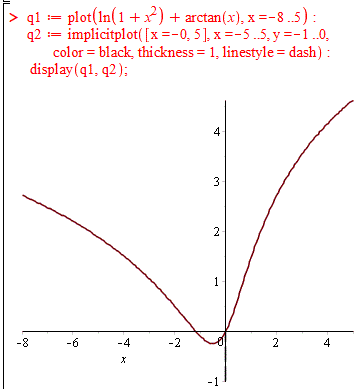
3. (4.53.13) 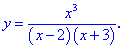
Ров'язування: 1) Функція визначена коли знаменник дробу не перетворюється в нуль
(x-2)(x+3)≠0⇒x=2, x=-3.
Отже область визначення складається з трьох інтервалів
D(y): x∈(-∞;-3)∪(-3;2)∪(2;+∞)
2) Обчислимо похідну
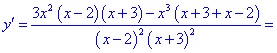
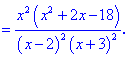
3) Прирівнюємо похідну до нуля і знаходимо критичні точки.
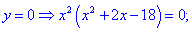
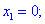
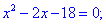
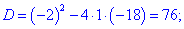
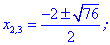
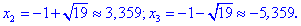
4) Встановлюємо знак похідної в кожній з областей підстановкою відповідних значень.
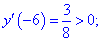
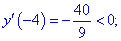
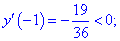
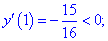
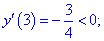
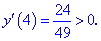
Таким чином перша точка x3=-5,359 є точкою локального максимуму, а x2=3,359 локального мінімуму. В x1=0 маємо перегин функції, але про нього буде більше матеріалу в наступних статтях.
5) Знаходимо значення в критичних точках
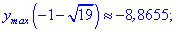
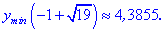
Незважаючи на те, що значення функції ymax<ymin, перша точка є точкою локального максимуму, а дуга – мінімуму. Не лякайтеся, якщо в Вас вийдуть подібні результати, при визначенні локальних екстремумів такі ситуації нормальне явище.
Побудуємо графік функції разом з вертикальними асимптотами в Мейплі:
q1 := plot(x^3/(-2+x)/(x+3), x = -8 .. 8, discont = true);
q2 := implicitplot([x=-3,x = 2], x = -5 .. 5, y = -30 .. 30, color = black, thickness = 1, linestyle = dash);
display(q1, q2);
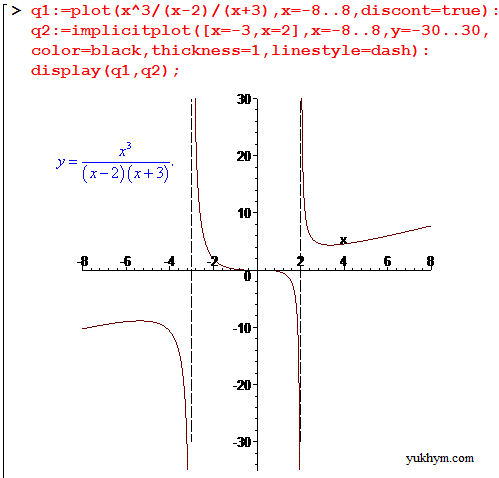
З графіку бачимо, що функція має похилу асимптоту, але як про те як скласти рівняння похилих асимптот поговоримо в наступнй статті.
Попереду Вас чекає багато готових розв'язків на повне дослдження функції, знаходження асимптот, інтервалів опуклості та вгнутості. Тож залишайтеся з нами та беріть максимум користі для навчання зі сторінок сайту!


