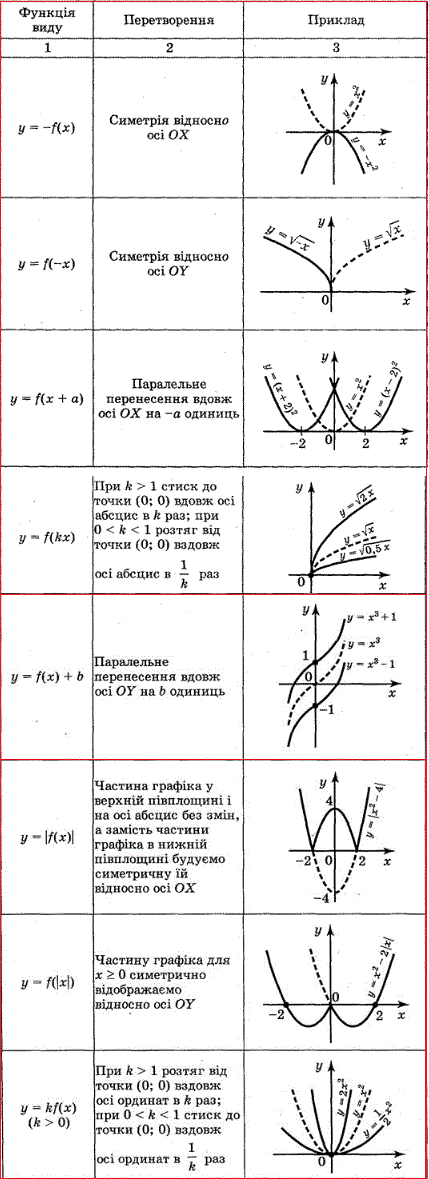
Основними методами геометричних перетворень графіків функцій є симетрія відносно осей Ox, Oy;
паралельне перенесення відносно осей Ox, Oy;
стиск та розтяг графіків відносно осей; відображення частини графіка під віссю Ox нагору (аналог модуль функції) і навпаки;
поворот площини навколо певної точки. В шкільному курсі Вас навчають як геометричні перетворення використовувати до графіків функцій та як це впливає на область визначення та область значень. Всі перелічені вище перетворення необхідні, щоб швидко навчити Вас будувати графіки функцій.
Основні геометричн перетворення графіка функцї
Для повторення шкільних матеріалів, які Ви повинні вільно вміти використовувати, уважно перегляньте таблицю в якій проілюстровані вісім основних перетворень графіка функції у = f(x):
у = -f(x); у = f(-x); у = f(x) + b; у = f(x + a); у = af(x); у = f(ax); у = f(|x|); у =|f(x)|.
Переходимо до практики застосування геометричних перетворень для графіків функцій та проаналізуємо готові відповіді до завдань із ЗНО підготовки. Завдання добре розписані, крім того основні методи перетворень виділені в ході розв'язування завдань. Всього розв'язано 33 приклади, частина з яких увійшли до наступних публікацій.
Побудова графіків функцій за допомогою геометричних перетворень
Приклад 23.1 Вказати формулу функції, графік якої отримують із графіка y=1/x у результаті його паралельного перенесення в додатному напрямі осі Oy на 5 одиниць.
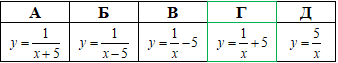
Розв'язування: Графік функції y=f(x)+a можна одержати із графіка функції y=f(x) за допомогою паралельного перенесення вздовж осі Oy на a одиниць угору (в додатному напрямі осі Oy), якщо a>0, і на a одиниць униз (у від’ємному напрямі осі Oy), якщо a<0.
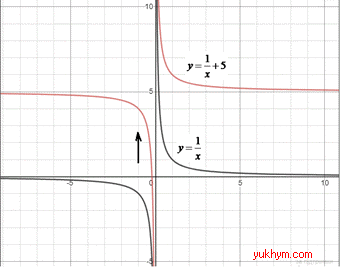
Отже, з графіка гіперболи y=1/x, у результаті його паралельного перенесення в додатному напрямі осі Oy на 5 одиниць, отримаємо графік функції y=1/x+5.
Це відповідає варіанту Г тестів.
Відповідь: y=1/x+5 – Г.
(В усіх завданнях графік чорним кольором є основним, а червоним кольором графік отриманий після геометричних перетворень)!
Приклад 23.2 На якому з наведених рисунків зображено ескіз графіка функції y=4-(x-1)^2?
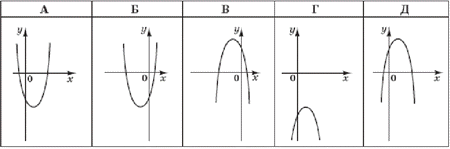
Розв'язування: Графік функції y=f(x+b) можна одержати із графіка функції y=f(x) за допомогою паралельного перенесення вздовж осі Ox на b одиниць праворуч (в додатному напрямі осі Ox), якщо b<0, і на b одиниць ліворуч (у від’ємному напрямі осі Ox), якщо b>0.
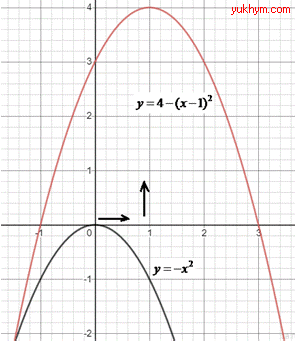
Отже, з графіка функції y=-x^2 (парабола) отримали y=4-(x-1)2 паралельними перенесеннями на 1 одиницю праворуч і на 4 одиниці вгору, тобто на вектор p(1;4).
Відповідь: Д.
Приклад 23.4 Областю значень функції y=f(x) є проміжок [-4;16]. Знайти область значень функції y=1/4•f(x).

Розв'язування: Завдання на область визначення та область значень досить поширені, тому запам'ятайте схему обчислень.
Оскільки функцію y=1/4•f(x) отримують з функції y=f(x) стисненням у 4 рази до осі Ox, то область значень (множина y) теж стиснеться у 4 рази.
Формулами це може мати запис
-4•1/4≤1/4•f(x)≤16•1/4, звідси
-1≤1/4•f(x)≤4.
Замість f(x) можете використовувати в нерівностях y, такі позначення будуть рівносильні для області значень.
Отже, E(y)=[-1;4] - область значень функції 1/4•f(x).
Відповідь: [-1;4] – В.
Приклад 23.5 На якому з рисунків зображено графік функції y=-2^x?
Розв'язування: Графік функції y=-f(x) можна одержати із графіка функції y=f(x) за допомогою симетричного відображення відносно осі Ox (абсцис).
Відповідний рисунок показникової функції до та після геометричного перетворення має вигляд.
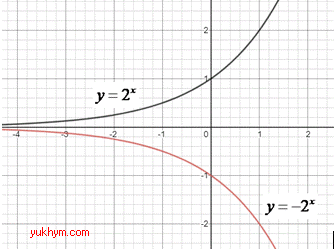
Відповідь: Г.
Приклад 23.6 Вказати формулу функції, графік якої отримують із графіка функції y=x^3 у результаті його паралельного перенесення в додатному напрямі осі Ox на 4 одиниці.
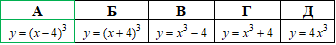
Розв'язування: З графіка функції y=x^3, у результаті його паралельного перенесення в додатному напрямі осі Ox на 4 одиниці, отримаємо функцію y=(x-4)^3.
Побудуємо зсув кубічної функції згідно умови.
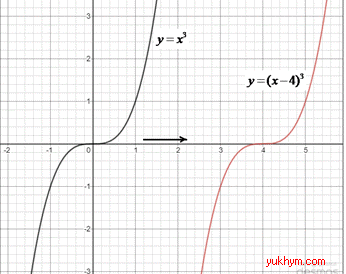
Відповідь: y=(x-4)^3 – А.
Приклад 23.7 На якому з рисунків зображено графік функції y=√(x+1)?
Розв'язування: З графіка функції y=√x, у результаті його паралельного перенесення у від’ємному напрямі осі Ox на 1 одиницю, отримаємо функцію y=√(x+1).
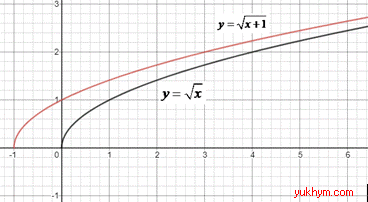
Відповідь: Д.
Приклад 23.8 Вказати формулу функції, графік якої отримують із графіка функції y=sin(x) у результаті його розтягування від осі Oy у 8 разів?
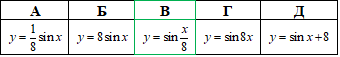
Розв'язування: Графік функції y=f(c•x) можна одержати із графіка функції y=f(x) за допомогою розтягу від осі Oy у c разів, якщо 0<c<1, і за допомогою стиснення до осі Oy у c разів, якщо c>1.
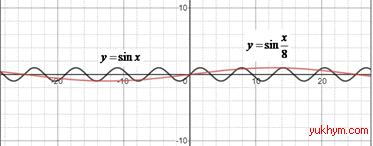
Отже, з графіка функції y=sin(x), у результаті його розтягу до осі Oy у 8 разів, отримаємо функцію y=sin(x/8).
Відповідь: y=sin(x/8)– В.
Приклад 23.9 Областю визначення функції y=f(x) є проміжок [-4;6].
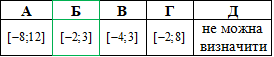
Знайти область визначення функції y=f(2x).
Розв'язування: Оскільки функцію y=f(2x) отримують з функції y=f(x) стисненням удвічі до осі Oy, то D(y)=[-2;3] - область визначення функції y=f(2x) (область визначення звузили у 2 рази).
Відповідь: [-2;3] – Б.
Приклад 23.10 На рисунку зображено ескіз графіка функції y=f(x). На якому з рисунків зображено ескіз графіка функції y=f(-x)?
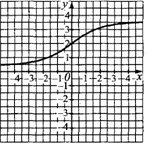
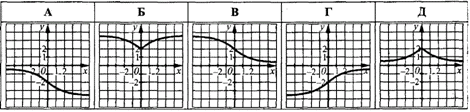
Розв'язування: Графік функції y=f(-x) можна одержати із графіка функції y=f(x) за допомогою симетричного відображення відносно осі Oy (ординат). Перегляньте уважно кожен з варіантів тестових відповідей та переконайтесь, що це В.
Відповідь: В.
Приклад 23.33 Найбільшим значенням функції y=f(x) є число 8. Знайти:
1) найбільше значення функції y=0,3f(4x+5)-1;
2) найменше значення функції y=-3f(2x-5).
Розв'язування: Область значень для функцій y=f(x), y=f(4x+5) і y=f(2x-5) однакова, оскільки змінення відбувається лише в межах осі Ox. Тому f(4x+5)≤8,
звідси
0,3•f(4x+5)≤0,3•8,
0,3•f(4x+5)≤2,4,
0,3•f(4x+5)-1≤2,4-1,
0,3•f(4x+5)-1≤ 1,4.
f(2x+5)≤8,
звідси
-3•f(2x+5) ≥-3•8,
-3•f(2x+5) ≥-24.
Отже, найбільшим значенням функції y=0,3f(4x+5)-1 є число 1,4;
найменшим значенням функції y=-3f(2x-5) є число -24.
Відповідь: 1,4; -24.
Попереду Вас чекають більше 20 готових прикладів на геометричні перетворення графіків функцій, що відповідають програмі ЗНО підготовки з математики.


