Означення, що таке неперервна функція розглядалося раніше. Далі наведено кілька прикладів з дослідження функцій на неперервність, класифікацію точок розриву функцій та показано, як будувати графіки функцій в мейплі.
Приклад 1 Знайти область визначення функції:
2.2.1) 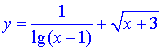
Розв'язання: Область визначення за рахунок логарифма lg(x+1) в знаменнику дробової функції та кореневої sqrt(x+3) ділиться на інтервали на яких функція неперервна.
Точки між інтервалами визначаємо з наступних міркувань:
І) Підлогарифмічний вираз завжди повинен бути більший нуля, тобто
x-1>0,
ІІ) Знаменник дробу не повинен дорівнювати нулю, тому логарифм не рівний нулю
log(x-1)<>0.
ІІІ) Підкореневий вираз має бути невід'ємний, тобто
x+3>=0.
Об'єднавши всі три умови, знайдемо область визначення заданої функції:
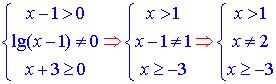
Отже, маємо два інтервали де неперервність функції встановлена:
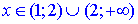
В двійці маємо розрив функції другого роду, оскільки границі справа та зліва прямують до безмежності.
Побудуємо графік функції разом з вертикальною асимптотою в Мейпл.
Для цього запишемо наступний код
> restart;
> with(plots):
> y:=1/log(x-1)+sqrt(x+3);
> q1:=plot(y,x=1..2,color=blue, thickness=2):
> q2:=plot(y,x=2..4,color=blue, thickness=2):
> q3:=plot([[2,-40],[2,20]],color=red, thickness=1):
> display(q1,q2,q3);
Після компіляції отримаємо наступне зображення
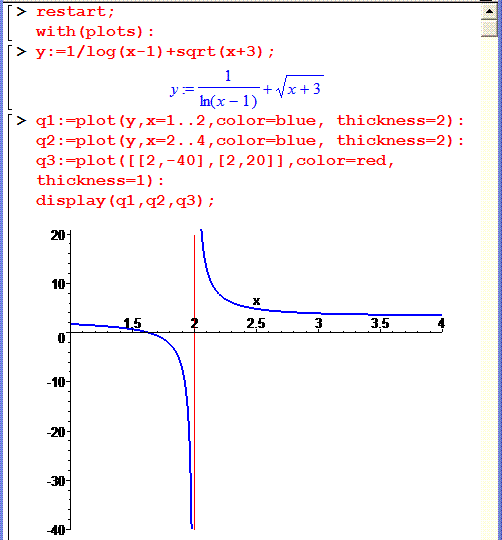
Приклад 2Дослідити функцію на неперервність. Побудувати схематичний графік функції
2.2.2) y=(x+3)/(3x+1).
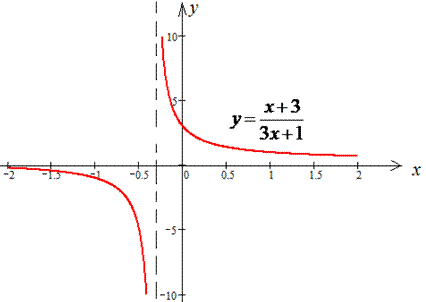
Розв'язання: Оскільки маємо дробову функцію (графіком якої є гіпербола), то розриви функція матиме в точках, де знаменник дорівнює нулю, тобто x0=-1/3.
Отже,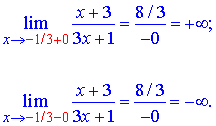
В точці x0=-1/3 задана функція має розрив другого роду. В усіх інших точках функція неперервна.
Приклад 3 Провести дослідження функції на неперервність.
Виконати побудову графіка
2.2.3) 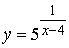
Розв'язання: Оскільки в показнику маємо дробову функцію, то розриви функція матиме в точках, де знаменник дорівнює нулю, тобто x0=4. Отже, 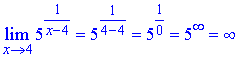
В точці x0=4 задана функція має розрив другого роду.
В усіх інших точках функція неперервна, бо неперервна сама показникова функція.
Графік кусково-неперервної функції зображено на рисунку
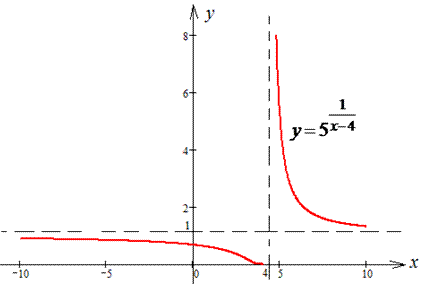
Приклад 4Знайти розри та інтерваи неперервності функції
2.2.4) 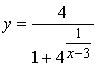
Розв'язання: Розриви функція матиме в точках, де знаменник дорівнює нулю, тобто x0=3, а також
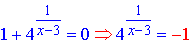
але значення показникової функції повинно бути більше нуля, тому перевірятимемо розрив тільки в точці x0=3.
Отже,
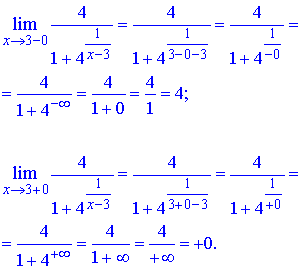
В точці x0=3 задана функція має розрив першого роду – «стрибок». Величина стрибка рівна різниці границь справа та зліва від точки
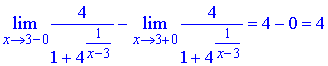
В усіх інших точках функція неперервна.
Тут враховували, що в граничному переході доданок прямує до нуля
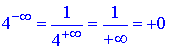
График заданої функції разом з вертикальною та горизонтальною асимптотами наведено далі
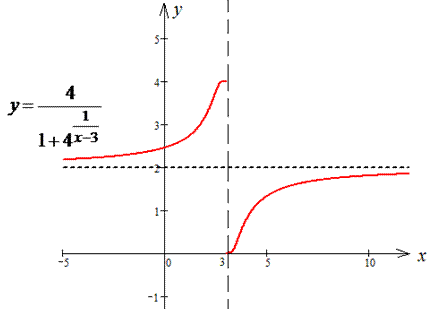
Приклад 5Провести дослідження функції на неперервність. Вказати точки розриву та їх характер
2.2.5) 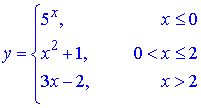
Розв'язання: З візуального перегляду ф-ї бачимо, що на неперервність слід перевіряти функцію на границі інтервалів. Для кращого її уявлення покажемо спершу її графік
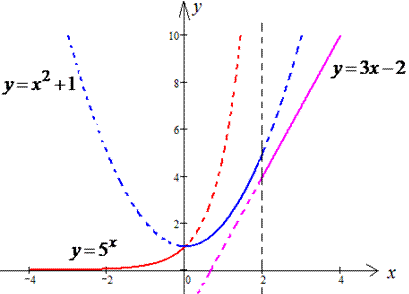
Суцільною лінією позначено криві на тих проміжках, де функція визначена за умовою. Як було зауважено на початку, показникова y=5x, квадратична y=x2+1 і лінійна y=3x-2 функції є неперервними на всій своїй області визначення.
Тому на розриви будемо досліджувати в точках x1=0 і x2=2.
Односторонні границі справа та зліва нуля рівні одиниці
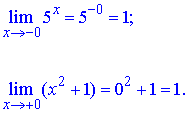
Оскільки значення границь співпадають та скінченні
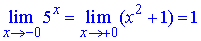
то в точці x1=0 функція неперервна.
Знайдемо границі справа та зліва від точки x2=2
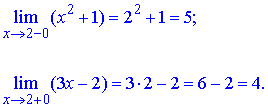
Односторонні границі приймають різні значення
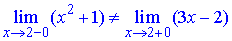
тому в точці x2=2 функція має розрив першого роду – «стрибок».
Величина стрибка функції рівна різниці односторонніх границь:
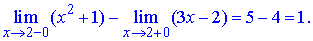
Подібний графік не важко побудувати в Мейпл, дя цього Вам стане в нагоді наступний код
restart;
> with(plots):q1:=plot(5^x,x=-4..0,color=red, thickness=2):
> q2:=plot(x^2+1,x=0..2,color=blue, thickness=2):
> q3:=plot(3*x-2,x=2..4,color=violet, thickness=2):
> display(q1,q2,q3);
В результаті на екрані отримаємо наступний комбінований графік функції
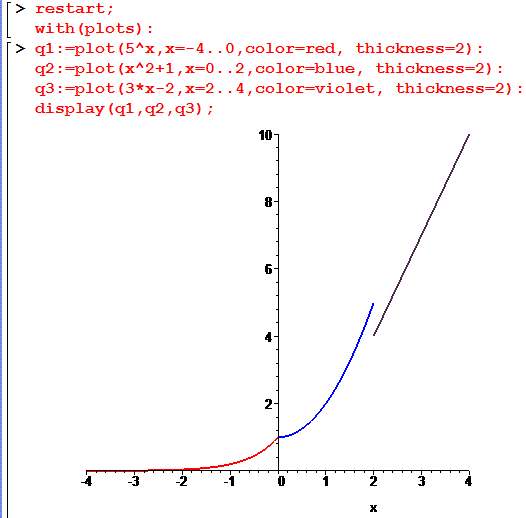
Границі функцій, які тут знаходили також не важко визначити в Мейплі, але про це піде мова в наступних статтях.
Дослідженню неперервності функцій присвячено чимало статтей, в першу чергу перегляньте ті де виконується повне дослідження функції.


