В попередній статті дані означення похилих, вертикальних, горизонтальних асимптот. Зараз же будуть наведені приклади знаходження асимптот із застосуванням правила Лопіталя. Його зручно застосовувати при знаходженні границь з невизначеностями типу нуль розділити на нуль (0/0) чи безмежність розділити на безмежність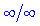 
, тобто, коли маємо границю вигляду
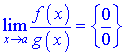
або
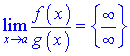то за правилом Лопіталя її значення рівне
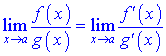якщо функції диференційовні і визначені в околі точки x=a. Похідну можна застосовувати повторно до тих пір, поки не отримаємо константу в чисельнику чи знаменнику, або дріб позбудеться особливості.
Знаходження похилих асимптот. Правило Лопіталя розкриття границь
Приклади. Знайти асимптоти ліній
І .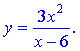 
Розв'язання: Знаменник дробу не повинен перетворюватися в нуль
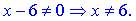
Звідси робимо висново, що область визначення складатимеся з двох інтервалів
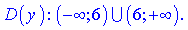
Точка, яка розбиває область визначення буде вертикальною асимптотою x=6. Знайдемо похилу асимптоту
y=kx+b.
Першу невідому (k) знайдемо з границі
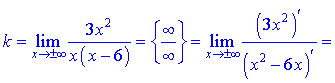
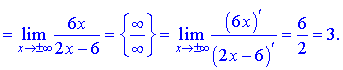
Другу визначаємо за правилом
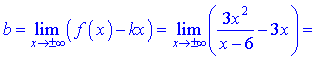
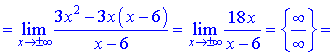
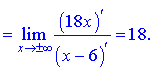
Остаточне рівняння похилої асимптоти наступне
y=3x+18.
Функцію з асимптою зображено графічно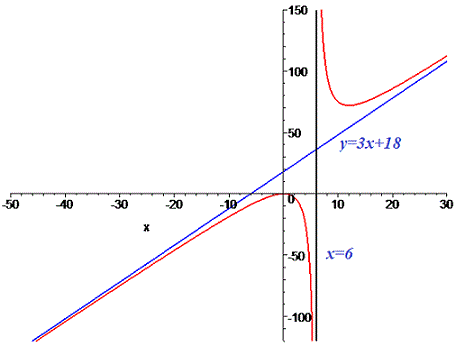
ІІ.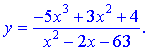 
Розв'язання: Добова функція визначена в усіх точках крім тих, в яких знаменник рівний нулю. Знайдемо розв'язки квадратного рівняння
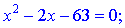
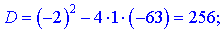
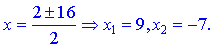
Обидва корені розбивають область визначення на три інтервали
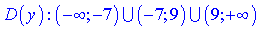
а також є вертикальними асимптотами функції. Похилу асимптоту знаходимо із застосуванням правила Лопіталя
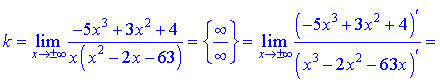
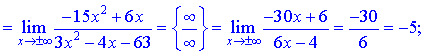
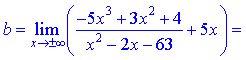
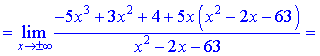
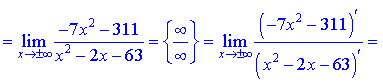
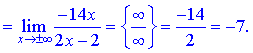
При обчисленні констант k, b, що входять в рівняння прямої, довелося застосувати правило Лопіталя тричі для першого та двічі для другого коефіцієнта. В кінцевому результаті отримали рівняння похилої асимтпоти
y=x-7.
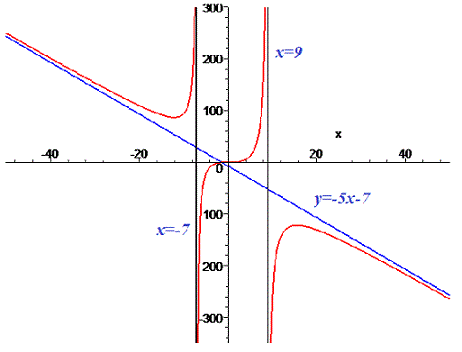
Графік функції з асимптотами має наступний вигляд
III.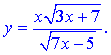 
Розв'язання: З вигляду дробової ірраціональної функції слідує, що вона визначена в усіх точках де визначені корені як чисельника, так і знаменника
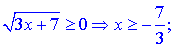
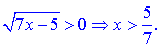
Накладаючи обидва проміжки отримаємо область визначення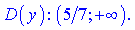 
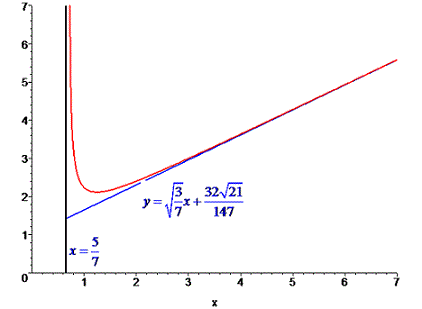
Точка x=5/7 є вертикальною асимптотою функції. Обчислимо коефіцієнти, що входять в рівняння похилої асимптоти. Застосування правила Лопіталя до даного прикладу ніяких спрощень не дасть, тому винесемо домінуючі множники з коренів та знайдемо границі
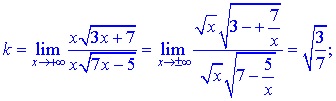
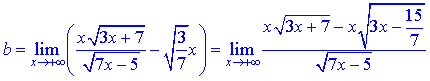
Спростимо вираз в чисельнику
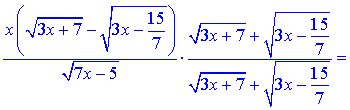
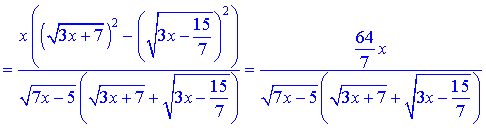
та підставимо в границю
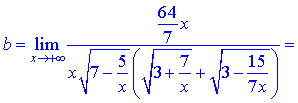
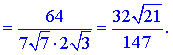
Обчислення границь в цьому завданні зайняло доволі багато часу.
Рівняння похилої асимптоти
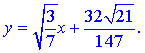
Графік заданої функції з похилою асимптотою наступний
Наведені розв'язки лише частково ознайомили Вас з можливими прикладами, які можуть чекати Вас на практиці. Для кращого володіння даною тематикою розв'язуйте завдання самостійно, вивчайте зручні методики знаходження границь, які дозволять отримати результати швидко.
