Продовжуємо вивчати основні геометричні перетворення функції і сьогодні розглянемо нові відповіді із ЗНО підготовки з математики на паралельне перенесення графіку функції, симетричне відображення відносно осей, розтяг та стиск до осей графіків функцій. З цього уроку Ви навчитеся складати рівняння функцій за виглядом графіків, а також за графіками прогнозувати, які перетворення графіків простих функцій необхідно виконати.
Для початку трохи повторимо теорію, щоб Ви завжди мали під рукою схеми для розв'язування задач.
Геометричні перетворення графіків функцій
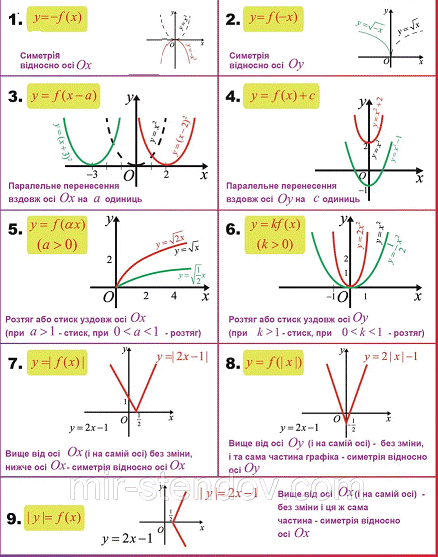
Для побудови графіків функцій Вам необхідно вивчити наступну таблицю з ескізами графіків, щоб знати що робити з функцією у=f(x) :
у=-f(x);у=f(-x);у=f(x)+b;у=f(x+a);у=af(x);у=f(ax);у=f(|x|);у=|f(x)|;|у|=f(x).
Для Вас підготовлено понад 30 готових завдань, тому якщо наступні приклади Вам важкі для розуміння, що і для чого робили, просимо почати вивчати тему геометричних перетворень графіків функцій з уроків, опублікованих раніше. Повірте, що на ЗНО тестах Вас можуть чекати як аналогічні тести, так і значно складніші завдання.
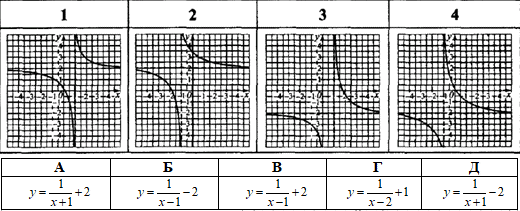
Приклад 23.19 На якому з рисунків зображено графік функції y=(x-1)/(x-2)?
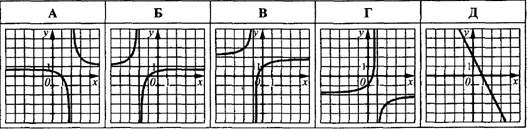
Розв'язування: Зробимо деякі алгебраїчні перетворення виразу:
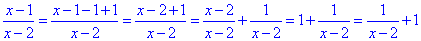
Отримали, y=1/(x-2)+1.
Графік функції y=1/x (гіперболу) зсунули праворуч на 2 одиниці, отримаємо y=1/(x-2).
Графік функції y=1/(x-2) зсунули на 1 одиницю вгору, отримаємо y=1/(x-2)+1.
На рисунку перетворення від першої до кінцевої функції мають вигляд
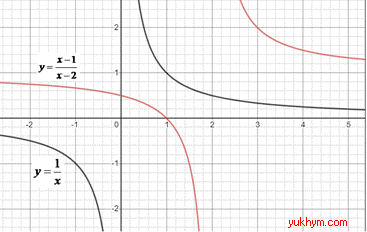
Порівнюючи робимо висновок, що графік функції y=(x-1)/(x-2) зображений на рисунку А.
Відповідь: А.
Приклад 23.3 Указати формулу функції, графік якої отримують із графіка y=cos(x) у результаті його стискування до осі Ox утричі.
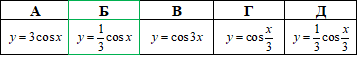
Розв'язування: Графік функції y=c•f(x) можна одержати із графіка функції y=f(x) за допомогою розтягу від осі Ox у c разів, якщо c>1, і за допомогою стиснення до осі Ox у c разів, якщо 0<c<1.
Стиснення це зменшення, тому с=1/3. Побудуємо косинусоїду за умовою прикладу.
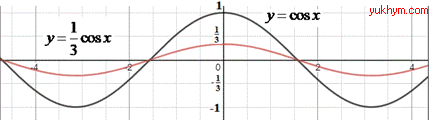
З графіка функції y=cos(x), у результаті його стиснення до осі Ox у тричі, отримаємо функцію y=cos(x)/3.
Відповідь: y=co(x)/3 – Б.
Якщо потрібно розтягнути (0<k<1) або стиснути (k<1) у k разів графік функції до осі Oy тоді слід використовувати правило 5 таблиці y=f(k•x).
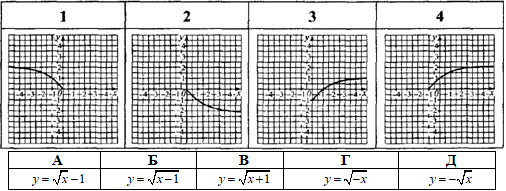
Приклад 23.20 Ескіз графіка якої з наведених функцій зображено на рисунку?
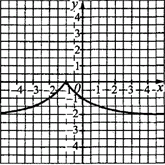
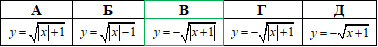
Розв'язування: Візьмемо кореневу функцію y=√x (крива, яка має початок в точці (0;0)). На заданому ескізі графіка функція має лише від’ємні значення (тому y=-√x); симетрично відображена відносно осі Oy (тому y=-√|x|);
має початок у точці (-1;0) (отримаємо паралельним перенесенням графіка y=-√|x| на 1 одиницю ліворуч).
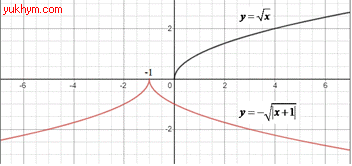
Отримали y=-√|x+1| варант В тестів.
Самостйно розберіться та вивчіть таблицю з основними геометричними перетвореннями, щоб також розуміти, які зміщення на шо впливають та як при цьому змінюються рівняння кривих.
Відповідь: y=-√|x+1| – В.
Приклад 23.29 Установити відповідність між геометричними перетвореннями графіка функції y=cos(x) (1–4) та функціями, одержаних у результаті цих перетворень (А–Д).
1. Графік функції y=cos(x) симетрично відобразили відносно осі Ox 2. Графік функції y=cos(x) симетрично відобразили відносно осі Oy 3. Частину графіка функції y=cos(x), яка лежить вище від осі Ox і на 4. Першу частину графіка функції y=cos(x), яка лежить праворуч від | А. y=|cos(x)| Б. y=|cos(|x|)| В. y=cos|x| Г. y=cos(-x) Д. y=-cos(x) |
Розв'язування: 1. Графік функції y=cos(x) симетрично відобразили відносно осі Ox, отримаємо графік функції y=-cos(x). 1 – Д.
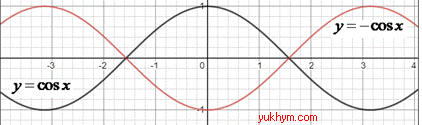
2. Графік функції y=cos(x) симетрично відобразили відносно осі Oy, отримаємо графік функції y=cos(-x). 2 – Г.
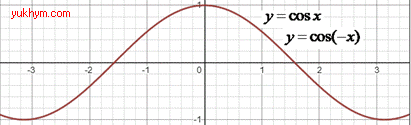
3. Частину графіка функції y=cos(x), яка лежить вище від осі Ox і на самій осі, залишили без змін, а частину, яка лежить нижче від осі Ox, відобразили симетрично відносно цієї осі, отримаємо графік функції y=|cos(x)|. 3 – А.
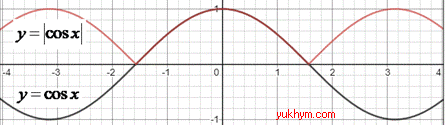
4. Першу частину графіка функції y=cos(x), яка лежить праворуч від осі Oy і на самій осі, залишили без змін, а другу частину замінили симетричною до першої відносно осі Oy, отримаємо графік функції y=cos|x|. 4 – В.
Приклад 23.30 Установити відповідність між графіками функцій (1–4) та їх формулами (А–Д).
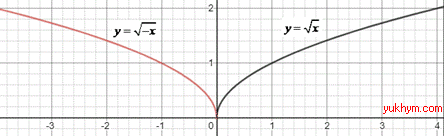
Розв'язування: 1. Графік кореневої функції y=√x симетрично відобразили відносно осі Oy, отримаємо графік функції y=√(-x). 1 – Г.
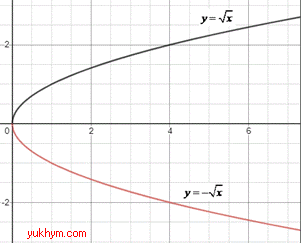
2. Графік кореня y=√x симетрично відобразили відносно осі Ox, отримаємо графік функції y=-√x. 2 – Д.
3. Кореневу функції y=√x посунули на 1 одиницю вниз, отримаємо графік функції y=√x-1. 3 – А.
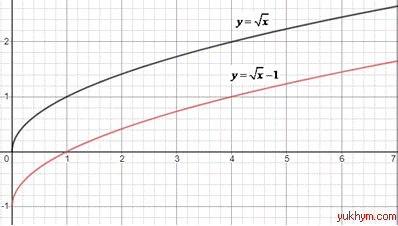
4. Графік функції y=√x посунули на 1 одиницю ліворуч, в результаті отримали графік y=√(x+1). 4 – В.
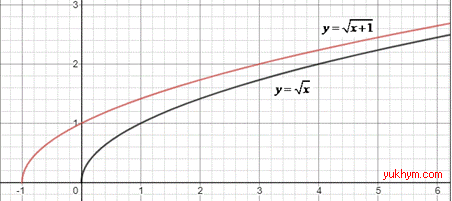
Приклад 23.31 Установити відповідність між графіками функцій (1–4), утворених із графіка функції y=1/x, та їх формулами (А–Д).
Розв'язування: 1. Графік функції y=1/x паралельно перенесли праворуч на 1 одиницю та паралельно перенесли вгору на 2 одиниці, отримаємо графік функції y=1/(x-1)+2. 1 – В.
На рисунку це має вигляд:
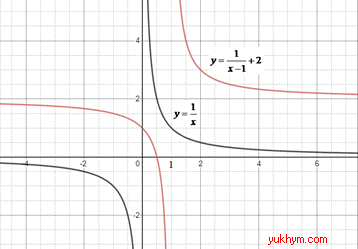
2. Графік функції y=1/x паралельно перенесли ліворуч на 1 одиницю та паралельно перенесли вгору на 2 одиниці, отримаємо графік функції y=1/(x+1)+2. 2 – А.
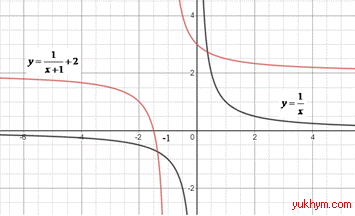
3. Графік функції y=1/x паралельно перенесли праворуч на 1 одиницю та паралельно перенесли вниз на 2 одиниці, отримаємо графік функції y=1/(x-1)-2. 3 – Б.
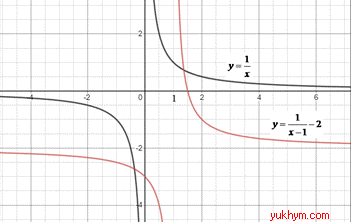
4. Графік функції y=1/x паралельно перенесли ліворуч на 1 одиницю та паралельно перенесли вниз на 2 одиниці, отримаємо графік функції y=1/(x+1)-2. 4 – Д.
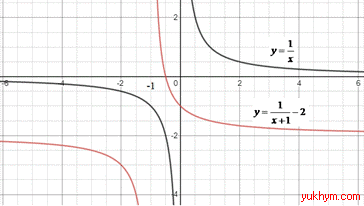
Приклад 23.32 Установити відповідність між ескізами графіків функцій (1–4), утворених із графіка функції y=|x|, та відповідними формулами (А–Д).
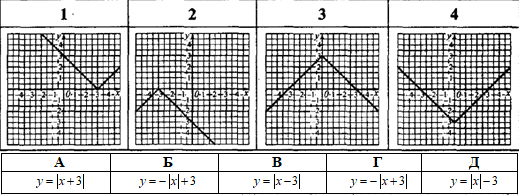
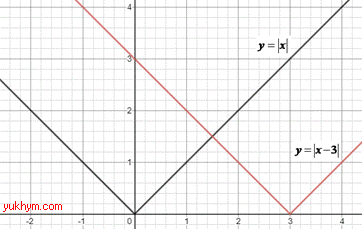
Розв'язування: 1. Графік функції y=|x| паралельно перенесли праворуч на 3 одиниці, отримаємо графік функції
y=|x-3|. 1 – В.
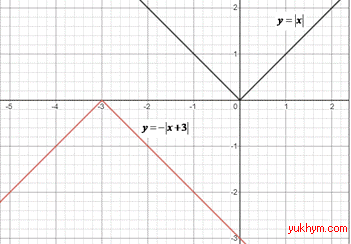
2. Графік функції y=|x| паралельно перенесли ліворуч на 3 одиниці та симетрично відобразили відносно осі Ox, отримаємо графік функції
y=-|x+3| 2 – Г.
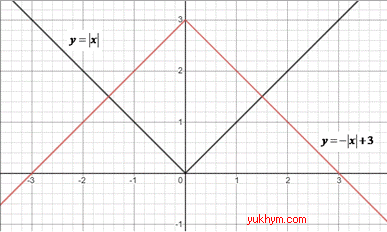
3. Графік функції y=|x| симетрично відобразили відносно осі Ox та паралельно перенесли вгору на 3 одиниці, отримаємо графік функції
y=-|x|+3. 3 – Б.
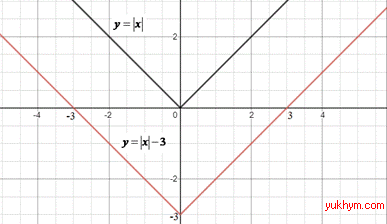
4. Графік функції y=|x| паралельно перенесли вниз на 3 одиниці, отримаємо графік функції
y=|x|-3. 4 – Д.
Наведені приклади на паралельне перенесення графіка функцій вздовж осей, розтяг та стиск, відображення від'ємних або додатних значень в повній мірі повинні підготувати Вас до складання вступних іспитів. Додавайте ресурс в закладки та використовуйте матеріали в шкільній програмі, ЗНО тестах та навчанні у ВУЗах.


