Густина (щільність) розподілу імовірностей. Обчислення та побудова

Для неперервних випадкових величин поряд із законом розподілу ймовірностей розглядають густину (щільність) імовірностей, яку позначають так f(x). Густиною (щільністю) імовірностей неперервної випадкової величини X є перша похідна від інтегральної функції розподілу ймовірностей F(x)

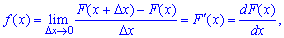
звідки диференціал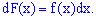
Оскільки приріст визначають залежністю

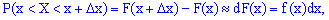
то добуток щільності ймовірностей на приріст випадкової величини f(x)dx відповідає ймовірність того, що випадкова величина X міститиметься у проміжку [x; x+dx], де dx це приріст .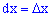
Геометрично на графіку щільності ймовірностей f(x)dx відповідає площа прямокутника з основою dx і висотою f(x)

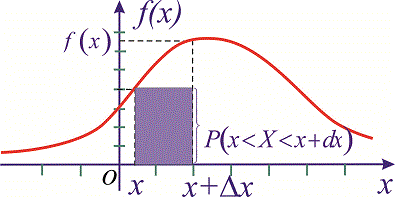
Властивості щільності ймовірностей

1. Щільність ймовірностей приймає додатні значення 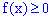. Ця властивість випливає з означення першої похідної від функції розподілу F(x), яка в свою чергу є неспадною функцією.

2. Умова нормування неперервної випадкової величини X

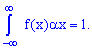
3. Імовірність попадання неперервної випадкової величини в проміжок 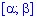визначається залежністю

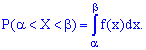
4. Функція розподілу ймовірностей неперервної випадкової величини визначається через щільність розподілу ймовірностей інтегруванням

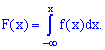
Розглянемо задачі для закріплення матеріалу на практиці.

Приклад 1. Закон розподілу неперервної випадкової величини X задано функцією
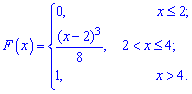
функція розподілу
Знайти щільність розподілу ймовірностей f(x) і побудувати графіки обидвох функцій f(x), F(X). Обчислити ймовірність того, що випадкова величина належить проміжку P(2,5<X<3,5).

Розв'язання.Обчислюємо похідні від закону розподілу X

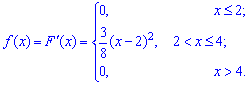
Це і буде щільність розподілу ймовірностей.
Графіки функцій f(x), F(X) зображено на рисунках

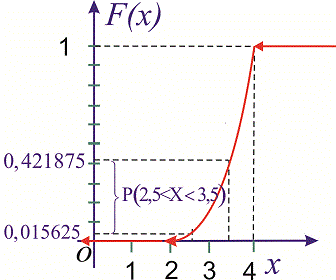
функція розподілу

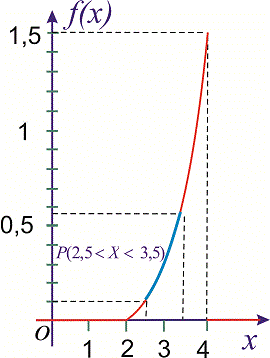
щільність розподілу

Імовірність події 2,5<X<3,5 обчислимо за формулою

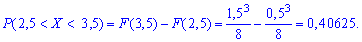
Згідно наведеної вище формули отримаємо
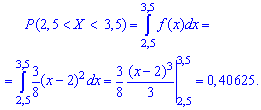
ймовірність попадання в проміжок
Інтегруванням щільності визначили, що ймовірність попадання веичии в проміжок рівна 0,4.

Приклад 2. За заданою функцією щільністі розподілу ймовірностей

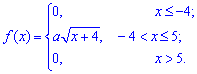
встановити параметр a та функцію розподілу ймовірностей F(x). Побудувати графіки функцій f(x), F(X).

Розв'язання. Значення сталої a визначаємо з умови нормування

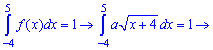
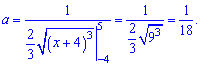
При знайденому значенні a щільність імовірностей матиме вигляд

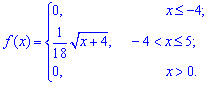
розподіл ймовірностей F(x) визначається інтегруванням щільності:
функція розподілу
Записуємо загальний вигляд функції F(x)

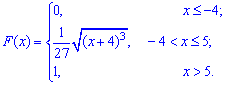
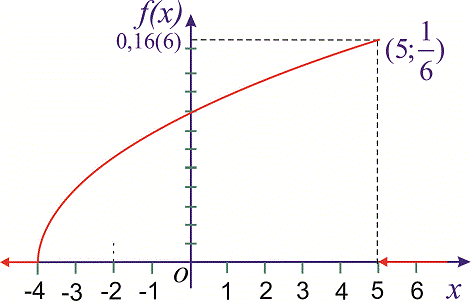
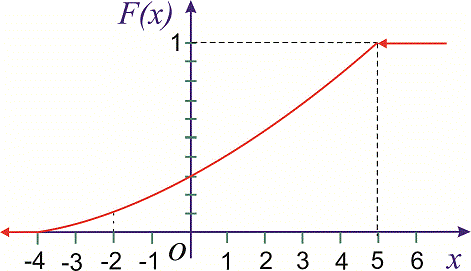
Графіки функцій розподілу ймовірностей та її щільності зображено на рисунках.

щільність розподілу

функція розподілу

Приклад 3. Випадкова величина X має закон розподілу ймовірностей у вигляді трикутника

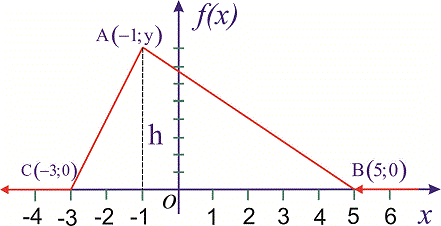
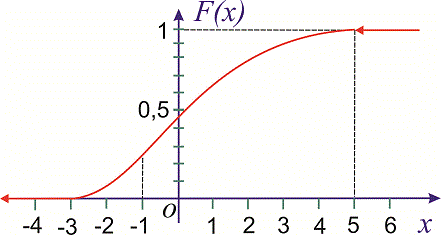
Записати вирази для щільності ймовірностей і функції розподілу ймовірностей, побудувати графік F(x) та обчислити P()<X<3).

Розв'язання. З умови завдання слідує, що щільність імовірностей на проміжках [-3;-1] та [-1;-5] змінюється за лінійним законом вигляду

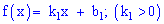
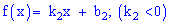
для першої та другої ділянки відповідно. Для знаходження невідомих констант 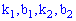встановимо ординати вершини трикутника A(-1; y). Використаємо умову нормування, згідно з якою площа трикутника 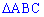рівна одиниці:

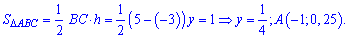
При відомих координатах усіх вершин знаходимо рівняння прямих

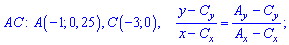
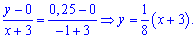
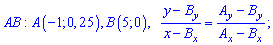
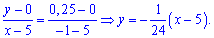
Є інший спосіб знаходження рівняння прямих, який передбачає відшукання по одній константі на рівняння. Якщо відома точка перетину прямої з віссю ординат Ox, то рівняння прямої яка через цю точку проходить наступне

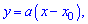
де x₀ – ордината перетину з віссю Ox. Підстановкою другої точки прямої знаходять невідому константу a. Для заданих точок отримаємо

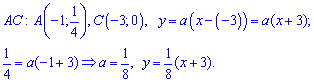
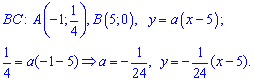
З часом другий метод для Вас стане простішим та практичнішим у використанні Щільність ймовірностей набуде значень

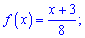
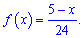
а її функція прийме вигляд

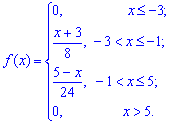
Функцію розподілу ймовірностей F(x) знаходимо інтегруванням:

а) на проміжку [-3;-1]:
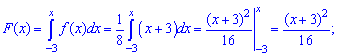
розподіл ймовірностей F(x)
2) на проміжку [-1;5]

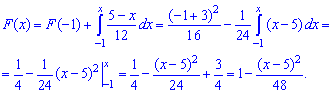
Отже, функція розподілу ймовірностей має вигляд

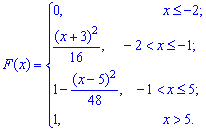
Її графік наведено нижче

Обчислюємо ймовірність події P(0<X<3) згідно формули

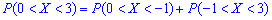
або

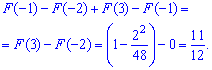
Отже, ймовірність попадання в проміжок рівна

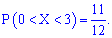
Добре проаналізуйте наведені приклади - це допоможе навчитися швидко знаходити щільність розподілу ймовірностей та виконувати побудову графіка. Будьте уважні при інтегрування та вибирайте зручну для обчислень методику.