Продовжуємо розбирати відповіді до границь. Прикладів назбиралося настільки багато, що можна написати окрему книжку - методичку з їх обчислення.
В кожній публікації розжовуємо методику обчислень до елементарних дрібниць, при таких поясненнях кожен студент може без проблем вирішити подібні приклади.
Проте далі від студентів поступають нові замовлення з просьбою визначити границю.
Часом потрібно допомогти з настільки простими функціями, що сладається враження що студенти мають гіршу підготовку ніж учні в 11 класі, які вивчають цю тему.
Приклад 11. Обчислити границю послідовності:
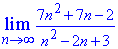
Розв'язання: Підстановка великого номера у послідовність дає особливість типу безмежність розділити на безмежність. Для її розкриття в чисельнику та знаменнику дробу виділяємо доданок, що вносить найбільший вклад. В дужках залишаться константи + доданки, які прямують до нуля.
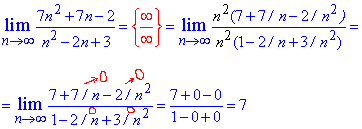
На спільний множник спрощуємо, а сталі дають значення границі послідовності.
Приклад 12. Знайти границю послідовності:
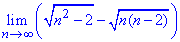
Розв'язання: В граничному переході маємо невизначеність типу безмежність мінус безмежність. Функція представлена різницею коренів. Щоб позбутися невизначеності помножимо та поділимо різницю на суму коренів (спряжений вираз). В результаті прийдемо до невизначеності безмежність поділити на безмежність. Щоб її розкрити виносимо множник, що вносить найбільший вклад з чисельника та знаменника та скорочуємо на нього. Все що залишиться і буде границею послідовності
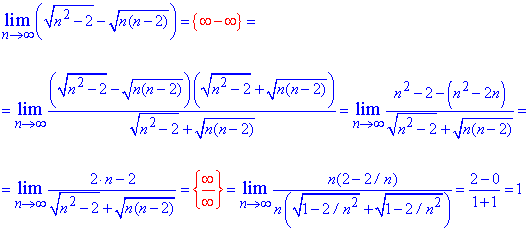
Приклад 13. Знайти границю функції
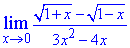
Розв'язання: При змінній прямуючій до нуля маємо невизначеність {0/0}. Для її усуненення різницю коренів домножимо та поділимо на спряжений вираз, щоб в чисельнику утворити різницю квадратів. В знаменнику маємо поліном, який містить особливість, тому розкладемо його на прості множники. Після спрощень отримаємо залежність, границю якої легко знаходимо методом підстановки
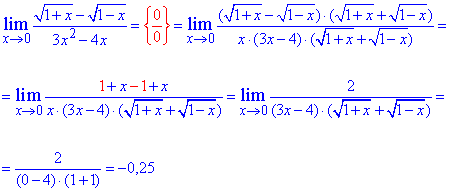
Приклад 14. Обчислити границю
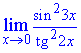
Розв'язання: Змінна прямує до нуля,а функція задана часткою синуса та тангенса в квадраті. В таких випадках потрібно перетворити вираз, щоб в ньому можна було легко виділити першу важливу границю та один з її наслідків. Для компенсації змін в чисельник і знаменник записуємо відповідні сталі. Далі переходимо до добутку відомих границь, вклад від кожної з яких рівний одиниці. 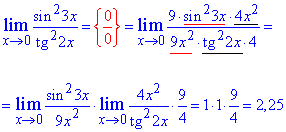
Залишиться стала 9/4, яка і є шуканою границею функції.
Приклад 15. Визначити границю функції
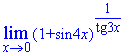
Розв'язання: При ззмінній прямуючій до нуля отримаємо невизначеність типу одиниця в степені безмежності. Для її розкриття виразимо в степені множник,який обернено пропорційний до sin(4x).
Таким чином отримаємо другу важливу границю – експоненту, а все що залишиться в показнику дасть степінь експоненти. Але тут маємо, частку sin(4x)/tan(3x) , тому переходимо до границі в показнику, а сам показник зводимо до першої границі та її наслідку.
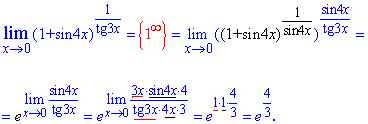
З останнього «ліміту» можна вивести просту формулу, яка може бути розглянута як наслідок першої важливої границі. Границя частки тангенса до синуса (чи навпаки) рівна частці їх аргументів.
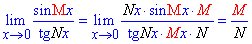
Приклад 16. Знайти границю послідовності:
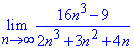
Розв'язання: Для розкриття особливості типу нескінченність розділити на нескінченність потрібно тричі застосувати правило Лопіталя. Інша схема полягає у винесенні з чисельника та знаменника найбільшого множника, та скороченні на нього. В результаті залишаться стала та нескінченно малі функції. Останні прямують до нуля, тому ліміт послідовності рівний
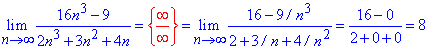
Приклад 17. Обчислити границю послідовності:
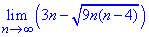
Розв'язання: Таких лімітів в попередніх публікаціях обчислено чимало і суть розкриття подібних невизначеностей полягає у домноженні на спряжений вираз – суму коренів. На цей же вираз слід розділити функцію, щоб не змінити значення ліміту. В результаті в чисельнику дробу отримаємо різницю квадратів і таким чином позбуваємося ірраціональності, а границя виразу що отримаємо визначається через оцінку максимальних множників.
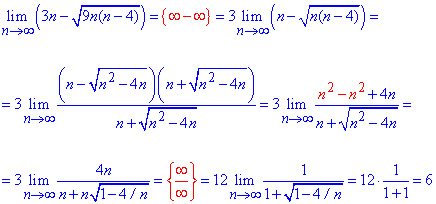
Приклад 18. Визначити границю функції
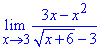
Розв'язання: Коли змінна прямує до трійки отримаємо невизначеність типу {0/0}. Для розкриття невизначеності в знаменнику дробу позбуваємося ірраціональності домноженням на спряжений вираз, а в чисельнику поліном розкладаємо на прості множники. В результаті і тат і там отримуємо вираз (х-3), на який спрощуємо.
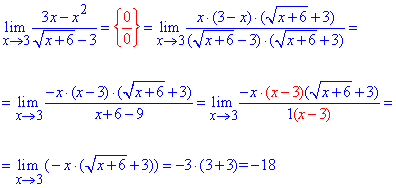
Ліміт функції, що залишилася обчислюємо методом підстановки.
Приклад 19. Знайти границю функції
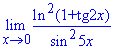
Розв'язання: Границя функції в нулі дає особливість {0/0}. Її не так просто розкривати, як попередні.
Тут слід звести вираз до першої та другої важливих границь та їх наслідків.
Ln(1+x)/x в граничному переході дасть одиницю, так само як і tan(x)/x та sin(x)/x.
Стала 4/25 , що залишиться і буде лімітом функції.
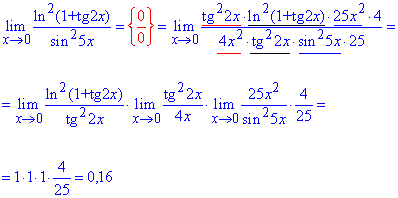
Приклад 20. Знайти границю
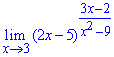
Розв'язання: Границя функції в точці має невизначеність типу одиниця в степені безмежність. Для її розкриття треба перетворити функцію під другу важливу границю. Для цього і в дужках, і в показнику виділяємо множник, що вносить особливість (x-3) та робимо заміну змінних t=x-3.
Далі переходимо до експоненти і визначаємо ліміт показникової функції.
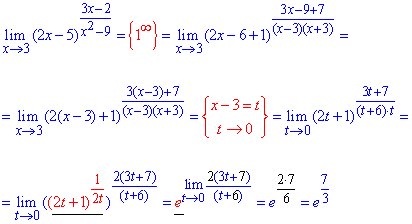
Як Ви могли переконатися, завдання на границі не найважчі в вищій математиці.
Потрібно знати не так багато правил, щоб без труднощів знаходити правильну відповідь.


