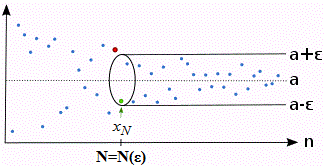
Число a називається границею числової послідовності {xn}, якщо для будь-якого як завгодно малого додатного числа ε>0 знайдеться таке натуральне число N=N(ε), таке що при всіх n>N виконується нерівність |xn-a|<ε.
Якщо a є границею послідовності то цьому відповідає запис
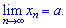
Обчислення границі числової послідовності
Приклад 1 Легке завдання, яке вчить виносити домінантні множники, котрі дають найбільший вклад при номері прямуючому до безмежності, в дробах та спрощувати на них
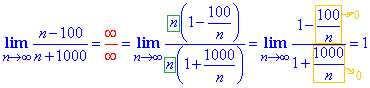
Якщо послідовність збіжна, то вона має скінченну границю. Якщо границя рівна безмежності, то така послідовність є розбіжною.
Для встановлення збіжності послідовностей потрібно добре вміти знаходити границі, що ми з Вами постійно вдосконалюємо.
Приклад 2 Маємо невизначеність виду безмежність мінус безмежність (∞-∞), тому теорему про різницю границь тут застосовувати не можна. Перетворимо вираз, помноженням та діленням на спряжений вираз. Для обчислення значення границі спрощуємо дріб на вираз, що вносить найбільший вклад при аргументі прямуючому до нескінченності. Як виносити множники з пд кореня Ви повинні навчитися самостійно, без цього важко буде розкривати границі з коренями.
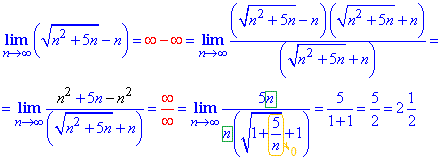
Приклад 3 Різницю коренів в знаменнику дробу не домножуємо на спряжений вираз, а просто номер n виносимо з під кореня (уважно перегляньте як це робити), а далі спрощуємо з n виділеним в чисельнику
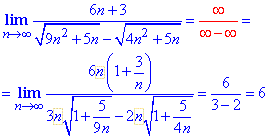
Приклад 4 Послідовність із частки ірраціональних виразів має скінченну границю, якщо степінь номера n в знаменнику рівний степені в чисельнику (або більший). Його виділяємо за вказаною в формулі методикою, та спрощуємо
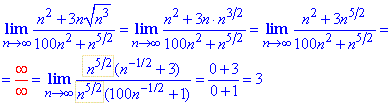
Приклад 5 Знайти границю послідовності 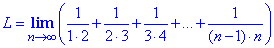
Обчислення: Проаналізувавши, як змінюються доданки для всіх номерів k=2,3,4 можна записати формулу
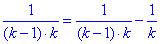
Таким чином вихідну суму зводимо до вигляду
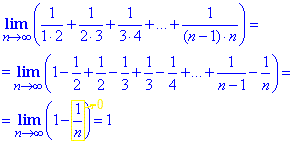
Єдиного усталеного алгоритму, як розкривати такі суми немає. Деколи можна побачити прості схеми чередування доданків, в інших завданнях буває потрібно обчислюваити суми арифметичних чи геометричних прогресій. Лиш би оцінити зверху, що послідовність обмежена, та до якого значення прямує.
Приклад 6 Ліміт послідовності із частки показникових виразів обчислюють шляхом виділення і спрощення домінантних множників в чисельнику та знаменнику дробу. В заданій границі основи рівні 2 та 4, їх можна звести до спільної 4 в (найвищому) степені рівному n. Все решта і дасть значення до якого прямує дріб.
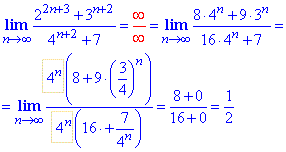
Приклад 7 Границя послідовності з різниці нескінченно великих дробів розкриваємо методом зведення їх до спільного знаменника та спрощення в чисельнику та знаменнику множника, що вносить головний вклад
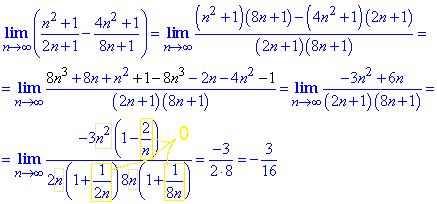
Приклад 8 Знайти ліміт послідовності
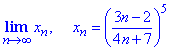
Обчислення: Представимо загальний член послідовності {xn} у вигляді
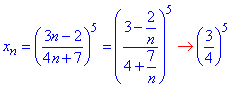
За теоремою про границю показникової функції, вона рівна показнику від границі основи, якщо степінь скінченна. Звідси lim{xn}=(3/4)^5.
Приклад 9 В такого сорту винесення n в найвищому степені за дужки в чисельнику та знаменнику дробу до спрощення не призведе. Спробуйте перевірити самостійно, залишається поглянути в формули скороченого множення та розписати різниці та суми в кубі та четвертому степені за наступними формулами
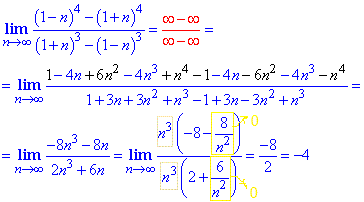
Таким чином отримаємо доданки з протилежними знаками, які в сумі дадуть 0, решта в граничному переході спроститься за наведеною вище методикою.
І наостанок, ще кілька розв'язків на границю послідовності, які пропонуємо розібрати самостійно.
10 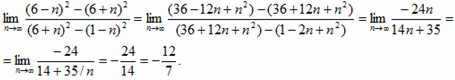
11 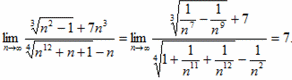
12 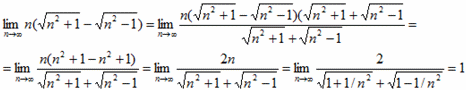
13 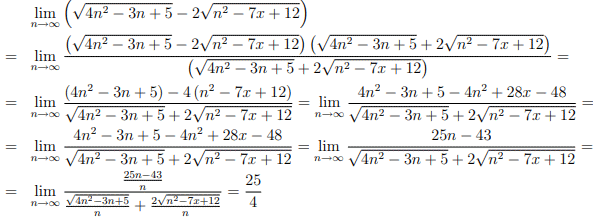
Переглянути подібні матеріали:


